Squeezenet is a CNN architecture which has 50 times less parameters than AlexNet but still maintains AlexNet level accuracy. We also showcased the architecture of the model alongwith the implementation on the ImageNet dataset.

Table of contents:

• Introduction
• Design of the SqueezeNet model
  • Architectural design strategies
  • The Fire Module
  • The SqueezeNet architecture
  • Other details
• Evaluation of SqueezeNet
• Conclusion

Introduction

A significant part of the research on deep convolutional neural networks (CNNs) has zeroed in on expanding precision on computer vision (CV) datasets. For a given metric level, say accuracy, there commonly exist numerous CNN structures that accomplish that level of accuracy. For a given equivalent accuracy, a CNN model with less number of parameters enjoys the following benefits:

1. Increase in efficiency of distributed training
2. Less overhead when sending out new models to customers
3. Feasible FPGA and embedded deployment

1. Increase in efficiency of distributed training.

The restricting component to the scalability of distributed CNN training is the communication among the servers. For a given distributed data-parallel training, communication overhead is directly proportional to the number of parameters in the CNN model. To put it plainly, smaller models has a faster training as they require less communication between the servers.

2. Less overhead when sending out new models to customers.

For self-driving organizations, for example, Tesla intermittently copy the new models from their servers to clients' vehicles. This training is regularly alluded to as an over-the-air update (OTA update). Customer Reports has tracked down that the wellbeing of Tesla's Autopilot semi-autonomous driving usefulness has gradually improved with recent over-the-air updates. Nonetheless, over-the air updates of the present average CNN/DNN models can require enormous information moves. With AlexNet, this would require 240MB of correspondence from the worker to the vehicle. More modest models require less communication, making successive updates more possible.

3. Feasible FPGA and embedded deployment.

FPGAs, or Field-Programmable Gate Array, generally have under 10MB of on-chip memory and no off-chip memory or capacity. For instance, an sufficiently little model could be put away straightforwardly on the FPGA as opposed to being bottlenecked by memory data transmission, while video frames gets transferred through the FPGA continuously. Further, while sending CNNs on Application-Specific Integrated Circuits (ASICs), an sufficiently little model could be put away straightforwardly on-chip, and more smaller models may empower the ASIC to fit on a more smaller die.

Hence, we can see that smaller CNN architectures possess an advantage as they have fewer parameters with equivalent accuracy.

Design of the SqueezeNet model

This section deals with the SqueezeNet model and how it is made to have 50 times less parameters than the state-of-the-art AlexNet model.

Architectural design strategies

SqueezeNet model uses certain strategies to trim the majority of parameters. These are:

1. Replacing the 3x3 filters with 1x1 filters
2. Decreasing the number of input channels to 3x3 filters
3. Downsampling later at the network

1. Replacing the 3x3 filters with 1x1 filters: Due to budget constraints, the model employed the use of 1x1 filters as opposed to the traditional 3x3 filters. Thus the model has 9 times fewer parameters than a traditional filter.

2. Decreasing the number of input channels to 3x3 filters: As the filter size is reduced to 1x1, the number of input channels also needs to be reduced. This is done using the squeeze layer, which will be discussed later.

3. Downsampling later at the network: By downsampling later at the network, we are able to get larger activation maps for the convolution layers. In a convolutional network, each convolution layer produces an output activation map with a spatial resolution that is at least 1x1 and often much larger than 1x1. The height and width of these activation maps are controlled by: (i) the size of the input data (256x256 images) and (ii) the choice of layers in which to downsample in the CNN architecture.

Downsampling is engineered into CNN architectures by setting the (stride > 1) in some of the convolution or pooling layers. If the layers closer to the input layer in the network have large strides, then most layers will have small activation maps. Conversely, if most layers in the network have a stride of 1, and the strides greater than 1 are concentrated toward the end of the network, i.e. closer to the classifier, then many layers in the network will have large activation maps.

Strategies 1 and 2 are mainly to reduce the number of parameters. Strategy 3 is all about maximizing accuracy with the restricted amount of parameters.

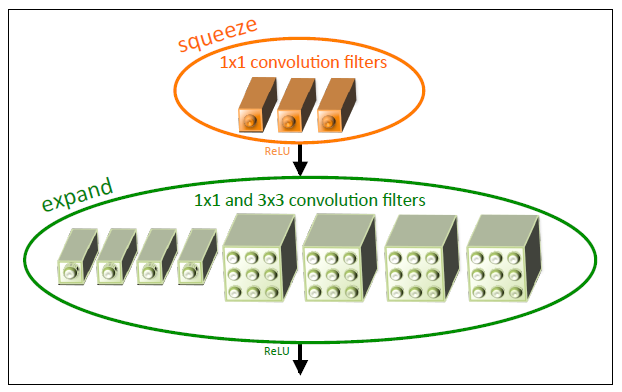
The Fire Module

The Fire module is comprising of a squeeze convolution layer (which has only 1x1 filters), feeding into an expand layer that has a mix of 1x1 and 3x3 convolution filters. The liberal use of 1x1 filters in Fire modules is an application of Strategy 1. We expose three hyperparameters in the Fire module: s1x1, e1x1, and e3x3. In a Fire module, s1x1 is the number of filters in the squeeze layer (all 1x1), e1x1 is the number of 1x1 filters in the expand layer, and e3x3 is the number of 3x3 filters in the expand layer. When we use Fire modules, we set s1x1 to be less than (e1x1 + e3x3), so the squeeze layer helps to limit the number of input channels to the 3x3 filters, as per Strategy 2 mentioned above. Below figure represents the organization of convolution filters in the fire module.

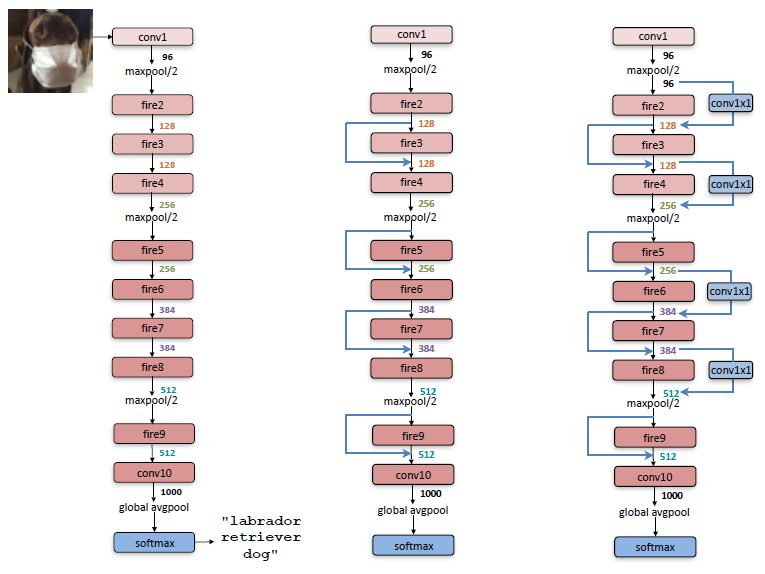
The SqueezeNet architecture

The SqueezeNet architecture begins with a standalone convolution layer (conv1), followed by 8 Fire modules (fire2-9), ending with a final conv layer (conv10). The number of filters per fire module is gradually increased from the beginning to the end of the network. SqueezeNet performs max-pooling with a stride of 2 after layers conv1, fire4, fire8, and conv10; these relatively late placements of pooling are per Strategy 3. The entire macroarchitectural view of the SqueezeNet architecture is showcased below. The leftmost shows SqueezeNet, the middle one is SqueezeNet with simple bypass, and the rightmost one is SqueezeNet with complex bypass.

Other details

• 1-pixel border of zero-padding is added in the input data to 3x3 filters of expand modules. This makes the output activations from 1x1 and 3x3 filters have the same height and width.
• ReLU (rectified linear unit) is the activation function used in the squeeze and expand layers
• Dropout regularization with a ratio of 50% is added after the fire9 module.
• The lack of fully connected layers is inspired by the NiN architecture.
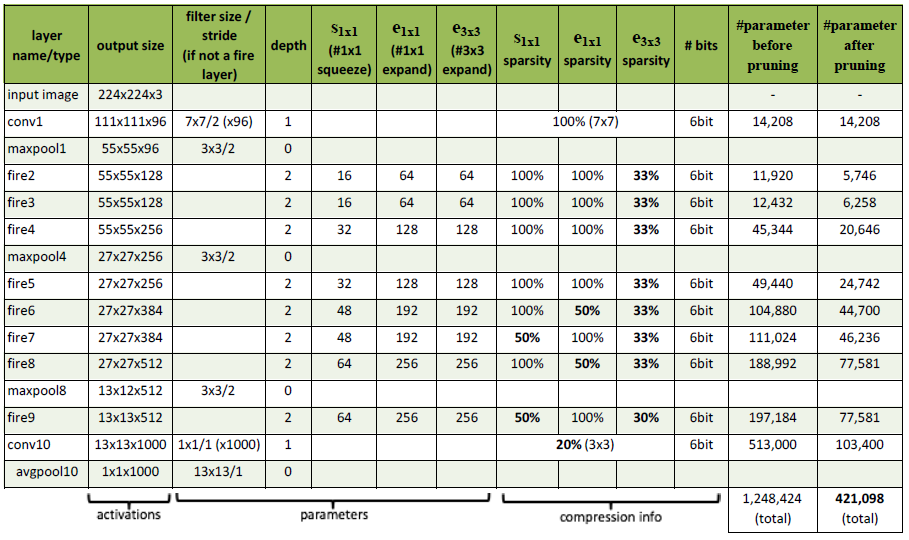
• The learning rate while training SqueezeNet starts with 0.04, and is linearly decreased throughout the training. Refer to this link for details on the training parameters. Below is a figure that comprises of the SqueezeNet architectural dimensions.

Evaluation of SqueezeNet

The model is evaluated on the ImageNet dataset and the output is compared with the output of AlexNet model on the same dataset.

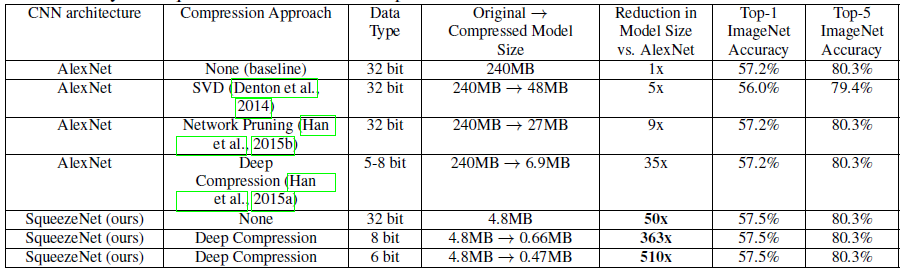
The following table gives us an overview of the various compression techniques used for achieving the highest possible accuracy with fewer parameters.

Following inferences can be made with the above table:

• Pretrained AlexNet model is compressed by a factor of 5x with top-1 accuracy to 56.0% using SVD based approach.
• Network Pruning drives 9x reduction in model size while maintaining the top-1 accuracy and top-5 accuracy on ImageNet.
• Deep Compression drives 35x reduction in model size while maintaining the top-1 accuracy and top-5 accuracy on ImageNet.
• SqueezeNet achieves a 50X reduction in model size compared to AlexNet while maintaining the top-1 accuracy and top-5 accuracy on ImageNet.

Further, 6-bit and 8-bit compression was implemented on the SqueezeNet model making the model down to 0.66 MB and 0.47 MB size respectively (363x and 510x reduction in size respectively) while maintaining the top-1 accuracy and top-5 accuracy on ImageNet.

Conclusion

In this article at OpenGenus, the SqueezeNet model was showcased. Squeezenet is a CNN architecture which has 50 times less parameters than AlexNet but still maintains AlexNet level accuracy. We also showcased the architecture of the model alongwith the implementation on the ImageNet dataset. Also, with the help of deep compression techniques, we are able to fit this model on devices such as FPGAs which have a limited on-chip memory. You can test this model by going to this link.