Find number of substrings with same first and last characters

Problem Statement: You are given a string lets say "S" , you need to find the count/number of all contiguous substrings (part of "S") starting and ending with the same character.

Sample Testcase:

Input : Let S = "abcab"
Substrings can be :

a, ab, abc, abca, abcab, b, bc, bca
bcab, c, ca, cab, a, ab, b

Out of these substrings, ones that have the same first and last characters are-

a, b, c, abca, bcab, a and b.

Explanation - All single-digit have the same first and last characters like a, b and c. Characters that appear multiple times are considered as separate outputs like a and b.

How to approach solution to such a problem:

To come up with a solution to an algorithmic problem, we have to come up with the blueprint of the solution in our mind. What we should think in this case is:

1. To find whether the substrings have the same first and last characters, we have to find all the substrings first.
2. Then, we'll have to compare the first and last elements of every substring and return either the count of the substrings or the exact substrings.

After coming up with a solution, we'll have to come up with a way to code our logic up with any programming language of our choice. We'll choose C/C++ for this problem.

Naive Approach- Pseudocode

#include<header files>
add pre-processor directives

function countSubstrings(string)
    length = length of string
    counter = counts the substrings
    for i in length
        for j in length
            if string[i] equals string[j]
                // means first and last characters are same
                counter++
 
 main()
     s = input string
     call countSubstrings(s);
     end of code

Naive Approach - Code

#include <bits/stdc++.h>  // including all the header files in C++
using namespace std; 

int countSubstrings(string s) 
{ 
    int result = 0;
    // finding the length of the string to iterate through it
    int n = s.length();
  
    // Iterating through all substrings in 
    // way so that we can find first and last 
    // i describes first character
    // j describes last character of the substring
    for (int i=0; i<n; i++) {
        for (int j=i; j<n; j++) {
            // if the first and last character matches, we increase the counter
            if (s[i] == s[j]) {
                result++; 
            }
        }
    }
    // returning the count of the answer
    return result; 
} 
  
// Main function 
int main() {
    string s("abcab"); 
    cout << countSubstrings(s) << endl; // OUTPUT: 7
    return 0; 
}

Example

Input : S = "abac"
Output : 4
The substrings are a, b, a, c and aba.

Complexity Analysis -

The asymptotic complexity is what we'll be analyzing ie, how the complexity of our code grows with the size of our input.
Time Complexity comes out to be O(n^2) and Space Complexity is O(1). By seeing the time complexity, we should understand that there should be a better way to solve this problem. There has to be. (in most cases). How do we know? Because O(n^2) is extremely horrible complexity. For the huge size of data, our code will take years to come up with a solution.

Can we do better?

Of course, we can. If we closely look at the solution, we can understand or at least observe that our answer just depends on the frequencies of characters in the original string. How?

YES, THERE IS! (Permutation and Combination formula)

For example: let strings be "abcab", the frequency of ‘a’ is 2.
Substrings contributing to answer are a, abca and a respectively.
A total of 3.

So, Frequency = 2; Substring = 3

Is there any relation between the frequency and the answer? Using simple permutation and combination which we read in elementary school, we come up with-

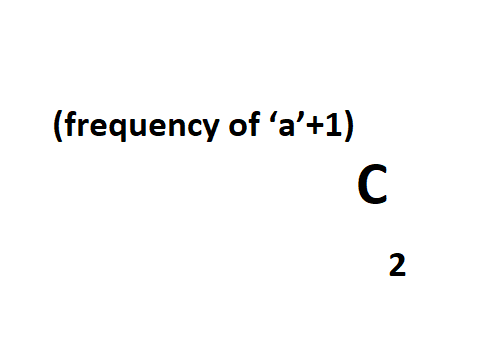
Optimised Approach - Pseudo Code

#include<header files>
add pre-processor directives

function countSubstrings(string)
    length = length of string
    count array = counts the frequency of characters
    for i in length
        marking frequency in count hash table
 
 main()
     s = input string
     using formula to find number of substrings possible
     display the number of substrings
     end of code

Optimised Approach - Code

// Most efficient C++ program to count all   
// substrings with same first and last characters. 
#include <bits/stdc++.h> 
using namespace std; 

int countSubstrings(string s) 
{ 
    int result = 0; 
    int n = s.length();
    // size is 26 because thats the number of characters in English Alphabets
    int count[26] = {0}; 
    // calculating frequency of each character 
    for (int i=0; i<n; i++) {
        count[s[i]-'a']++; 
    }
    
    // Computing result using the frequency table
    for (int i=0; i<26; i++) {
        // using the formula that we built
        result += (count[i]*(count[i]+1)/2); 
    }
    // returning the result
    return result; 
} 
  
// Main function 
int main() {
    string s("abcab"); 
    cout << countSubstrings(s); // OUTPUT: 7
    return 0; 
} 

Complexity Analysis -

We'll again look at the asymptotic complexity of our solution. We are looping through the array of characters or the string once so the time Complexity comes out to be O(n) and we are using an array to keep track of the frequency of each character but it is constant ie 26, hence the Space Complexity is O(26) or O(1). All constant time and space complexity are written as O(1) because we're concerned with the rate of growth of algorithm.

Can we do even better?

As an Engineer, you should always have a curiosity to do better. After every iteration of your code, your project, your interviews, your projects you should strive to perfect your product or the code you wrote. You must always try to optimize your code to attain better complexity. Here, can we come with better time complexity?, say O(logn) or even O(1) ;)

Unfortunately, we can't. In order to find the frequency, we'll have to at least traverse the string once. So, we can't come up with a better solution in this case but you should always ask that question after every line of code that you write!