
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 45 minutes | Coding time: 15 minutes
A trie, also called digital tree and sometimes radix tree or prefix tree (as they can be searched by prefixes), is a kind of search tree—an ordered tree data structure that is used to store a dynamic set or associative array where the keys are usually strings. Unlike a binary search tree, no node in the tree stores the key associated with that node; instead, its position in the tree defines the key with which it is associated. All the descendants of a node have a common prefix of the string associated with that node, and the root is associated with the empty string. Keys tend to be associated with leaves, though some inner nodes may correspond to keys of interest. Hence, keys are not necessarily associated with every node. For the space-optimized presentation of prefix tree, see compact prefix tree.
A Trie is a special data structure used to store strings that can be visualized like a graph. It consists of nodes and edges.
- Each node consists of at max 26 children and edges connect each parent node to its children.
- These 26 pointers are nothing but pointers for each of the 26 letters of the English alphabet A separate edge is maintained for every edge.
- Strings are stored in a top to bottom manner on the basis of their prefix in a trie.
- All prefixes of length 1 are stored at until level 1.
- All prefixes of length 2 are sorted at until level 2 and so on.
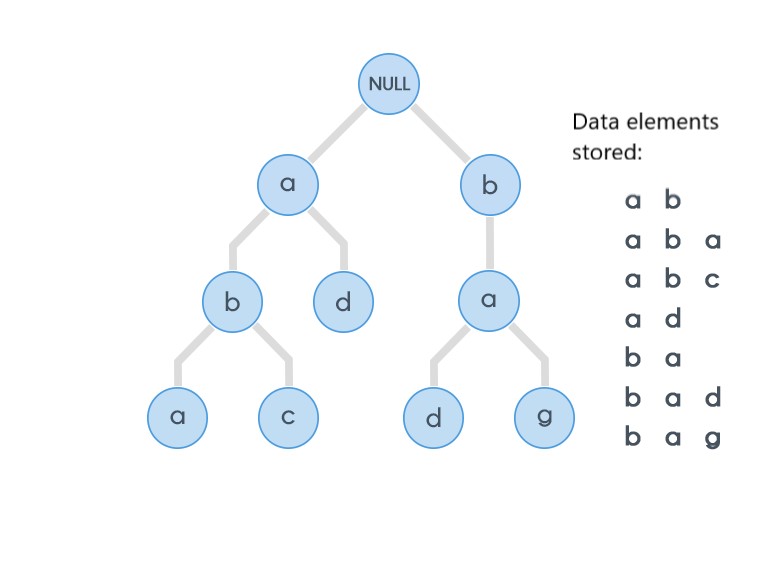
The figure depicts the basic structure of Trie.
Algorithm
Basic operations associated with Trie:
-
Insertion of node in Trie:
- Every character of input key is inserted as an individual Trie node. Note that the children is an array of pointers (or references) to next level trie nodes.
- The key character acts as an index into the array children.
- If the input key is new or an extension of existing key, we need to construct non-existing nodes of the key, and mark end of word for last node.
- If the input key is prefix of existing key in Trie, we simply mark the last node of key as end of word.
- The key length determines Trie depth.
-
Searching a node in Trie
- Searching for a key is similar to insert operation, however we only compare the characters and move down.
- The search can terminate due to end of string or lack of key in trie.
- In the former case, if the isEndofWord field of last node is true, then the key exists in trie.
- In the second case, the search terminates without examining all the characters of key, since the key is not present in trie.
-
Deletion of a node in Trie:
When the current node that we are looking at is not the last node for key 'k', then
1. We first make a recursive call to delete the node which is child of the currentNode.
2. We check if child node was deleted in step #1. If child node was not deleted then child node must be shared with some other key which implies this currentNode is also part of some other key and hence we do not delete currentNode and return deletedSelf = false to the parent node.
3. After step #1, if child node was deleted then we check if this currentNode can be deleted. We check that using two conditions: (a) If this node is marked as a leaf node then this node must be the last node corresponding to some other key and hence we return deletedSelf = false without deleting currentNode. (b) If this node has any more children then that means this node is part of some other key as well and hence return deletedSelf = false without deleting currentNode. (c) If both conditions (a) and (b) evaluate to false then we know that this node can be safely deleted. We return deletedSelf = true by marking currentNode as nullWhen we make currentNode = null for deleting the current node, current node won't be deleted since we are making only the local reference to the node as null. Note that this node still has got another reference in terms of parent node's child reference. To delete the node completely, what we do is once a child returns deletedSelf as true, we make child reference = null as well. Code for this is code snippet is - if (childDeleted) currentNode.children[getIndex(key.charAt(level))] = null;
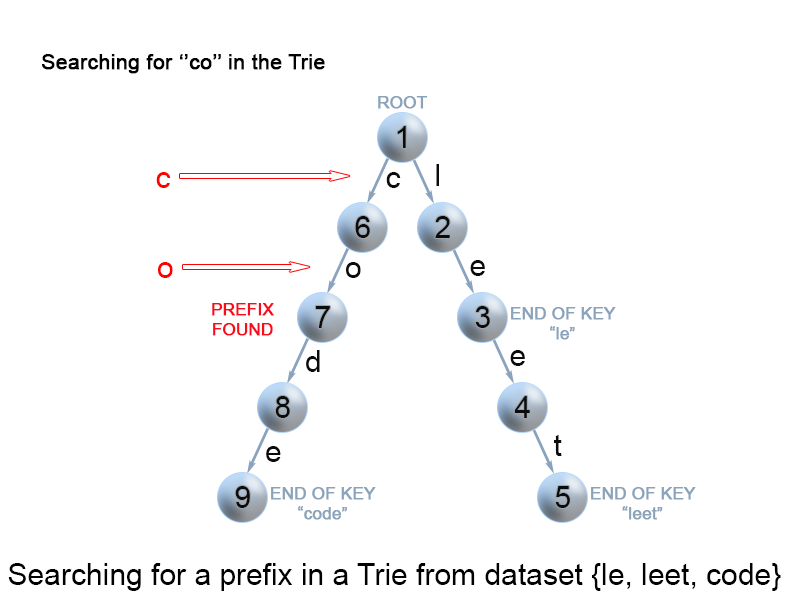
The figure depicts the searching of an element in a Trie.
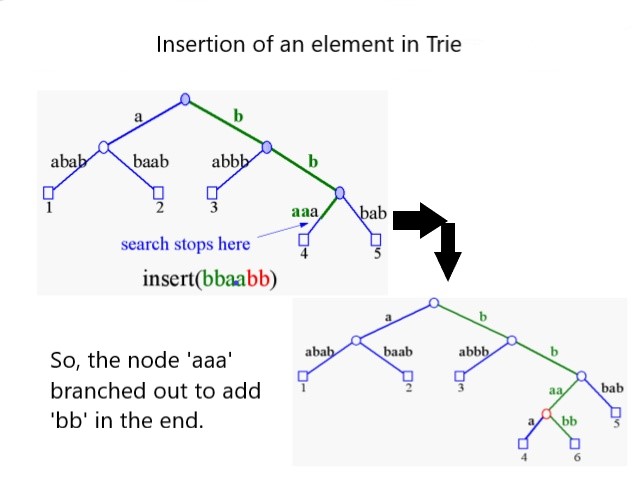
**The figure illustrates the insertion of an element in a Trie.**
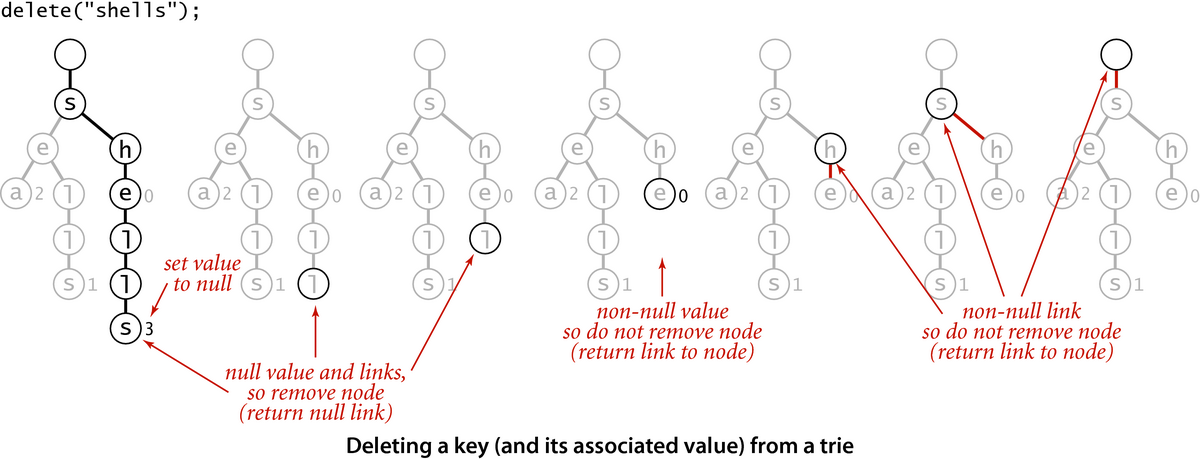
The figure illustrates the deletion of an element from a Trie.
Complexity
-
Worst case search time complexity:
Θ(key_length) -
Average case search time complexity:
Θ(key_length) -
Best case search time complexity:
Θ(1) -
Worst case insertion time complexity:
Θ(key_length) -
Worst case deletion time complexity:
Θ(key_length) -
Worst case Space complexity:
Θ(ALPHABET_SIZE * key_length * Number_of_keys)
Pseudocode
Searching
boolean search(String s)
{
for(every char in String s)
{
if(child node is null)
{
return false;
}
}
return true;
}
Insertion
void insert(String s)
{
for(every char in string s)
{
if(child node belonging to current char is null)
{
child node=new Node();
}
current_node=child_node;
}
}
Deletion
1) If key 'k' is not present in trie, then we should not modify trie in any way.
2) If key 'k' is not a prefix nor a suffix of any other key and nodes of key 'k' are not part of any other key then:
all the nodes starting from root node(excluding root node) to leaf node of key 'k' should be deleted.
3) If key 'k' is a prefix of some other key, then
leaf node corresponding to key 'k' should be marked as 'not a leaf node'. No node should be deleted in this case.
4) If key 'k' is a suffix of some other key 'k1', then:
all nodes of key 'k' which are not part of key 'k1' should be deleted.
5) If key 'k' is not a prefix nor a suffix of any other key but some nodes of key 'k' are shared with some other key 'k1', then:
nodes of key 'k' which are not common to any other key should be deleted and shared nodes should be kept intact.
Implementations
- C++
C++
#include <iostream>
// define character size
#define CHAR_SIZE 128
// A Class representing a Trie node
class Trie
{
public:
bool isLeaf;
Trie* character[CHAR_SIZE];
// Constructor
Trie()
{
this->isLeaf = false;
for (int i = 0; i < CHAR_SIZE; i++)
this->character[i] = nullptr;
}
void insert(std::string);
bool deletion(Trie*&, std::string);
bool search(std::string);
bool haveChildren(Trie const*);
};
// Iterative function to insert a key in the Trie
void Trie::insert(std::string key)
{
// start from root node
Trie* curr = this;
for (int i = 0; i < key.length(); i++)
{
// create a new node if path doesn't exists
if (curr->character[key[i]] == nullptr)
curr->character[key[i]] = new Trie();
// go to next node
curr = curr->character[key[i]];
}
// mark current node as leaf
curr->isLeaf = true;
}
// Iterative function to search a key in Trie. It returns true
// if the key is found in the Trie, else it returns false
bool Trie::search(std::string key)
{
// return false if Trie is empty
if (this == nullptr)
return false;
Trie* curr = this;
for (int i = 0; i < key.length(); i++)
{
// go to next node
curr = curr->character[key[i]];
// if string is invalid (reached end of path in Trie)
if (curr == nullptr)
return false;
}
// if current node is a leaf and we have reached the
// end of the string, return true
return curr->isLeaf;
}
// returns true if given node has any children
bool Trie::haveChildren(Trie const* curr)
{
for (int i = 0; i < CHAR_SIZE; i++)
if (curr->character[i])
return true; // child found
return false;
}
// Recursive function to delete a key in the Trie
bool Trie::deletion(Trie*& curr, std::string key)
{
// return if Trie is empty
if (curr == nullptr)
return false;
// if we have not reached the end of the key
if (key.length())
{
// recurse for the node corresponding to next character in the key
// and if it returns true, delete current node (if it is non-leaf)
if (curr != nullptr &&
curr->character[key[0]] != nullptr &&
deletion(curr->character[key[0]], key.substr(1)) &&
curr->isLeaf == false)
{
if (!haveChildren(curr))
{
delete curr;
curr = nullptr;
return true;
}
else {
return false;
}
}
}
// if we have reached the end of the key
if (key.length() == 0 && curr->isLeaf)
{
// if current node is a leaf node and don't have any children
if (!haveChildren(curr))
{
// delete current node
delete curr;
curr = nullptr;
// delete non-leaf parent nodes
return true;
}
// if current node is a leaf node and have children
else
{
// mark current node as non-leaf node (DON'T DELETE IT)
curr->isLeaf = false;
// don't delete its parent nodes
return false;
}
}
return false;
}
// C++ implementation of Trie Data Structure - Insertion, Searching and Deletion
int main()
{
Trie* head = new Trie();
head->insert("hello");
std::cout << head->search("hello") << " "; // print 1
head->insert("helloworld");
std::cout << head->search("helloworld") << " "; // print 1
std::cout << head->search("helll") << " "; // print 0 (Not found)
head->insert("hell");
std::cout << head->search("hell") << " "; // print 1
head->insert("h");
std::cout << head->search("h"); // print 1
std::cout << std::endl;
head->deletion(head, "hello");
std::cout << head->search("hello") << " "; // print 0 ("hello" deleted)
std::cout << head->search("helloworld") << " "; // print 1
std::cout << head->search("hell"); // print 1
std::cout << std::endl;
head->deletion(head, "h");
std::cout << head->search("h") << " "; // print 0 ("h" deleted)
std::cout << head->search("hell") << " "; // print 1
std::cout << head->search("helloworld"); // print 1
std::cout << std::endl;
head->deletion(head, "helloworld");
std::cout << head->search("helloworld") << " "; // print 0 ("helloworld" deleted)
std::cout << head->search("hell") << " "; // print 1
head->deletion(head, "hell");
std::cout << head->search("hell"); // print 0
std::cout << std::endl;
if (head == nullptr)
std::cout << "Trie empty!!\n"; // Trie is empty now
std::cout << head->search("hell"); // print 0
return 0;
}
Applications
Importance of Trie:
-
There are no collisions of different keys in a trie.
-
Buckets in a trie, which are analogous to hash table buckets that store key collisions, are necessary only if a single key is associated with more than one value.
-
There is no need to provide a hash function or to change hash functions as more keys are added to a trie.
-
A trie can provide an alphabetical ordering of the entries by key.
