
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes
Loss function is an important part in artificial neural networks, which is used to measure the inconsistency between predicted value (^y) and actual label (y). It is a non-negative value, where the robustness of model increases along with the decrease of the value of loss function.
At its core, a loss function is incredibly simple: it’s a method of evaluating how well your algorithm models your dataset. If your predictions are totally off, your loss function will output a higher number. If they’re pretty good, it’ll output a lower number. As you change pieces of your algorithm to try and improve your model, your loss function will tell you if you’re getting anywhere.
Function of loss function?
In mathematical optimization, statistics, econometrics, decision theory, machine learning and computational neuroscience, a loss function or cost function is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event.
In other words the loss function is how you're penalizing your output for predicting wrong output.
Types of loss function
- mean_squared_error
- mean_absolute_error
- mean_absolute_percentage_error
- mean_squared_logarithmic_error
- squared_hinge
- hinge
- categorical_hinge
- logcosh
- categorical_crossentropy
- sparse_categorical_crossentropy
- binary_crossentropy
- kullback_leibler_divergence
- poisson
- cosine_proximity
How to use loss function in your Model
There are variety of pakages which surropt these loss function. Keras is one of them.
In Keras a loss function is one of the two parameters required to compile a model.
y_true : Actual value of label
y_pred : Predicted value of label by the model
This is how you can import loss function in Keras framework:
1. mean_squared_error
keras.losses.mean_squared_error(y_true, y_pred)
In statistics, the mean squared error (MSE) or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and what is estimated.
Y : Actual value
Y^ : Predicted value
n : Number of data point
2. mean_absolute_error
keras.losses.mean_absolute_error(y_true, y_pred)
In statistics, mean absolute error (MAE) is a measure of difference between two continuous variables
yi : Actual value
xi : Predicted Value
3. mean_absolute_percentage_error
keras.losses.mean_absolute_percentage_error(y_true, y_pred)
The mean absolute percentage error (MAPE), also known as mean absolute percentage deviation (MAPD), is a measure of prediction accuracy of a forecasting method in statistics, for example in trend estimation, also used as a Loss function for regression problems in Machine Learning. It usually expresses accuracy as a percentage, and is defined by the formula:
where At is the actual value and Ft is the forecast value. The difference between At and Ft is divided by the actual value At again. The absolute value in this calculation is summed for every forecasted point in time and divided by the number of fitted points n. Multiplying by 100% makes it a percentage error.
4. mean_squared_logarithmic_error
keras.losses.mean_squared_logarithmic_error(y_true, y_pred)

5. squared_hinge
keras.losses.squared_hinge(y_true, y_pred)
6. hinge
keras.losses.hinge(y_true, y_pred)
The hinge loss provides a relatively tight, convex upper bound on the 0–1 indicator function. In addition, the empirical risk minimization of this loss is equivalent to the classical formulation for support vector machines (SVMs). Correctly classified points lying outside the margin boundaries of the support vectors are not penalized, whereas points within the margin boundaries or on the wrong side of the hyperplane are penalized in a linear fashion compared to their distance from the correct boundary.
y : value to be classified
7. categorical_hinge
keras.losses.categorical_hinge(y_true, y_pred)
8. logcosh
keras.losses.logcosh(y_true, y_pred)
9. categorical_crossentropy
keras.losses.categorical_crossentropy(y_true, y_pred)
In information theory, the cross entropy between two probability distributions p and q over the same underlying set of events measures the average number of bits needed to identify an event drawn from the set, if a coding scheme is used that is optimized for an "artificial" probability distribution q, rather than the "true" distribution p.
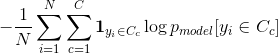
N : Numer of datasets
C : Total number of Classes
pmodel : Probabilit predicted by the model for the ith observation to belong to the cth category
10. sparse_categorical_crossentropy
keras.losses.sparse_categorical_crossentropy(y_true, y_pred)
11. binary_crossentropy
keras.losses.binary_crossentropy(y_true, y_pred)
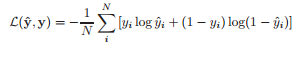
Y : Actual Value
Y^ : Predicted Value
N : Total number of datapoints.
12. kullback_leibler_divergence
keras.losses.kullback_leibler_divergence(y_true, y_pred)
Dkl : Notation of Kullback leibler divergence
In other words, it is the expectation of the logarithmic difference between the probabilities P and Q, where the expectation is taken using the probabilities P. The Kullback–Leibler divergence is defined only if for all x, Q(x)=0 Q(x)=0 implies P(x)=0 P(x)=0 (absolute continuity). Whenever P(x) is zero the contribution of the corresponding term is interpreted as zero
13. poisson
keras.losses.poisson(y_true, y_pred)
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant rate and independently of the time since the last event.
14. cosine_proximity
keras.losses.cosine_proximity(y_true, y_pred)







