In this article we are going to talk about a very interesting problem which is frequently asked in coding interviews and programming competitions - the Word Break Problem.

We have solved the Word Break problem using:

• Recursive approach
• Dynamic Programming [O(N^2) time, O(N^2) space]

Problem Statement

In the problem we are given a string S and a dictionary of words,we have to determine whether S can be segmented into non-empty substrings of one or more dictionary words.(The words need not be unique)

Eg: S = "applepenpie"
dict = {"apple","pen","pie"}
Output : True
We can see that S can segmented into apple,pie and pen all of which belongs to our dictionary

Eg: S = "catsandog"
dict = {"cat","sand","dog"}
Output : False
We can see that the string has cat sand and dog as a substring but on partitioning our condition is not met as they overlap.

Let's think

For better performance and time complexity we will first store all the given words in an unordered_set in C++ or HashSet in Java. This will help us to compare our segments to words efficiently.

If some of you guessed it , you guessed it right. This is a classic partitioning DP Problem. But first we are going to write a recursive solution to the problem.

Method 1 : Recursive Solution

Since we have to partition our the given string we will use 2 pointer approach to mark the beginning and end of our segment.The idea is to divide the string into two parts and try all possible,if a match is found in the first half then check for the second half.

Pseudo Code

    bool wordBreak(s,start,end,dict)
    if(substring in dict){
        return true;
    }
    for(int i=0;i<end;i++){
        if(wordBreak(s,start,i,dict) is true and 
        wordBreak(s,i+1,end) is true){
            return true
    }
    return false;

Recursive Solution Code:

bool wordBreak(string s,int start,int end,unordered_set<string> &dict){
    if(dict.count(s.substr(start,end-start+1))){
        return true;
    }
    for(int i=start;i<end;i++){
        if(wordBreak(s,start,i,dict) && wordBreak(s,i+1,end,dict)){
            return true;
        }
    }
    return false;
}

In the above C++ code we are running a loop from start to end in which we partition a string into two parts first from start to i and the other from i+1 to end.Initially start = 0 and end = S.length - 1. In each iteration we are recursively checking the segments until a match is found or we return false.

Solution Analysis

The above code does our job but the above solution is very costly. Let's see first we are running a loop and in each iteration we are recursively calling two functions. This clearly indicates that our code is of exponential time complexity.For large inputs of string the recursive solution proves to be costly.One thing to note is that we have overlapping subproblems in this recursion and we are calling same recursive funcions several times. This will be the most important factor for our optimization.

Method 2 : Dynamic Programming

We can use Dynamic Programming Approach to optimize our recursive solution.In Dynamic Programming we use a data strucutre to store our results from recursive solutions to avoid repetitive recursive calls. For more details on DP check out the OpenGenus DP articles.

Introduction to Dynamic Programming
Dynamic Programming Questions

Algorithm

First we are going to talk about DP array.

1. DP Array
   • We create a 2D Array of size nxn where n is the size of the string
   • We then initialize all the elements of the DP array with 0. Each element DPi,j in the array contains a boolean value if substring s[i:j] is present in the dict or not
2. Recursive Calls
   • We first check if the given substring is present in the dict
   • If yes, we mark the substring in DP array (DP[i][start])return true else we proceed
   • Else we run a loop from the starting index of the substring to the ending index of the substring. If the substring in the iteration is marked we return the stored value else we enter the recursive call and store the result
   • We recursively try to partition each substring in the words present in the dict
   • The two partitions in each iteration is s[start:i] and s[i+1:end] if both are present in the dict we got our answer we mark dp[i][start] and d[i+1][end] according to the recursive call
   • Else we return false,continuing our recursive calls ulimately returning false as we there is no answer.

Pseudo Code

    bool wordBreak(s,start,end,dict){
        if(substring of s in dict){
            dp[start][end] = 1;
            return true;
        }
        for(int i=start;i<end;i++){
            if(dp[i][start] marked){
                return dp[i][start];
            }else{
                dp[i][start] = wordBreak(s,start,i,dict);
                if(dp[i][start] is true){
                    dp[i+1][end] = wordBreak(s,i+1,end)
                    if(dp[i+1][end] is true){
                        return true;
                    }
                }
            }
        }
        dp[start][end] = 0;
        return false;
    }

Memoization Solution

Memoization or Top-Down approach is a widely used DP optimizing method. Here we pass an additional data strucuture and check wheter we already have the answer to this segment ,if not we calculate it recursively and store the result in the data structure. We generally us an array. The dimensions of the array depends on the parameters changing in our recurisve functions.In our case two parameters are changing (start and end) therefore we will use a 2D Array or vector in C++ STL.

Solution Code

bool wordB(string s,int start,int end,unordered_set<string> &dict,vector<vector<int>> &dp){
    if(dict.count(s.substr(start,end-start+1))){
        dp[start][end] = 1;
        return true;
    }
    for(int i=start;i<end;i++){
        if(dp[start][i] == -1){
            dp[start][i] = wordB(s,start,i,dict,dp);
        }
        if(dp[start][i]){
            dp[i+1][end] = wordB(s,i+1,end,dict,dp);
            if(dp[start][i] && dp[i+1][end]){
                return true;
            }
        }
    }
    dp[start][end] = 0;
    return false;
}
int main(){
    string s;
    cout << "Enter the string : ";
    cin >> s;
    unordered_set<string> dict;
    int x;
    cout << "Enter the number of strings in the dictionary : ";
    cin >> x;
    cout << "Enter the strings in the dictionary : ";
    for(int i=0;i<x;i++){
        string arg;
        cin >> arg;
        dict.insert(arg);
    }
    bool wb = wordBreak(s,0,s.length(),dict);
    if(wb){
        cout << "The string can be partitioned into one or more strings in the dictionary\n";
    }else{
        cout << "The string cannot be partitioned into one or more strings in the dictionary\n";
    }
    return 0;
}

Example Walkthrough

Let's walkthrough a simple example to get better understanding of our code.
Assume
S = "ironman"
dict = {"iron","man"}
Since length of the string is 7, therefore our DP array will be 7x7 2D array.start = 0 and end = 7
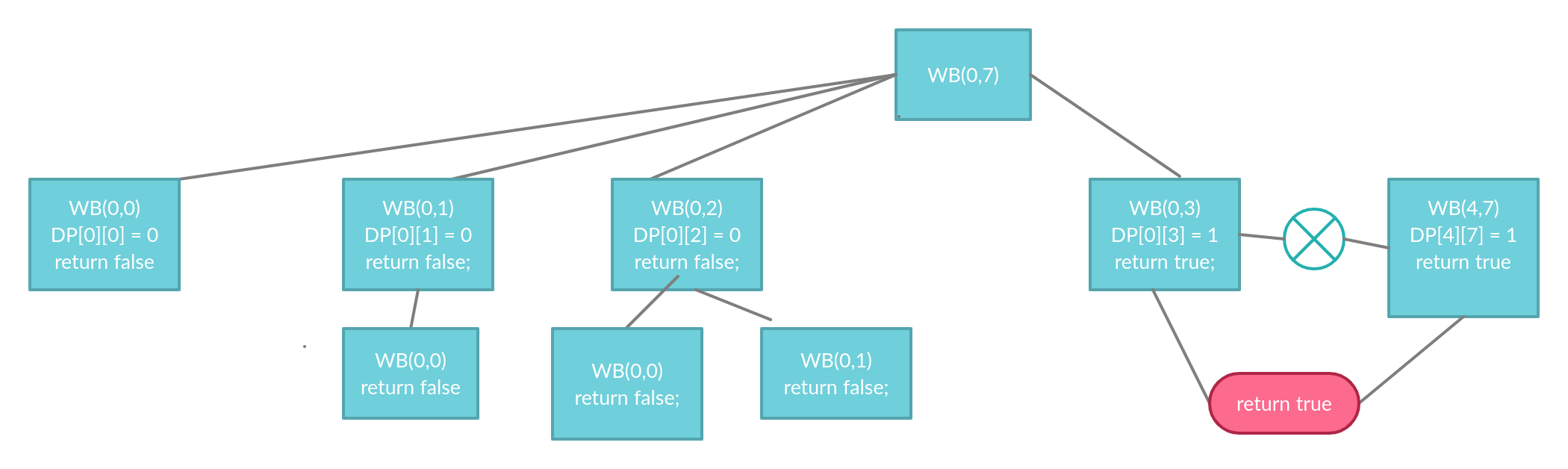
To understand better let us ignore dict and dp array and abbreiviate our recursive funcition by WB(i,j) where i = start and j = end

We start with WB(0,7)

First iteration(i = 0)

As we can see we will start matching the second half only when we find a match in the first half

We call WB(0,0)

As we can see "i" does not belong to the dict therefore we continue and since start == end therefore we don't even enter the loop and return false
DP[0][0] = 0

Second Iteration(i = 1)

We call WB(0,1)

Since "ir" is not in the dict we continue and this function will call WB(0,0) which is already computed.
DP[0][1] = 0
We return false

Third Iteration(i = 2)

We call WB(0,2)

Since "iro" is not in the dict we continue and call WB(0,0) and WB(0,1)
DP[0][2] = 0
We return false

Fourth Iteration(i = 3)

We call WB(0,3)

Since "iron" is in the dict we immediately return true and since our match is found therefore we proceed to second half
DP[0][3] = 1

We call WB(4,7)

Since "man" is in the dict we return true. Since both our conditions are met
DP[4][7] = 1
We return True and our function call ends.

You can refer to the below tree diagram for reference :

Sample I/O and O/P

    Enter the string : ironman
    Enter the number of strings in the dictionary : 2
    Enter the string in dictionaries: iron man
    The string can be partitioned into one or more strings in the dictionary

Solution Analysis

You can see the code is almost the same for recursive and memoization solution.The only difference being we pass and additional 2D array dp of size nxn where n is the size of the string.dp[i][j] stores a boolean value whether a substring starting with i and ending with j is present in the dict or not.

We initialize our 2D array with a value which cannot be a possible solution say -1.We first check whether we already have calculated the result or not by checking if dp[start][end] == -1. If yes we simply return the result else we call our recursive function and store the recursive calls in the corresponding dp[i][j].

This drastically improves out solution's time. Since there are nxn slots in our dp array and each fills exactly once our optimized time complexity is O(N^2) which is a lot better than the original exponential one.

Conclusion

In this article we saw how DP can optimize exponential time recursive solutions to polynomial time solutions. Talking about auxiliary space we store our results in a nxn 2D array. Therefore auxiliary space is also O(N^2).