Reading time: 35 minutes

We are given with a valid sentence without any spaces and we are given with a dictionary of words. We need to print all the possible ways to break the sentence so that all the breaked words belongs to the dictionary.

For Example:

dictionary: {i, hello, mango, man,go, how, ice, cream, like, cell}
Input: "icelikemango"
Output: "ice like man go"
        "ice like mango"
"So the input can be breaked into to meaningful sentences"

Here we will see two approachs to implement the solution for this problem, one is Backtracking approach and the other is Trie building approach.

Algorithms

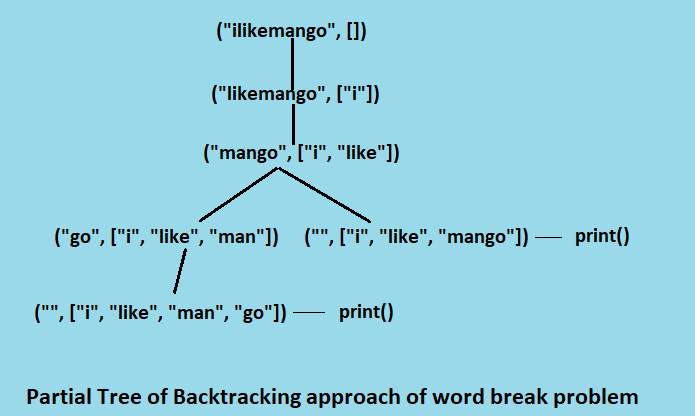
1. Backtracking approach

In this approach we start scanning the sentence from left. As we find a valid word, we need to check whether rest of the sentence can make valid words or not. Because in some situations the first found word from left side can leave a remaining portion which is not further separable. So in that case we should backtrack and leave the current found word and keep on searching for the next word. To keep track of the found words we will use the stack overhead. Whenever the right portion(suffix) of the string does not make valid words, we backtrack and pop the top string from stack and continue finding.

def word_breaks(string, sentc=list()):
    n = len(string)
    if n == 0:
        print(" ".join(i for i in sentc))
        return
    for i in range(1, n + 1):
        if dictionary.__contains__(string[0: i]):
            word_breaks(string[i:], sentc=sentc+[string[0: i]])

The above method recursively checks, if the dictionary contains prefix then it recurs for the suffix of the string. When the lenght of the string becomes zero, then we print the current sentence segment.
The backtracking approach takes O(2ⁿ*s) time as there are total 2ⁿcombinations are possible for the string and we we match it with the dictionary words of max lenght s.

2. Trie Search approach

In this method we build a trie structure from the given dictionary words. Instead
of searching the word in the dictionary we search it it the trie as it would take lesser time to search. But as a whole we apply the same backtracking approach to find the word breaks so overall time taken by the algorithm is O(2ⁿ * s).

def search(text, trie):
    text += '$'
    node = 0
    for c in text:
        if node in trie:
            if c in trie[node]:
                node = trie[node][c]
            else:
                return False
        else:
            return False
    return True

def word_breaks(string, sentc=list(), trie=dict()):
    n = len(string)
    if n == 0:
        print(" ".join(i for i in sentc))
        return
    for i in range(1, n + 1):
        if search(string[0: i], trie):
            word_breaks(string[i:], sentc=sentc+[string[0: i]], trie=trie)

Implementation

Code in python3

Backtracking Approach

dictionary = ['i', 'like', 'mango', 'man', 'go', 'book', 'design',
            'code', 'eat', 'ice', 'icecream', 'cream']
def word_breaks(string, sentc=list()):
    n = len(string)
    if n == 0:
        print(" ".join(i for i in sentc))
        return
    for i in range(1, n + 1):
        if dictionary.__contains__(string[0: i]):
            word_breaks(string[i:], sentc=sentc+[string[0: i]])

print("Possible word breaks are:")
word_breaks("ilikemango")

Output

Possible word breaks are:
i like man go
i like mango

Trie search Approach

dictionary = ['i', 'like', 'mango', 'man', 'go', 'book', 'design',
              'code', 'eat', 'ice', 'icecream', 'cream']

def build_trie(patterns):
	tree = dict()
	keys = 1
	for pattern in patterns:
		node = 0
		pattern += '$'
		for c in pattern:
			if node in tree:
				if c in tree[node]:
					node = tree[node][c]
				else:
					tree[node].update({c: keys})
					node = keys
					keys += 1
			else:
				tree[node] = {c: keys}
				node = keys
				keys += 1
	return tree

def search(text, trie):
    text += '$'
    node = 0
    for c in text:
        if node in trie:
            if c in trie[node]:
                node = trie[node][c]
            else:
                return False
        else:
            return False
    return True

def word_breaks(string, sentc=list(), trie=dict()):
    n = len(string)
    if n == 0:
        print(" ".join(i for i in sentc))
        return
    for i in range(1, n + 1):
        if search(string[0: i], trie):
            word_breaks(string[i:], sentc=sentc+[string[0: i]], trie=trie)

trie = build_trie(dictionary)
print("Possible word breaks are")
word_breaks(string="icelikeicecream", trie=trie)

Output

Possible word breaks are:
ice like ice cream
ice like icecream

Complexcity

Time Complexity

• Time Complexity of Both approach is O(2ⁿ) in the worst case.

Space Complexity

• Space complexity of Backtracking approach is O(n).
• Space complexity of Trie approach is O(m /* s + n), where m is the length of dictionary.