Bernoulli Naive Bayes is a variant of Naive Bayes. So, let us first talk about Naive Bayes in brief. Naive Bayes is a classification algorithm of Machine Learning based on Bayes theorem which gives the likelihood of occurrence of the event. Naive Bayes classifier is a probabilistic classifier which means that given an input, it predicts the probability of the input being classified for all the classes. It is also called conditional probability.

Two important assumptions made for Naive Bayes Classifier:

• First is that the attributes are independent of each other and does not affect each others performance, this is the reason it is called 'naive'.
• Second is that all the features are given equal importance. For example if there are 10 features, knowing only 5 features will not give us accurate outcome. All features are necessary to predict outcome and are given equal importance.

Bayes theorem is as follows:

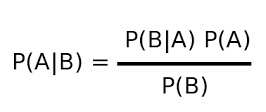
where,
P(A|B) = Probability of A given evidence B has already occurred
P(B|A) = Probability of B given evidence A has already occurred
P(A) = Probability that A will occur
P(B) = Probability that B will occur

Bayes theorem can be used for many real life scenarios like scam detection, credit card fraud detection, disease detection, sentiment analysis and many more.

There are three types of Naive Bayes Classifiers:

1. Multinomial Naive Bayes - Widely used classifier for document classification which keeps the count of frequent words present in the documents.

2. Bernoulli Naive Bayes - Used for discrete data, where features are only in binary form.

3. Gaussian Naive Bayes - Used when we are dealing with continuous data and uses Gaussian distribution..

We will talk about Bernoulli Naive Bayes in detail in this article.

Bernoulli Naive Bayes

This is used for discrete data and it works on Bernoulli distribution. The main feature of Bernoulli Naive Bayes is that it accepts features only as binary values like true or false, yes or no, success or failure, 0 or 1 and so on. So when the feature values are binary we know that we have to use Bernoulli Naive Bayes classifier.

Bernoulli distribution

As we deal with binary values, let's consider 'p' as probability of success and 'q' as probability of failure and q=1-p
For a random variable 'X' in Bernoulli distribution,

where 'x' can have only two values either 0 or 1

Bernoulli Naive Bayes Classifier is based on the following rule:

$$P(x_i\mid y)=P(i\mid y)x_i+(1-P(i\mid y))(1-x_i)$$

Now, let us solve a problem for Bernoulli Naive Bayes:

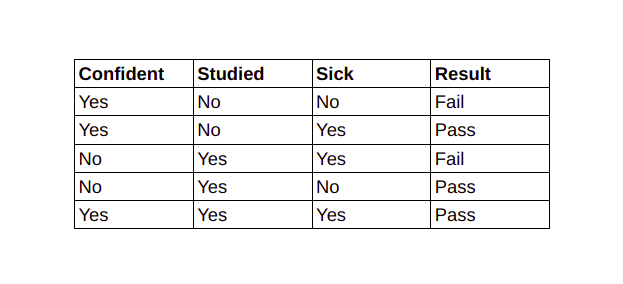
Step by step approach:

1. Consider the above dataset showing the result whether a person is pass or fail in the exam based on various outputs, I have considered a small one for better understanding. And we want to classify an instance 'X' with Confident=Yes, Studied=Yes and Sick=No
2. So, first we need to calculate the class probabilities i.e P(Pass)=3/5 and P(Fail)=2/5
3. Now we need to calculate individual probbaility wit respect to each features. For example,
   P(Confident=Yes| Result=Pass) = 2/3
   P(Studied=Yes| Result=Pass) = 2/3
   P(Sick=Yes| Result=Pass) = 1/3

Similarly,

P(Confident=Yes| Result=Fail) = 1/2
P(Studied=Yes| Result=Fail) = 1/2
P(Sick=Yes| Result=Fail) = 1/2

4. Now we calculate,

P(X|Result=Pass)xP(Result=Pass) = (2/3) * (2/3) * (1/3) * (3/5) = 0.088
P(X|Result=Fail)xP(Result=Fail) = (1/2) * (1/2) * (1/2) * (2/5) = 0.05

5. Next step is to calculate the probability of estimator
   P(X) = P(Confident=Yes)xP(Studied=Yes)xP(Sick=No) = (3/5) * (3/5) * (2/5) = 0.144

6. Finally,
   P(Result=Pass|X) = 0.088/0.144 = 0.611
   P(Result=Fail|X) = 0.05/0.144 = 0.34

As 0.611>0.31, the instnace with 'Confident=Yes, Studied=Yes and Sick=No' has result as 'Pass'.

Now, we will look at the python code for Bernoulli Naive Bayes, where we will craete our own data, train the model, predict the values and test it.

1. Import Libraries

#importing necessary libraries

import numpy as np
from sklearn.naive_bayes import BernoulliNB 
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt

2. Create data

#creating dataset with with 0 and 1

X = np.random.randint(2, size=(500,10))
Y = np.random.randint(2, size=(500, 1))

X_test = X[:50, :10]
y_test = Y[:50, :1]

X will have training data with 500 instances with 10 features each, having values in the form of 0 and 1 only.
The test data contains 50 instances.

First 5 rows of our data looks like:

3. Create and train the model

clf = BernoulliNB()

model = clf.fit(X, Y)

This will create an instance of Bernoulli Naive Bayes model and train it.

4. Predicting an instance

y_pred =clf.predict(X_test)
acc_score = accuracy_score(y_test, y_pred)
print(acc_score)

The model predicts the test instances.
Accuracy of the model is 0.92 i.e 92%

5. Plotting graph

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu')
l = plt.axis()
plt.scatter(Xtest[:, 0], Xtest[:, 1], c=Ytest, s=20, cmap='RdBu', alpha=0.1)
plt.axis(l);

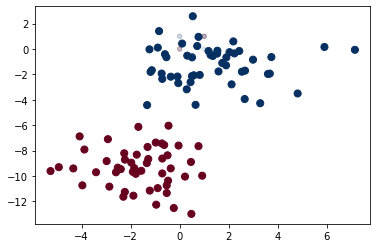
Above is the graph of our model, where red dots represents instances whose value 0 and blue dots represents instances whose value is 1.

Advantages of Bernoulli Naive Bayes:

1. They are extremely fast as compared to other classification models
2. As in Bernoulli Naive Bayes each feature is treated independently with binary values only, it explicitly gives penalty to the model for non-occurrence of any of the features which are necessary for predicting the output y. And the other multinomial variant of Naive Bayes ignores this features instead of penalizing.
3. In case of small amount of data or small documents(for example in text classification), Bernoulli Naive Bayes gives more accurate and precise results as compared to other models.
4. It is fast and are able to make to make real-time predictions
5. It can handle irrelevant features nicely
6. Results are self explanatory

Disdvantages of Bernoulli Naive Bayes:

1. Being a naive(showing a lack of experience) classifier, it sometimes makes a strong assumption based on the shape of data
2. If at times the features are dependent on each other then Naive Bayes assumptions can affect the prediction and accuracy of the model and is sensitive to the given input data
3. If there is a categorial variable which is not present in training dataset, it results in zero frequency problem. This problem can be easily solved by Laplace estimation.

From all the above results we can see Bernoulli Naive Bayes is a very good classifier for problems where the features are binary. It gives very good accuracy and can be esaily trained.

With this article at OpenGenus, you must have the complete idea of Bernoulli Naive Bayes. Enjoy.