Different approaches to calculate Euler's Number (e)

In this article, we have explored different approaches to calculate Euler's Number (e) along with sample implementations to calculate Euler's number to different precision.

TABLE OF CONTENT -

1. INTRODUCTION ABOUT EULER NUMBER
2. APPLICATIONS OF EULER NUMBER (e)
3. CALCULATING METHODS
4. METHOD 1: HORIZONTAL ASYMPTOTE
5. METHOD 2: FACTORIALS

INTRODUCTION -

Euler's number e is among one of the most famous mathematical constants after pi. It has permanent place on our calcultors lets explore about it.
Eulers no. has a value of 2.7182818284590452353602874713527 (and more ...). it is an irrattonal no. and it has decimal expansion which can continue forever without repetition.

Eulers number is used in lot of real life situations and it has many interesting mathematical properties .

Applications of EULER NUMBER (e) -

1. The base rate of growth shared by all continuously growing processes is represented by e.

2. It appears whenever systems grow exponentially and continuously, such as population, interest calculations and radioactive decay.

3. every rate of growth which often do not grow smoothly can be approximated by e (unit growth, perfectly compounded)

4. e represents that all growing processes are scaled version of common rate, when change happens at finite period and find the impact of continuous growth at infinitely smaller intervals

5. e is Important number in mathematics and physics. e.g in calculus slopes and areas ,also in logarithmic calculations, and in physics we use it for representing equations of waves e.g light,sound etc and in many more different fields.

Calculating Euler's Number -

There are many ways of calculating euler's no. but none of them gives accurate answers because e is irrational,
Two most common ways of calculating e are -

1. HORIZONTAL ASYMPTOTE
2. FACTORIALS
   above methods respective equations are shown below-
   

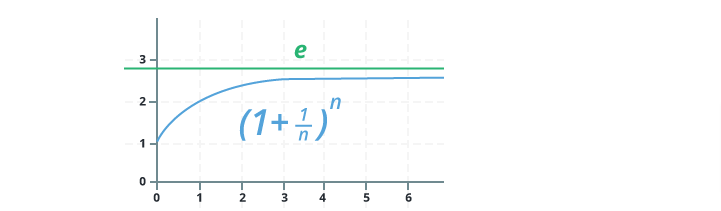
Method 1: Horizontal Asymptote -

e is defined as -

the value of (1 + 1/n)n approaches e as n gets bigger and bigger:

Implementation of above approach in C++-

#include<iostream>
#include<math.h>
using namespace std;
int  main() {
       int Number = 0;
       cout << "Enter Ending Point for Euler Numbers = ";
       cin >> Number;
       for (float i = 1; i <= Number; i++) {
              //(1 + 1 / n)n
              float tempResult = ((1 / i) + 1);
              float result = pow(tempResult, i);
              cout << i << " == " << result << endl;
            
       }
        return 0;
}

output -

Enter Ending Point for Euler Numbers = 20
1 == 2
2 == 2.25
3 == 2.37037
4 == 2.44141
5 == 2.48832
6 == 2.52163
7 == 2.5465
8 == 2.56578
9 == 2.58118
10 == 2.59374
11 == 2.6042
12 == 2.61304
13 == 2.6206
14 == 2.62715
15 == 2.63288
16 == 2.63793
17 == 2.64242
18 == 2.64643
19 == 2.65004
20 == 2.6533

TIME AND SPACE COMPLEXITY-

Time Complexity: O(N)

Auxiliary Space: O(1), since no extra space has been taken.

• where N is the number of digits in e to be calculated.
• High the value of N, closer is e to the real value.

Method 2: Factorials -

In this , we have to calculate the value of Euler’s number using the formula e = 1 + 1 / 1! + 1 / 2!...+1/n!

For that, we have to know about Euler's number. Euler’s number is a sum of infinite series, it is a mathematical constant approximately equal to 2.718. To calculate the value of e, you can use the formula or the expression given below:

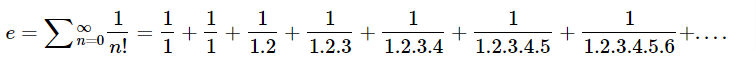
solving above expression we get -

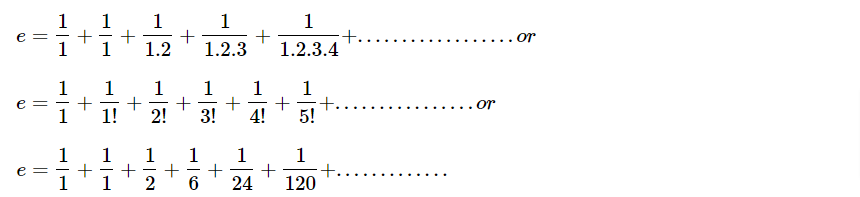
which on siplification gives us -

therefore the exponential constant value e = 2.71828

Implementation of above approach -

#include <iostream>
#include <iomanip>
using namespace std;
int main ()
{
    int i,j;
    double E, D;
    
    for (i=1; i<=15; i++ )
    {
        D=1;
        for (j=1; j<=i ; j++ )
        {
            D = D * j;
        }
        E = E + 1 / D;
    }
    cout<<setprecision(10)<<"Approximate Value of e is "<< E + 1 <<endl;
    }
    

OUTPUT-

Approximate Value of e is 2.718281828

TIME AND SPACE COMPLEXITY-

Time complexity :O(N)
Auxiliary Space : O(1)

• where N is the number of digits in e to be calculated.
• High the value of N, closer is e to the real value.

Time Complexity is O(N) as we are calculating factorial using Dynamic Programming. If we calculate factorial separately for each term, the Time Complexity will become O(N^2).