Table of Contents

1. Word2Vec
2. CBOW
3. Skip-gram
4. Difference
5. Conclusion

This article at OpenGenus gives the idea of CBOW (Continuous Bag of Words) and Skip-gram in a detailed way along with differences between the two concepts.

Word2Vec

Mechine Learning (ML) algorithms can not work with the words as we human can, but they can work with numbers. For this reason, every word present in the given document or context is encoded into a vector. This encoding is called one hot encoding. Let's talk about what's one hot encoding is.

One hot encoding

A document or context is given. There are N number of total words (vocabulary) and K number of unique words. For each of these K unique words, a vector of size N is generated. In this vector, the position in the document/context where the word is found, is assign as 1. Otherwise 0 is assigned for that position. Let's look at the following example for better understanding:

Suppose,
 Our document/context hold the following sentence:

The horror, the horror that has come after the announcement is made.

Here,
 Number of total words, N = 12
 Number of unique words, K= 9
 One hot encoding for each of the unique words will be as following:

words	the	horror	the	horror	that	has	come	after	the	announcement	is	made
the	1	0	1	0	0	0	0	0	1	0	0	0
horror	0	1	0	1	0	0	0	0	0	0	0	0
that	0	0	0	0	1	0	0	0	0	0	0	0
has	0	0	0	0	0	1	0	0	0	0	0	0
come	0	0	0	0	0	0	1	0	0	0	0	0
after	0	0	0	0	0	0	0	1	0	0	0	0
announcement	0	0	0	0	0	0	0	0	0	1	0	0
is	0	0	0	0	0	0	0	0	0	0	1	0
made	0	0	0	0	0	0	0	0	0	0	0	1

Most of the entries in this type of table is 0. This type of table is called sparse table.

CBOW(Continuous Bag of Words)

In CBOW, the context is given but keyword/s (target word/s) will be missing from the context, which the Neural Network(NN) model will predict. For example the given context will be like the following one:

The horror, the horror that has ____ after the announcement is made.

Window Size

Window Size indicates the number of the words given as input into NN. If the window size is 2, then two words before the target word and two words after the target words will be given as input.

For the example above,

The horror, the horror that has ____ after the announcement is made.

Suppose the target word has the position C, then the positons and the words to be predicted will be:

C-2	C-1	C	C+1	C+2
that	has	____	after	the

If has a window size of m, then the words from C-m to C+m positions except C position (target word), will be taken as input. It can be seen, for a window size of m, the number of the selected words will be 2*m. Here, as the window size is 2, the number of the words will be selected, 2*2 = 4.

After this, each of the words will be encoded (following the concept shown above). In this case, 4 words will be encoded as it has been shown below:

words	the	horror	the	horror	that	has	come	after	the	announcement	is	made
that	0	0	0	0	1	0	0	0	0	0	0	0
has	0	0	0	0	0	1	0	0	0	0	0	0
after	0	0	0	0	0	0	0	1	0	0	0	0
the	0	0	0	0	0	0	0	0	1	0	0	0

And they will be integrated into one vector named Input vector:

words	the	horror	the	horror	that	has	come	after	the	announcement	is	made
Input	0	0	0	0	1	1	0	1	1	0	0	0

This Input is the input vector that will be given as an input to the NN which will have rows equal to the size of the vocabulary, N. In general it will have a size of N×1 (N rows and 1 column). In this case N = 12 (total number of words). So, the Input Vector will have a size of 12×1. The Input Vector will look like the following:

Input
0
0
0
0
1
1
0
1
1
0
0
0

Now, the probability (P) of the words, given in the context, will be predicted which can be at the position C given the words from positions C-m to C+m except C.

P(word | (word at C-m, word at C-(m+1), ... , word at C-1, word at C+1, ... , word at C+m))

In our case:

P(word | (word at C-2, word at C-1, word at C+1, word at C+2))
or,
P(word | that, has, after, the)

Here the word will be any word given in the context, In our case it will be any word from the following context mentioned earlier:

The horror, the horror that has come after the announcement is made.

Here the order of the context words which have been given don't matter. The target word is predicted based on the given set of words. The model predicts the probability (probability of being the target word) for any word as a continuous value rather than an integer value. And a word is picked from a bag of words, that's why it is called Continuous Bag Of Words.

Architecture of the Neural Network

The neural network has two layers:

1. Hidden Layer
2. Softmax Classifier

Hidden Layer:

There can be k neurons (also called dimensions) in this layers. k can be any number, but it's usually 0 < k < N. For our case, suppose we have 4 neurons. For each of these k = 4 neurons there will be N = 12 features, which will create a matrix of M1 = k×N = 4×12 matrix.

In our case only 4 values of the input vector are 1 and others are 0. So, in probability calculation only those 4 values with the value of 1 will keep an effect. And for others with the value of 0, the probability will become 0.

For every of the 4 values, we will take their encoded value vector of size N = 12×1 (like the input vector) and multiply it with M1 = k×N = 4×12.

Equation:
$V_i = M1*V_i(encode)$

Encoded Values:

words	the	horror	the	horror	that	has	come	after	the	announcement	is	made
that	0	0	0	0	1	0	0	0	0	0	0	0
has	0	0	0	0	0	1	0	0	0	0	0	0
after	0	0	0	0	0	0	0	1	0	0	0	0
the	0	0	0	0	0	0	0	0	1	0	0	0

After the multiplication, for each of them we will get a vector of size M1*N = k×1 = 4×1. Suppose for the words that, has, after and the, these vectors are V1, V2, V3, and V4 repectively. We will calculate a vector of V from these four vectors using the equation below:

\begin{align}
V &= \frac{V1 + V2 + V3 + V4}{ 2*m}
\end{align}

V will also have a size of 4×1.

Softmax Classifier:

For this layer another matrix, M2 will be created. It will have a size of N×k = 12×4 and it will lead to the output.

Now if the M2 * V are multiplied, then the output vector of size M2 * V = N×1 = 12×1 will be generated, this output vector has the size of the input vector.

From this vector, the word with the highest probability will be chosen as the target word.

Graphical view of CBOW architecture:

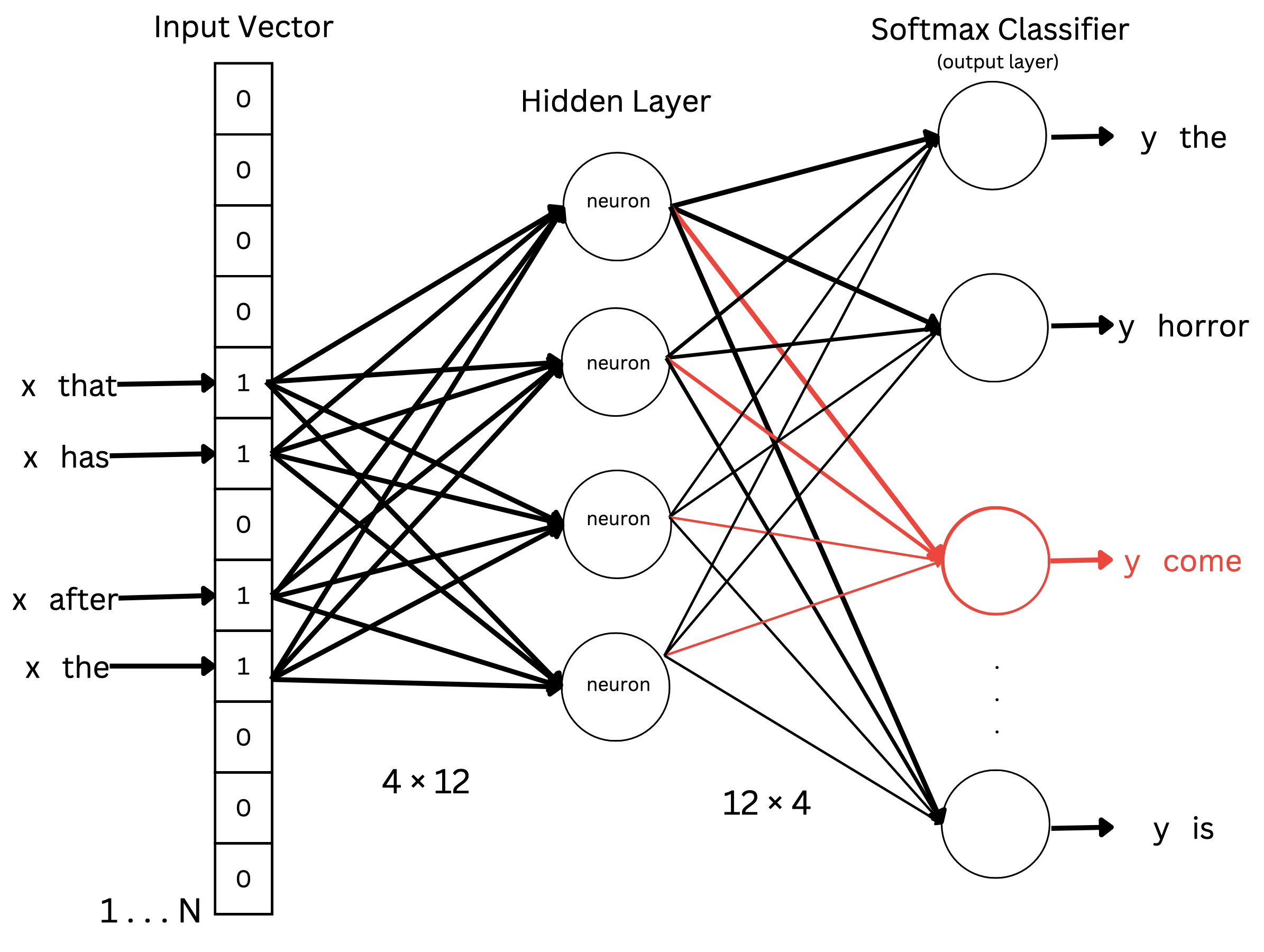
Let's say the 4 inputs are x and the output is the y.

The probability will be calculated as though the right word come has the highest probability in the output vector.

For every word in the given document/context the measured P is noted down in output vector. P is calculated using the probability function that has been mentioned above. And the word which has the highest probability is selected. Every word of the given context will be considered as a probable candidate for y, but ultimately the word which has the highest probability will be selected as the value of y.

Skip-gram

Skip-gram works pretty much the same way as the CBOW does. The difference in skip-gram is that it takes the target word as input and returns the context words as output, otherwise reverse of CBOW.

Window

Like CBOW, the window of size m indicates to the words from C-m to C+m except C which is the position of the target word. If the window size is 2, then words from position C-2 to position C+2 have to be predicted, assuming the word in position C is given. Let's look at an example for skip-gram:

The horror, the horror ____ ___ come _____ ___ announcement is made.

Given the target word come, two words which are before come and two words which are after come have to be predicted. Here, given a window size of m, 2*m words have to be predicted by the model.

For predicting the words the model will calculate the probability of a set of tuples consisting of two words. The first element of the tuples will change, it will iterate over the document/context and take each word as it element for one tuple. For the second element, it will always remain the the same, it will be the target word. For the given context (mentioned above):

The horror, the horror that has come after the announcement is made.

Ultimately probability of the following tuples will be the highest ones in the output vector as they are the closest context words to come:

(that, come)
(has, come)
(after, come)
(the, come)

Remember one thing, even though the position of the context word doesn't matter in the CBOW, it matters in case of skip-gram. As the multiple close context words will be selected here, which are the most closest context words for the target words and they will also have the highest probability values in the ouput vector.

Architecture

The architecture remains the same as CBOW. The input will be changed, it will take the encoded vector of the target word as input. For our case it will be as following:

Input
0
0
0
0
0
0
1
0
0
0
0
0

The M1 and M2 matrix will be calculated in the same fashion. Only the last input will be changed. It will predict multiple tuples based on the predicted probability values. it will choose the 2*m (m is the window size) tuples that have the highest probability values. And among these tuples, the the order of the tuples from the target word will be determine with the increasement or decreasement of their probability values. A tuple with higher probability value is closer to the target word than a tuple which has the lower probability value than the first one.

The probability function will for Skip-gram is:

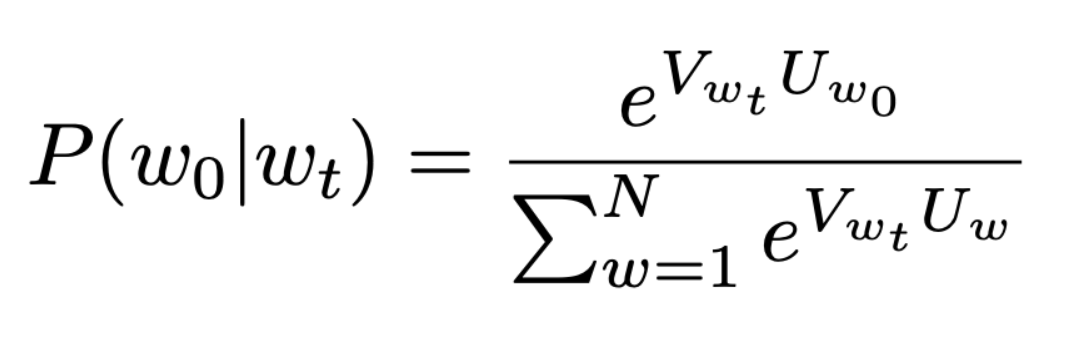
Here, w₀ is any specific word from the context for which measuring the probability is being measured and w_t is the target word. V and U_w0, U_w are the vectors of the target word, specific word and other words respectively.

Difference

Here are the differences between the two concepts:

CBOW	Skip-gram
CBOW is used when there is a need to predict the target word or center word given that context words are known	Skip-gram is used when there is a need to predict the context words that only the target word is known
In CBOW the context words are given as input	In Skip-gram only the target word is given as input
In CBOW the model gives the target word as output	In Skip-gram the model gives the context words as output
CBOW trains several times faster than Skip-Gram	Skip-gram trains several times slower than CBOW
CBOW gives slightly better accuracy for more frequent words	Skip-gram better represents less frequent words or phrases
CBOW works well with larger datasets	Skip-gram works well with smaller datasets

Conclusion

Even though we have tried to discuss CBOW and Skip-gram in details in this article, we have not discuss about dimension as this needs a whole article to discuss fairly. Also for the simplicity of the learning, it has been shown that the hidden layer is consisted of 1 layer only. In reality, this layer is consisted of multiple layers underneath. There also may have some other missed information or errors due to human nature. Lastly, the following picture is the perfect one to conclude this article.

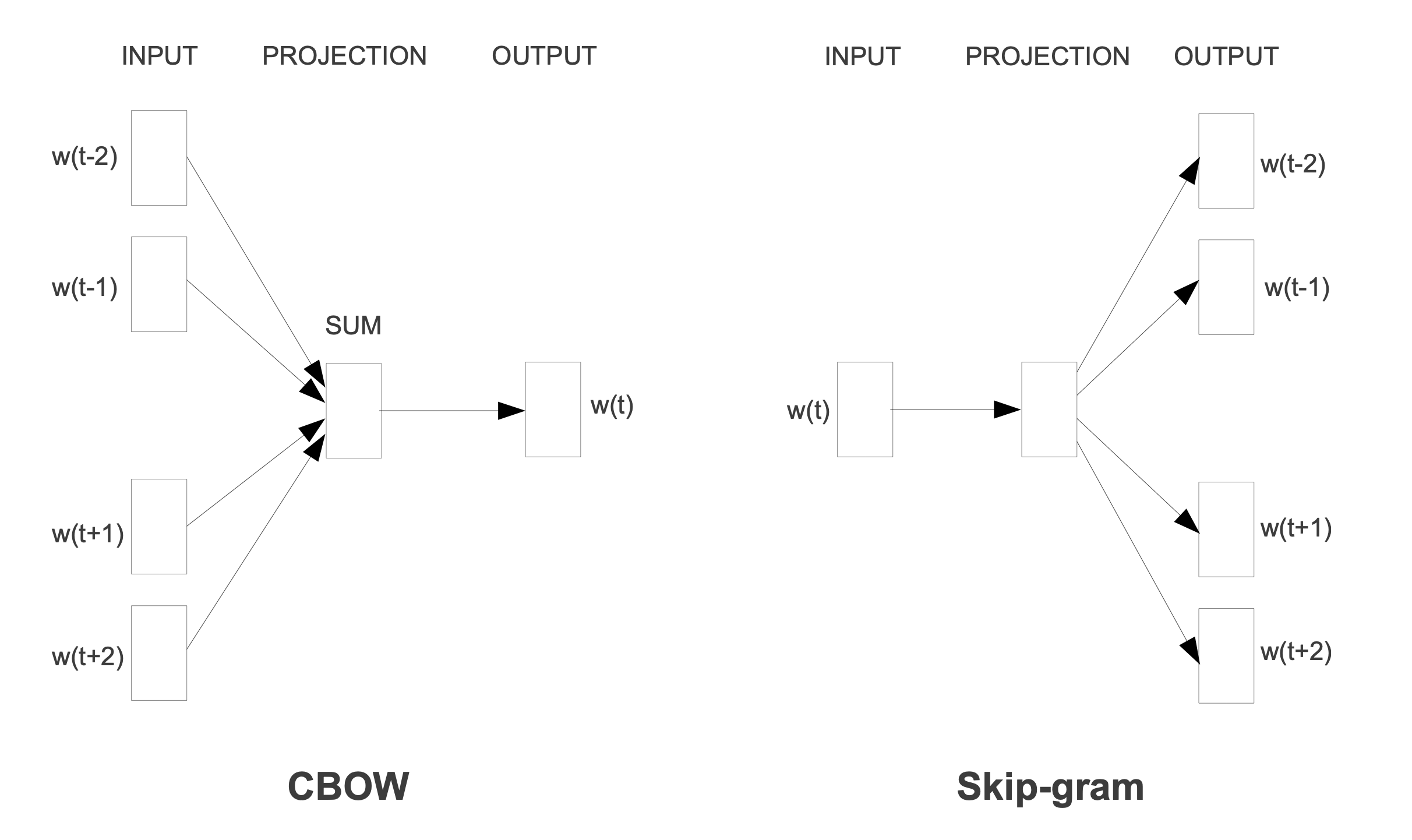
Source: Exploiting Similarities among Languages for Machine Translation paper