
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will discuss how we can convert a binary number to a hexadecimal, octal, and decimal number.
Table of contents:
- How to convert from Binary to Hexadecimal
- How to convert from Binary to Octal
- How to convert from Binary to Decimal
Let us get started with discussing how different types of numerical systems such as hexadecmial, octal, and decimal can be obtained from a binary number through conversion.
How to convert from Binary to Hexadecimal?
Step 1: Seperate your binary number into groups of 4.
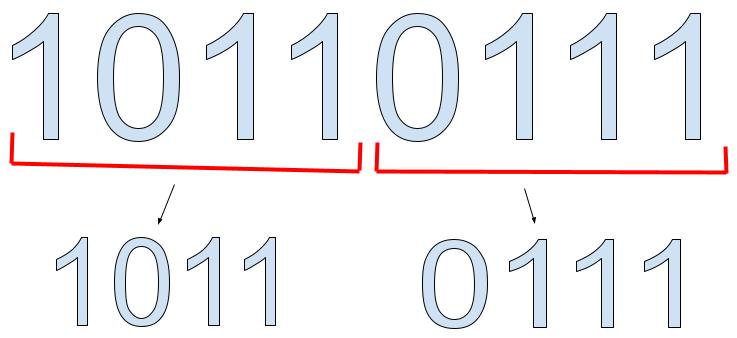
Step 2: Now we have to convert the binary numbers to decimal values.
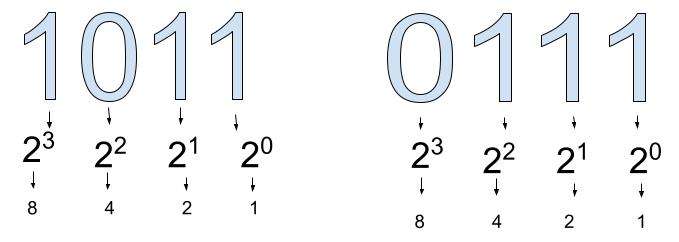
Step 3: Multiply the decimal values by their binary number and add them all up.
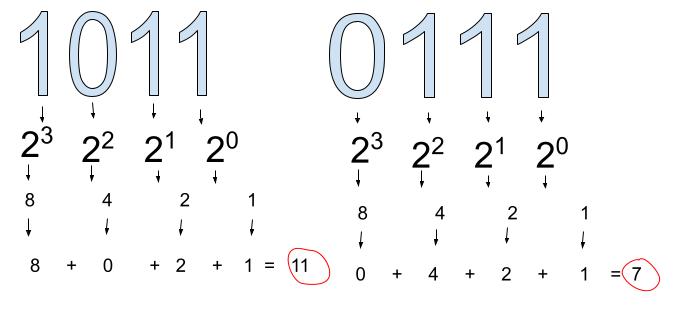
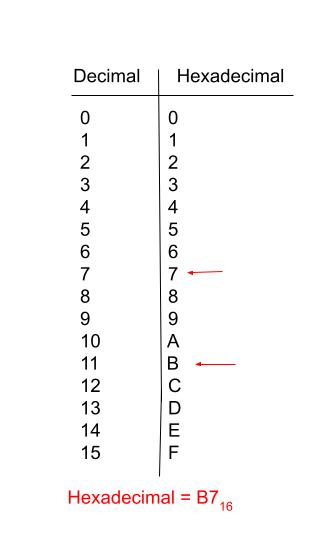
Step 4: Now we can convert the numbers we have obtained to hexadecimal values using the following hexadecimal chart. From the chart we can see that the number 7 corresponds to "7" on the chart while the number 11 corresponds to "B". Since hexadecimals are a base 16 system. We put 16 after B7 using subscript.
Now let us discuss how we can create a program consisting of pseudocode and implementation on how to convert binary to hexidecimal.
# Convert from Binary to decimal and then convert from decimal to hexadecimal (process)
# Create an list called hexa that is blank.
hexa = []
# Create a variable called result that will print the reversed hexadecimal.
result = []
# create a variable called num that will be the number input from the user.
num = int(input("Enter any number: "))
# Create a variable called des to determine the sum of the decimal value.
des = 0
# Create a variable called i that will be the index of the list.
i = 0
# Create a variable called temp to copy the num variable value.
temp = num
# Create a while loop that will run as long as the temp variable is greater than 0.
while temp > 0:
# Create a variable called rem that will be the remainder of the temp % 10
rem = int(temp % 10)
# Create a variable called des that will be the sum of the des variable and the rem variable.
des = des + rem * pow(2, i)
# Increment i by 1 each time the loop runs. This will be the index of the list. To move on to the next element in the list.
i = i + 1
# Divide the temp variable by 10 to get the next digit. That will go through the loop again.
temp = int(temp / 10)
# Now we have convert our number to decimal. We can print it to confirm. We can felete this after.
print("Decimal: ", des)
# Set i = 0` to start the loop again and interate through the decimal value.
i = 0
# Create a variable called rem that will be the remainder.
rem = 0
# Create a while loop that will run as long as the des variable is greater than 0.
while des > 0:
# Since hexadecimal is base 16, we can use the des % 16 to get the remainder.
rem = int(des % 16)
# Check if the remainder is between 0 and 9 or between 10 and 15.
if rem < 10:
# If the remainder is between 0 and 9, we can add the remainder to the list.
hexa.append(chr(rem + 48))
else:
# If the remainder is between 10 and 15, we can add the remainder to the list.
hexa.append(chr(rem + 55))
# Then we can decrement the divide des variable by 16 to get the next remainder.
des = int(des / 16)
# Start the loop again to reverse the list. This is 1.
j = 1
# For loop to interate through the list. Starting from i.
for i in hexa:
# Append the reversed list to the result variable.
result.append(hexa[len(hexa) - j])
# Now we can increment j by 1 each time the loop runs.
j = j + 1
# Print the reversed hexadecimal.
print(result)
Time Complexity = O(N), dependent on user input size.
How to convert from Binary to Octal?
Step 1: separate binary number into groups of 3.
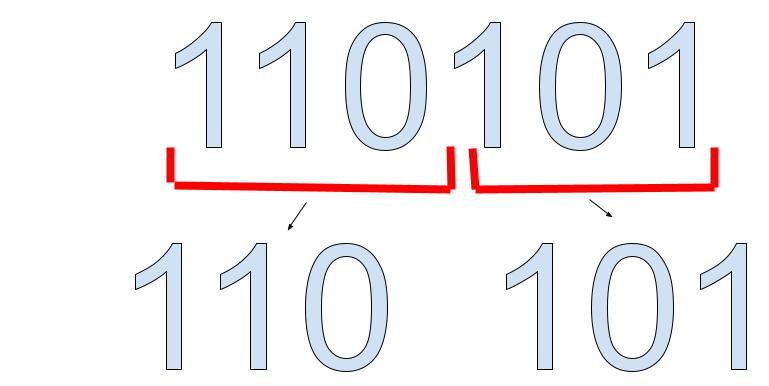
Step 2: Multiply each digit in the group of 3 by the numbers under them.
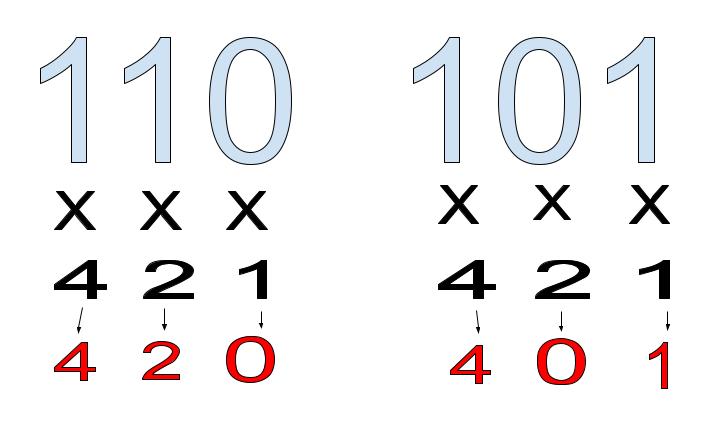
Step 3: Add the numbers in the two groups up and combine them. Put an 8 after the number in subscript to make it in the base 8 system which is octal.
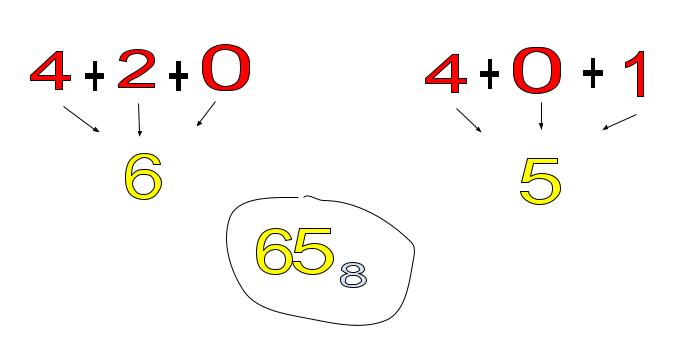
Now let us discuss how we can create a program consisting of pseudocode and implementation on how to convert binary to octal.
# Create a list with a binary number and store it in num variable.
num = [110101]
# Create a variable called oct_num and set its value to 0.
oct_num = 0
# Create a variable called dec_num and set its value to 0.
dec_num = 0
# Create a variable called a and set its value to 0.
a = 0
# Loop until the input binary number is not equal to zero using a while loop.
print(f"The Octal value binary number {num} is: ")
while (num != 0):
# Inside the loop, get last digit using modulus operator and use value of 10
# Create a variable called b and store it in the value of the modulus operator.
b = (num % 10)
# Get the value of 2 raised to the power of a using the pow() function and multiply
# it with the value b from above.
# Store it in a variable called c
c = pow(2, a) * b
# Add c value to the dec_num variable and store it in the same variable dec_num.
dec_num = dec_num + c
# Increase the value a by 1 and store in variable a.
a += 1
# Divide the given binary number by 10 and store it in the variable num.
num = num // 10
# exit while loop and set the value of variable with 1.
a = 1
# Loop until the decimal number is not equal to zero from a while loop.
while (dec_num != 0):
# Multiply variable a value with the num modulus 8 and store it in a variable called d. This will give the octal value.
d = (dec_num % 8) * a
# Add the value of d with the oct_num variable and store it in that variable.
# variable oct_num.
oct_num = oct_num + d
# Divide the dec_num by 8 and store it in dec_num variable.
dec_num = dec_num // 8
# Multiply a with 10 and store it iun a variable called a.
a = a * 10
# Print the oct_num to finish program. .
print(oct_num)
Time Complexity = O(N), dependent on user input size.
How to convert from Binary to decimal?
Step 1: Multiply each digit in the binary number by its corresponding powers of two.
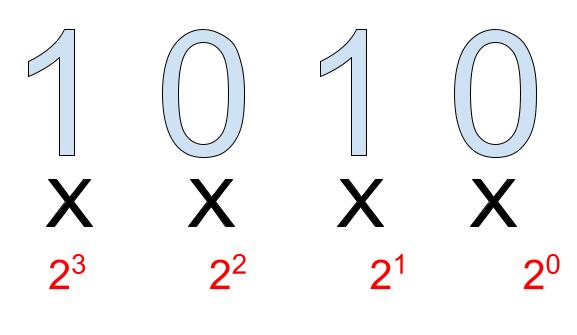
Step 2: Add all of the values to calculate your decimal number.
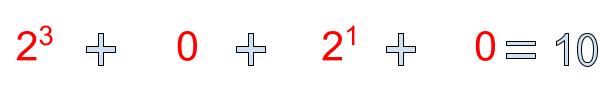
Now let us discuss how we can create a program consisting of pseudocode and implementation on how to convert binary to decimal.
# Convert from Binary to decimal
# Create an list called hexa that is blank.
hexa = []
# Create a variable called result that will print the reversed hexadecimal.
result = []
# create a variable called num that will be the number input from the user.
num = int(input("Enter any number: "))
# Create a variable called des to determine the sum of the decimal value.
des = 0
# Create a variable called i that will be the index of the list.
i = 0
# Create a variable called temp to copy the num variable value.
temp = num
# Create a while loop that will run as long as the temp variable is greater than 0.
while temp > 0:
# Create a variable called rem that will be the remainder of the temp % 10
rem = int(temp % 10)
# Create a variable called des that will be the sum of the des variable and the rem variable.
des = des + rem * pow(2, i)
# Increment i by 1 each time the loop runs. This will be the index of the list. To move on to the next element in the list.
i = i + 1
# Divide the temp variable by 10 to get the next digit. That will go through the loop again.
temp = int(temp / 10)
# Now we have convert our number to decimal. We can print it to confirm. We can felete this after.
print("Decimal: ", des)
Time Complexity = O(N), dependent on user input size.
Real life applications
- While computer networks and devices use binary-based addressing, humans utilize decimal-based addressing. We can receive information in a language that is simple for us to understand thanks to conversions.
