
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
This is the most complete Data Science Cheatsheet which you should follow to revise all Data Science concepts within 30 minutes and get ready for Interviews and stay in form.

| Data science lifecycle | ||
|---|---|---|
| Phase | Description | |
| Discovery | ||
| Understanding data | Involves describing what data is needed, how relevant are they and finally extracting the required data. | |
| Data preparation | ||
| Data analysis | ||
| Model planning | Decide on our machine learning model based on the business problem. | |
| Model building and deployment | Create and evaluate the ML model and finally deploy it in the preferred environment. | |
| Communication of results | ||
| Machine Learning | ||
|---|---|---|
| Supervised Learning | Type of machine learning technique where models are trained using labeled data as inputs. Commonly used fore regression and classification tasks. | |
| Unsupervised Learning | Type of machine learning technique where models are trained using unalbeled data as inputs. Used for extracting information from large amounts of data. | |
| Semi-supervised Learning | Combination of supervised and unsupervised learning where a small amount of inputs are labeled and large portions of them are unlabeled. | |
| Reinforcement Learning | This is a machine learning technique concerned with teaching agents to take decisions in environment to maximize the reward. | |
| Regression | ||
| Classification | These algorithms are used to categorize the given test data accurately, such as telling apart a cat from a dog. | |
| Ensemble Learning | Ensemble methods helps improve the performance of a machine learning model by combining several ML base models to produce one single predictive model. | |
| Recommender Systems | ||
| Supervised Learning | |||
|---|---|---|---|
| Algorithm | Description | Advantages | Disadvantages |
| Logistic Regression | An algorithm that models linear relationship between inputs and outputs a categorical variable. | ||
| Linear Regression | An algorithm that models linear relationship between inputs and produces continuous outputs. | ||
| Support Vector Machines | An algorithm that aims to create the best decision boundary to group n-dimensional space into different classes. | ||
| Random Forest | It is a combination of many decision trees and is an ensemble learning method. | ||
| Decision Tree | An algorithm that can be used for both regression and classification where models make decision rules on features to obtain predictions. | ||
| K-Nearest Neighbors | An algorithm that uses feature similarity to predict values of new data points. | ||
| Unsupervised Learning | |||
|---|---|---|---|
| Algorithm | Description | Advantages | Disadvantages |
| K-Means Clustering | A clustering algorithm that determines K clusters based on euclidean distances. | ||
| Hierarchical Clustering | |||
| DBSCAN | |||
| Apriori Algorithm | |||
| Principal Component Analysis | This algorithm is widely used for dimensionality reduction. | ||
| Manifold Learning | It is used for non-linear dimensionality reduction and aims to describe datasets as low-dimensional manifolds embedded in high-dimensional spaces. | ||
| Deep Learning | ||
|---|---|---|
| Neural Network | A neural network takes an input, passes it through multiple layers of hidden neurons and outputs a prediction representing the combined input of all the neurons. | |
| Architectures |
| |
| LSTM | LSTM is a variant of RNN that is used for learning long term dependencies. It has a memory cell to record additional information. | |
| Back propagation | A back propagation algorithm consists of two main steps:
| |
| Gradient descent | ||
| Activation function | ||
| Loss function | ||
| Optimizers | | |
| Regularization | It is a technique for combating overfitting and improving training. Some of them are early stopping, data augmentation and ensembling. | |
| Layers |
| |
| Python Basics | ||
|---|---|---|
| Concept | Code | Description |
| NumPy | ||
| Creating arrays | ||
| Inspecting the array | ||
| Arithmetic Operations | ||
| Aggregate functions | ||
| Subsetting and Slicing | ||
| Array manipulation | ||
| Pandas | ||
| Series | s = pd.Series([3, -5, 7, 4], index=['a', 'b', 'c', 'd']) | A one-dimensional labeled array a capable of holding any data type |
| DataFrame | data = {'Country': ['Belgium', 'India', 'Brazil'],
'Capital': ['Brussels', 'New Delhi', 'Brasília'],
'Population': [11190846, 1303171035, 207847528]} df = pd.DataFrame(data, columns=['Country', 'Capital', 'Population']) | A two-dimensional labeled data structure with columns of potentially different types |
| Reading csv files | pd.read_csv('file.csv', header=None, nrows=5) | |
| Selecting and setting | ||
| Sorting and dropping | ||
| Retrieving basic dataframe information | ||
| Summary of dataframe information | ||
| Statistics and Probability | ||
|---|---|---|
| Concept | Description | Formula/Graph |
| Mean | The mean denotes the average of the group of finite numbers. | 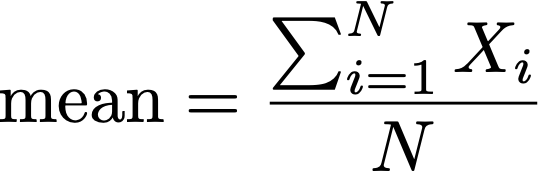 |
| Median | The median denotes the middle of an ordered set of data. | 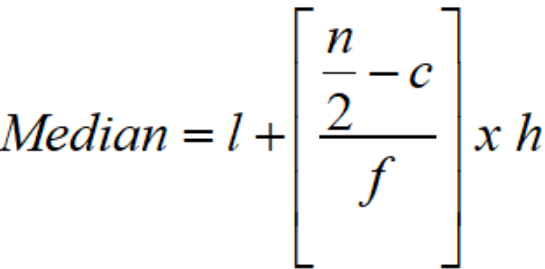 |
| Mode | Is only relevant for discrete data and is the the most common value occurring in a dataset. | 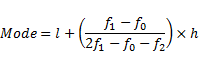 |
| Variance | Variance gives a measure of the degree to which each value in the population/sample differs from the mean value. | 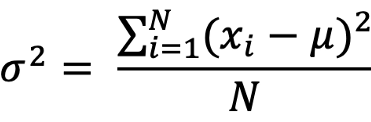 |
| Standard deviation | The standard deviation tells us how much the values in the sample/ population is spread out from the mean value. | 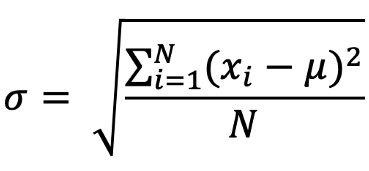 |
| Covariance | Covariance is used to identify how they both change together and also the relationship between them. | 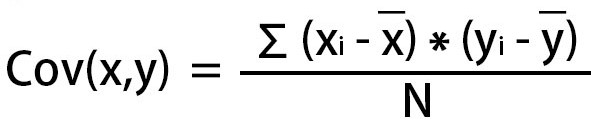 |
| Correlation | Correlation is dimensionless and is used to quantify the relationship between two variables. It has its range as [-1,1]. | 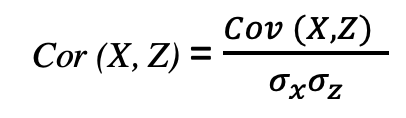 |
| Central limit theorem | It states that "As the sample size becomes larger, the distribution of sample means approximates to a normal distribution curve." | |
| Law of large numbers | The law of large numbers states that As the number of trials or observations increases, the actual or observed average approaches the theoretical or expected average. | |
| Bayes theorem | 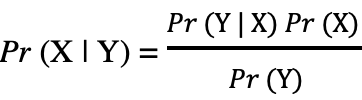 | |
| Hypothesis testing | ||
| A/B testing | A/B testing is a famous testing technique used to compare two variants to determine the best of the two based on user experience. | |
| Confidence intervals | A Confidence interval expresses a range of values within which we are pretty sure that the population parameter lies | 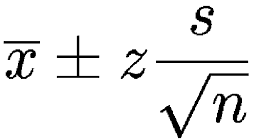 |
| Normal distribution | 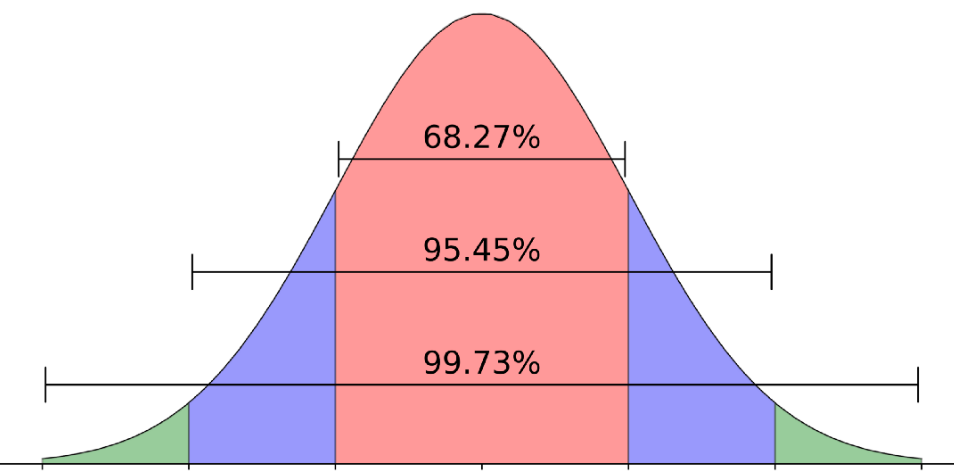 | |
| Poisson distribution | Distribution that expresses the probability of a given number of events occurring within a fixed time period | 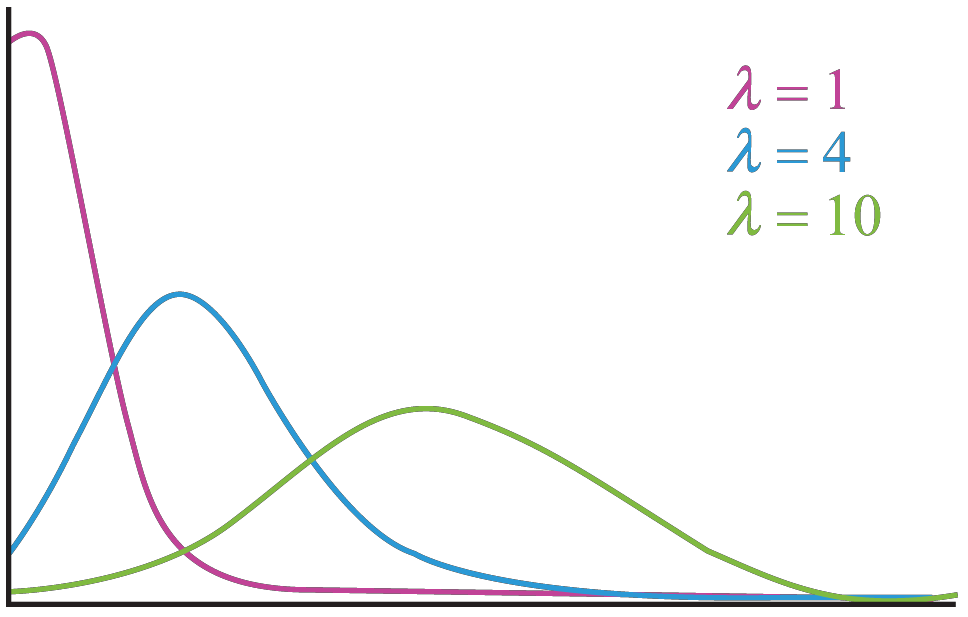 |
| Data visualization | ||
|---|---|---|
| Chart | Description | Image |
| Capturing trends | ||
| Line chart |  | |
| Area chart |  | |
| Capturing distributions | ||
| Histogram |  | |
| Boxplot | Shows the distribution of a variable using 5 key summary statistics. |  |
| Violinplot |  | |
| Part to-whole charts | ||
| Pie chart |  | |
| Donut chart |  | |
| Heatmap |  | |
| Stacked chart | Compare subcategories within categorical data. |  |
| Visualising relationships | ||
| Bar/column chart |  | |
| Scatter plot |  | |
| Bubble chart |  | |
| Time series analysis | ||
|---|---|---|
| Concept | Description | Code |
| ACF plot | The autocorrelation function (ACF) plot shows the autocorrelation coefficients as a function of the lag. | import statsmodels.api as sm sm.graphics.tsa.plot_acf(data) |
| PACF plot | The partial autocorrelation function (PACF) plot shows the partial autocorrelation coefficients as a function of the lag. | import statsmodels.api as sm sm.graphics.tsa.plot_pacf(data) |
| ADF test | If a series is stationary, its mean, variance, and autocorrelation are constant over time. We can test for stationarity with augmented Dickey-Fuller (ADF) test. | from statsmodels.tsa.stattools import adfuller p_value= adfuller(data) |
| Time series decomposition | Separate the series into 3 components: trend,seasonality, and residuals | from statsmodels.tsa.seasonal import STL decomp=STL(data,period=m).fit() plt.plot(decomp.observed) plt.plot(decomp.trend) plt.plot(decomp.seasonal) plt.plot(decomp.resid) |
| Moving average model – MA(q) | The moving average model: the current value depends on the mean of the series, the current error term, and past error terms. | from statsmodels.tsa.statespace.sarimax import SARIMAX model=SARIMAX(data,order=(0,0,q)) |
| Autoregressive model – AR(p) | The autoregressive model is a regression against itself. This means that the present value depends on past values.
| from statsmodels.tsa.statespace.sarimax import SARIMAX model=SARIMAX(data,order=(p,0,0)) |
| ARMA(p,q) | The autoregressive moving average model (ARMA) is the combination of the autoregressive model AR(p), and the moving average model MA(q). | from statsmodels.tsa.statespace.sarimax import SARIMAX model=SARIMAX(data,order=(p,0,q)) |
| ARIMA(p,d,q) | The autoregressive integrated moving average (ARIMA) model is the combination of the autoregressive model AR(p), and the moving average model MA(q), but in terms of the differenced series. | from statsmodels.tsa.statespace.sarimax import SARIMAX model=SARIMAX(data,order=(p,d,q)) |
| SARIMA(p,d,q)(P,D,Q)m | The seasonal autoregressive integrated moving average (SARIMA) model includes a seasonal component on top of the ARIMA model. | from statsmodels.tsa.statespace.sarimax import SARIMAX model=SARIMAX(data,order=(p,d,q),seasonal_order=(P,D,Q,m)) |
