Detect a loop in a linked list (3 methods)

A linked list a liner data structure. A linked list can be of many type. Some popular linked lists are given below:

• Single Linked List
• Double Linked List
• Circular Linked List
• Double Circular Linked List
• Header Linked List

A Loop in a linked list is a condition when a Linked list does not have any end. That means the last pointer does not point to null in case of single and double linked list and to the head of the linked list in case of circluar linked list insted it points to some other node in the linked list.A loop is also known as cycle in a linked list.

We will detect the cycle in single linked list by different methods in this article.

A Single linked list having loop can be seen as the diagram below:

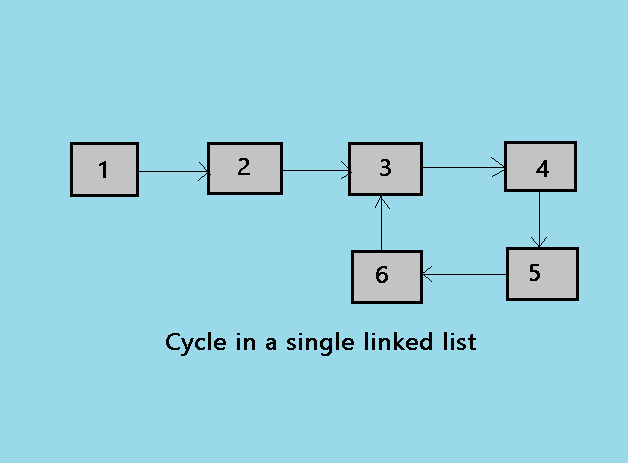
Here are some methods to detect the loops in a Linked List.

• By marking visited nodes
• Using HashMap
• Floyd's cycle finding algorithm

Below is the detailed description of these methods:

Marking Visited Nodes

For using this method we have to modify the linked list data structure. now the class node will contain one more data field in this article we have taken that filed as marked.

• Have a marked with each node.
• As linked list is traversed mark the marked for each node.
• If you mark a visited node again then there is a loop.

pseudocode for the method

The pseudocode of the above method is given below:

• create linked list with one additional data field.
• initialize this data filed with 0 while adding the node in the linked list.
• visit the nodes of the linked list if one node is visited more than once there is a loop.
• if a node is visited more than once then there is a loop in the linked list.

Implementation of Marking visited nodes

#include <bits/stdc++.h> 
using namespace std; 
class node
{
   public:
    int data;
    int marked;
    node* next;	
};
node* head=NULL;
class Linkedlist
{
public:
    void insertnode(int value)
{
    node* new_node=new node();
    new_node->data=value;
    new_node->marked=0;
    if(head==NULL)
    head=new_node;

    else
    {
        new_node->next=head;
        head=new_node;
    }
}

void createloop()
{
    node* temp=head;
    while(temp->next!=NULL)
    {
        temp=temp->next;
    }
    temp->next=head;
}
int detectloop()
{

    while(head->next!=NULL)
    {

        head->marked=head->marked+1;
        head=head->next;
        if(head->marked>1)
        {
            cout<<"loop"<<endl;
            return 1;
        }

    }

    return 0;

}
};
int main()
{
Linkedlist obj;
int a;
//insert nodes in linkedlist
obj.insertnode(3);
obj.insertnode(9);
obj.insertnode(7);
obj.insertnode(4);
obj.insertnode(5);
//create loop for testing
obj.createloop(); 
// detect loop
a=obj.detectloop(); 
head=NULL;
obj.insertnode(6);
obj.insertnode(7);
obj.insertnode(9);
obj.insertnode(10);
obj.insertnode(11);
a=obj.detectloop();

if(!a)
cout<<"no loop"<<endl;

}

Output:

loop
no loop

Example of the the method

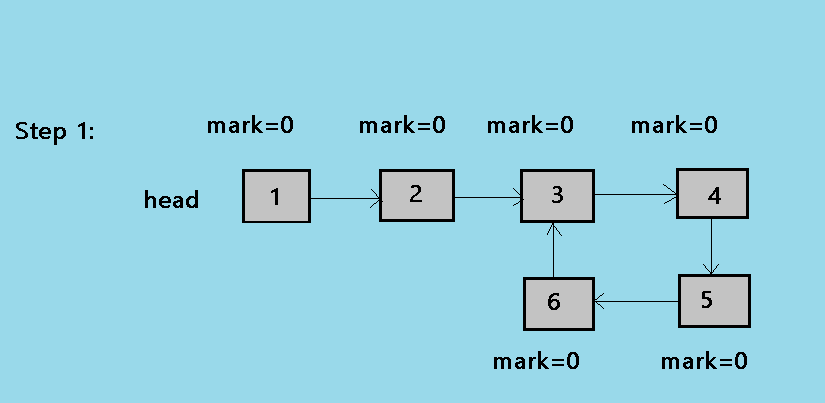
1.As shown in the above picture,Initially all the nodes are marked as 0.

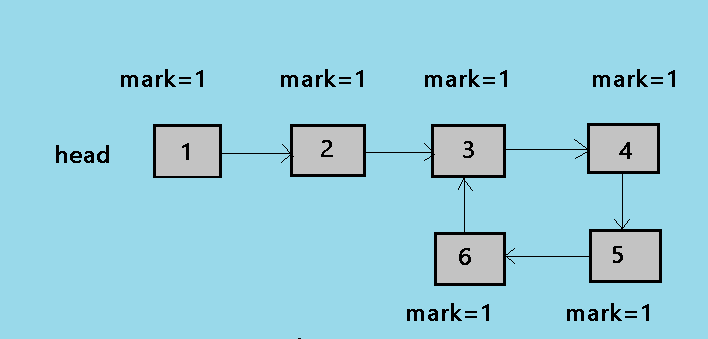
2.Now we traverse the linked list and mark each node as 1.

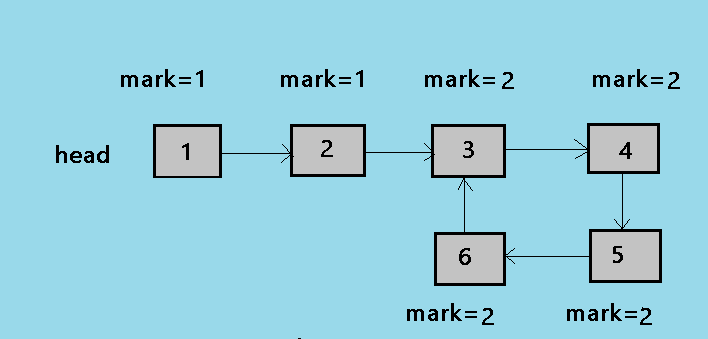
3.After the next step all the nodes in the loop are marked as 2.Now when the node 3 is traversed again it is already marked as 2 it shows that there is a cycle and the while loop is terminated by a break.

Explanation for detect loop

Each node contains one flag(marked) with it for which we have to modify the linked list data structure a bit.Each node initially has it's marked as 0.when we traverse the linked list we mark the marked as 1. So each node has it's marked 1. If there is a Loop in the linked list in that case the marked becomes 2 for that node and the function returns true.
else the loop terminates and function returns false.

• Time complexity: Big O(n)
• Space complexity: Big O(n)

Using HashMap

In this approach as we traverse the list we put the address of each node into the hash table.If there is a loop in the linked list then at some point the next of the current node will point to the previously stored node in the linked list. If there is no loop then when the whole list is traversed and the NULL is reached false will be returned else true will be returned.
Note: for using this approach you should be having some understanding of STL.

pseudocode for the method

pseudocode for the above methos is below:

• Visit each node of the linked list one by one and put the each node addresses in a Hash Table.
• At any point, if NULL is reached then return false and if next of current node points to any of the previously stored nodes in Hash then return true.

Implementation of Hashing method

#include <bits/stdc++.h> 
using namespace std; 
class node
{
   public:
    int data;
    node* next;	
};
node* head=NULL;
class Linkedlist
{
public:
    void insertnode(int value)
{
    node* new_node=new node();
    new_node->data=value;

    if(head==NULL)
    head=new_node;

    else
    {
        new_node->next=head;
        head=new_node;
    }
}

void createloop()
{
    node* temp=head;
    while(temp->next!=NULL)
    {
        temp=temp->next;
    }
    temp->next=head;
}
bool detectloop()
{
    set<node*> s; 
    while (head != NULL) { 
    //if node is alreay in the hash
    //then there is a loop hence return 
    //true
    if (s.find(head) != s.end()) 
        return true; 

    //insert the node into hash if it
    //is traversed for the first time
    s.insert(head); 

    head = head->next; 
} 

return false; 


}
};
int main()
{
Linkedlist obj;
//insert nodes in linkedlist
obj.insertnode(3);
obj.insertnode(9);
obj.insertnode(7);
obj.insertnode(4);
obj.insertnode(5);
//create loop for testing
obj.createloop(); 
// detect loop
bool a=obj.detectloop(); 
if(a)
cout<<"Loop Found"<<endl;
else
cout<<"Loop not Found"<<endl;

head=NULL;
obj.insertnode(9);
obj.insertnode(10);
obj.insertnode(11);
obj.insertnode(12);
obj.insertnode(13);
bool b=obj.detectloop();
if(b)
cout<<"Loop found"<<endl;
else
cout<<"Loop not found"<<endl;

}

Output:

     Loop Found
     Loop not found

Example of the method

Here is an example of the above method:
let the linked list be 1->2->3->4->2 (here 4 is connected to node 2 to create a cycle).
At first step, put the address of each node into the hash table i.e in this example address of node 1,2,3,4 are put into the hash table.
Now the next of the node 4 has the address of the previously stored node 2.
so the address of 2 is already in the hash table. so it is not stored again and the loop is detected.

Explanation of the Method detect loop

The detect loop method is detecting the loop in the linked list. s.insert() is adding the node into the hash table if the node is traversed for the first time.if the node is already in the hash then s.find(head) != s.end() will return true.if there is no loop the method will return false.

• Time complexity: Big O(n)
• Space complexity: Big O(1)

Floyd's Cycle finding algorithm

This is the fastest method for finding the loop in a linked list.In this approach two pointers are used to detect the cycle.

pseudocode for the method

Here is the working of the algorithm.

• A slow and a fast pointer is used.
• Slow pointer moves by one node and fast pointer moves by two nodes.
• If there is a loop in the linkedlist both the pointers meet at a node else the pointers do not meet.

Implementation of Floyd's Algorithm:

//algorithm  to find the loop in linkedlist
#include<iostream>
using namespace std;
class node
{
  public:
      int data;
      node* next;
};
node* head=NULL;
class Linkedlist
{
    public:
        void insertnode(int value)
        {
            node* new_node=new node();
            new_node->data=value;

            if(head==NULL)
            head=new_node;

            else
            {
                new_node->next=head;
                head=new_node;
            }
        }

        void createloop()
        {
            node* temp=head;
            while(temp->next!=NULL)
            {
                temp=temp->next;
            }
            temp->next=head;
        }
        int detectloop()
        {
            node* slow=head;
            node* fast=head;
            while(slow && fast && fast->next)
            {
                slow=slow->next;
                fast=fast->next->next;
                if(slow==fast)
                {
                    cout<<"Loop Found"<<endl;
                    return 1;
                }

            }


            cout<<"Loop not found"<<endl;
            return 0;
        }
     };
int main()
{
Linkedlist obj;

//insert nodes in linkedlist
obj.insertnode(3);
obj.insertnode(9);
obj.insertnode(7);
obj.insertnode(4);
obj.insertnode(5);

//create loop for testing
obj.createloop(); 

// detect loop
obj.detectloop(); 

//point the head to null to create a new list
head=NULL;

//insert the nodes in list
obj.insertnode(9);
obj.insertnode(10);
obj.insertnode(11);
obj.insertnode(12);
obj.insertnode(13);

//detect if there is a loop
obj.detectloop();

}

Output:

Loop Found 
Loop not found

Explanation and Example of the Method detect loop

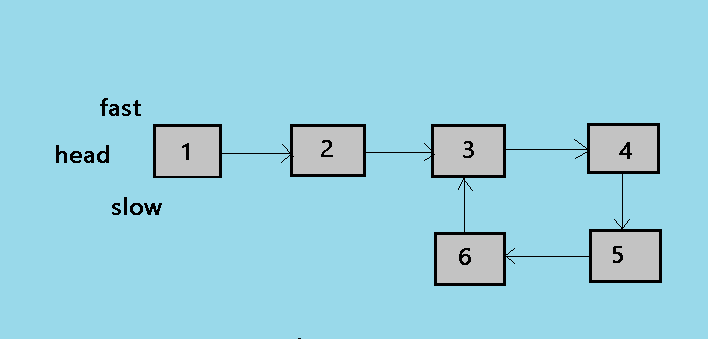
1. This is the initial state of the algorithm, where slow and fast both the pointer points to the head of the linked list.

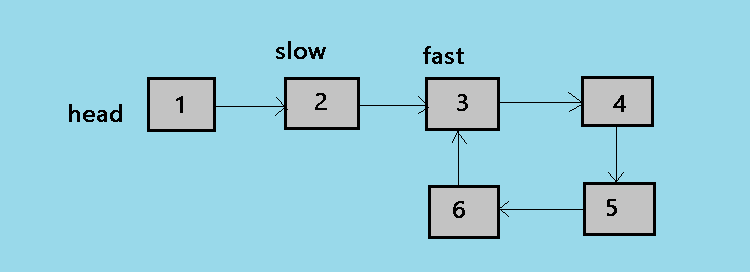
2. At the second step of the algorithm, the slow pointer moves by one node and the fast pointer moves by two nodes. so now slow is at 2 and fast is at 3.

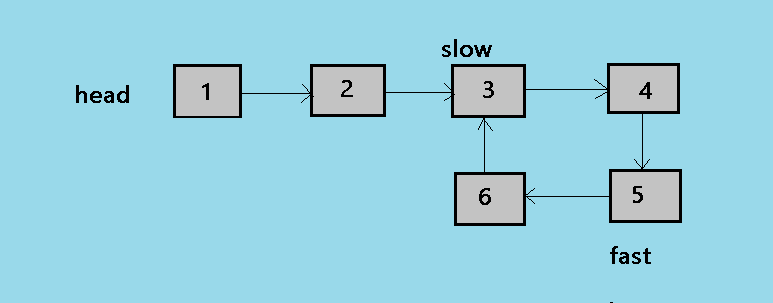
3. At the third step of the algorithm, the loop continues and now slow is at 3 and fast is at 5.

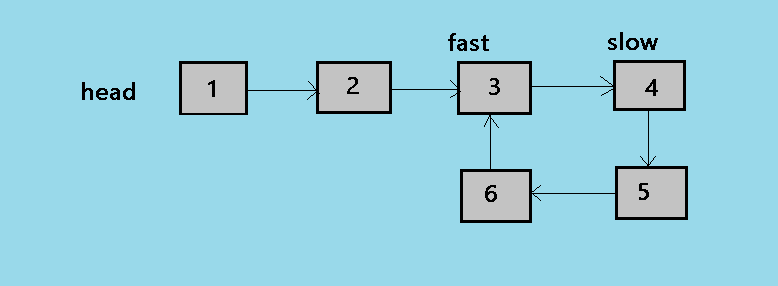
4. At the fourth step of the algorithm, the slow pointer is at 4 and now fast pointer is at 3.

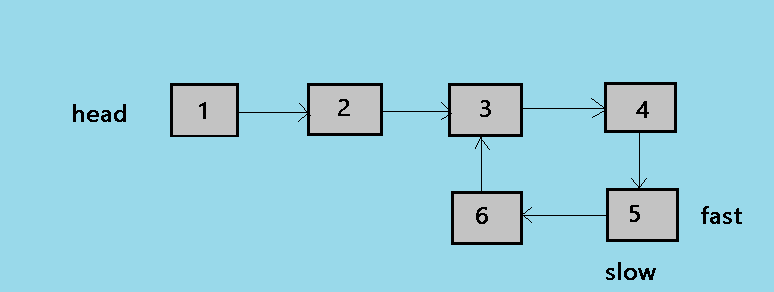
5. This is the fifth and the last step of the algorithm, in this step slow moves by one node and fast moves by two so now both points to the node 5.