
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article we will look at the method of finding the length of a loop in a linked list.For that you should be able to understand the floyd's loop detection algorithm.
Here is a picture that shows the cycle/loop in a linked list with a length of 4.
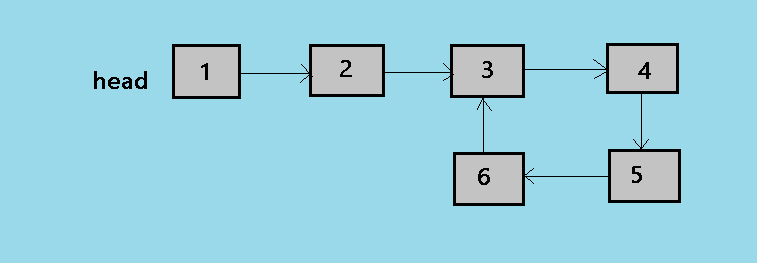
Before we move forward with the length of cycle in a linked list, let's look at the floyd's cycle finding algorithm.
floyd's cycle finding algorithm
Here is the working of the algorithm.
- A slow and a fast pointer is used.
- Slow pointer moves by one node and fast pointer moves by two nodes.
- If there is a loop in the linkedlist both the pointers meet at a node else the pointers do not meet.
According to the the floyd's algorithm the slow and fast pointer will meet at a node in the loop. In this case 3,4,5,6 are the nodes where the pointers can meet.
now let's look at the method in detail.
Length of a loop
To find the length of a loop first we need to find if there is a loop in the linked list.If there is a loop in the linked list then the function should return the length of the linked list. if there is no loop in the linked list then the function will return 0 as the length of the loop will be 0.
pseudocode for the method
- Find the loop using the floyd's algorithm.
- if no loop detected then return 0.
- if the linked list contains loop then store the address of the node where the fast and the slow pointer meet.
- Initilize a counter variable as 1(starting from the current node) and keep on incrementing the counter till we reach the same node again.
Implementation of the method
#include<iostream>
using namespace std;
class node
{
public:
int data;
node* next;
};
node* head=NULL;
class Linkedlist
{
public:
void insertnode(int value)
{
node* new_node=new node();
new_node->data=value;
if(head==NULL)
head=new_node;
else
{
new_node->next=head;
head=new_node;
}
}
void createloop()
{
node* temp=head;
while(temp->next!=NULL)
{
temp=temp->next;
}
temp->next=head;
}
int countlength(node *n)
{
int counter = 1;
node *temp = n;
while (temp->next != n)
{
counter++;
temp = temp->next;
}
return counter;
}
int detectloop()
{
node* slow=head;
node* fast=head;
while(slow && fast && fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
{
return countlength(slow);
}
}
return 0;
}
};
int main()
{
Linkedlist obj;
//insert nodes in linkedlist
obj.insertnode(1);
obj.insertnode(2);
obj.insertnode(3);
obj.insertnode(4);
obj.insertnode(5);
obj.insertnode(6);
//create loop for testing
obj.createloop();
// detect loop
int ans=obj.detectloop();
cout<<"The length of the loop is "<<ans<<endl;
//point the head to null to create a new list
head=NULL;
//insert the nodes in list
obj.insertnode(9);
obj.insertnode(10);
obj.insertnode(11);
obj.insertnode(12);
obj.insertnode(13);
//detect if there is a loop
int ans1=obj.detectloop();
cout<<"The length of the loop is "<<ans1<<endl;
}
Output:
The length of the loop is 4
The length of the loop is 0
Explanation of the method
In the above program first linked list that is 1->2->->4->5->6->3 has a loop of length 4 and the 2nd linked list tkaen is 9->10->11->12->13 with no loop it means that the length of the loop is 0. now let's look at the main functions in the program the detectloop() function detects if there is a loop in the linked list using the floyd's algorithm. we have taken two pointers as slow and fast. slow moves by one node at a time while the fast pointer moves by two nodes at a time.whenever the two pointers meet i.e (slow==fast) becomes true then the slow pointer i.e address of a particular node in he loop is returned to the function countlength(). Now countlength() function counts the length of the loop in the linked list. first we have initilized a counter variable as 1. then we have taken a temp pointer and initilized it with the slow pointer. now traverse the loop again till the next of the current node is not is not equal to the temp(the starting node of the traversal). we keep on increasing the counter variable as we traverse the loop. and the final value of the length of loop(counter) is returned when the loop breaks.
If there is no loop in the linked list then the function detectloop() will return 0 as the there is no loop and the length of the loop will be 0. as in the case of our second linked list 9->10->11->12->13.
Example of the method
For example the linked list be 1->2->3->4->5->6->3(as shown in the above image).
now apply the floyd's algorithm on the given list.For more the detailed explanation of the floyd's algorithm have a look at the "Detect a loop in linked list" article.
Below is the last step of the algorithm here slow and fast both the pointers point to the node 5.
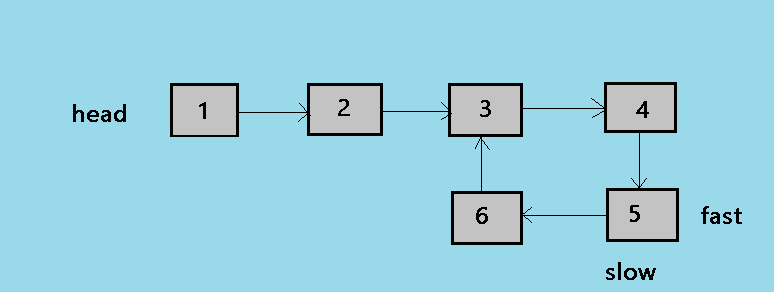
Now return the slow pointer to the function countlength() take the variable counter=1 and traverse the loop again till the slow pointer is reached again. keep on increasing the counter variable and return it when the loop is breaked.
