Cycle Detection Algorithms

As we have already seen various algorithms to detect a cycle in a linked list. In this article we are going to explore some more cycle detection algorithms in general.

A cycle in a data structure as we have already seen is a condition with no end.
Here are a few popular cycle detection algorithms:

• Floyd's cycle detection algorithm
• Brent’s Cycle Detection Algorithm

Both of these algorithms are used to find the cycle in a linked list.Both of the algorithms use the slow and fast pointer approach but implementation is different. before we go into the details of these methods, let's look at the major differences between these two algorithms.

Difference between Floyd's and Brent's Algorithm

1. Brent's Algorithm Finds the length of loop in with cycle detection loop itself. No need to traverse the loop again for counting the nodes in the loop.
2. Brent's Algorithm is faster than Floyd's algorithm.
3. Time complexity of Brent's Algorithm is big o(m+n). while Floyd's algorithm complexity is big o(n).

Brent's Algorithm

Brent's cycledetection algorithm is similar to floyd's cycle detection algorithm as both the approaches use two pointes but there is a difference between the two approaches. Here we make one pointer halted till every iteration and move it to other pointer at every power of two. The smallest power of two where the two pointers meet is the starting point of the cycle.

Pseudocode for the algorithm

1. Move fast pointer in powers of 2 till we find a loop. After every power, we reset slow pointer to previous value of fast pointer. Reset length to 0 after every power.
2. The condition for loop testing is slow and fast become same as in the floyd's algorithm and if there is no loop then the fast pointer points to null after the loop is terminated.
3. If there is a loop then when we come out of the loop we have the length of the loop as well.
4. We reset slow pointer to head pointer and fast pointer to node at position head + length.
5. Beginning of loop can be found by moving both the pointers one by one.

Code for the Brent's algorithm

#include<iostream>
using namespace std;


class Node { 
public:
int data; 
Node* next; 
}; 

Node* detectCycle(Node* head) 
{ 
// if head is null then no loop 
if (head == NULL)  
    return NULL;     

Node* slow = head; 
Node* fast = head->next; 
int power = 1; 
int length = 1; 

while (fast != NULL && fast != slow)
{ 


    if (length == power) { 

        // updating the power. 
        power *= 2; 

        // updating the length 
        length = 0; 

        slow = fast; 
    } 

    fast = fast->next; 
    ++length; 
} 

// if it is null then no loop 
if (fast == NULL)  
    return NULL;     

// length stores actual length of the loop.

// Now set slow to the beginning 
// and fast to head+length i.e length of the cycle. 
slow = fast = head; 
while (length > 0) { 
    fast = fast->next; 
    --length; 
} 

// Now move both pointers by one node so that they meet at the beginning loop. 
while (fast != slow) { 
    fast = fast->next; 
    slow = slow->next; 
} 

return slow; 
} 

Node* newNode(int key) 
{ 
    Node* temp =  new Node();
    temp->data = key; 
    temp->next = NULL; 
    return temp; 
} 

// Driver program to test above function 
 int main() 
{ 
    Node* head = newNode(1); 
    head->next = newNode(2); 
    head->next->next = newNode(3); 
    head->next->next->next = newNode(4); 
    head->next->next->next->next = newNode(5); 

    // Create a loop for testing  
    head->next->next->next->next->next =  
                          head->next->next; 

    Node *res = detectCycle(head); 

    if (res == NULL) 
       cout<<"NO LOOP"<<endl;
    else
        cout<<"LOOP IS AT "<< res->data;
    return 0; 
} 

output:

LOOP IS AT 3 

Explanation

detectCycle() function detects the loop in the list If loop was there in the list then it returns, the first node of loop otherwise returns NULL. The while loop in the function returns NULL if there is no loop else it will return the first node in the loop.the if condition in the while loop determines the condition after which we will update the power and length as smallest power of two this gives us the starting node in the cycle if there is cycle in the loop.
The code gives us the length of the loop as well if we want we can print the length of the loop too.
the function returns the slow pointer .i.e the starting point of the loop if there is loop and NULL if there is no loop.
the function calculates the length of the loop as well in the above code we have not returned the value of the length variable if required we can print or return the length of the loop as well.
then in the main function we have created a loop for the testing if our code is working fine or not. the output of the above code is "LOOP IS AT 3" (without the quotes).

• Time complexity: Big O(M+N)
  M is the beginning of a cycle and N is the length of the loop.
• Space complexity: Big O(1)

Floyd's cycle finding algorithm

As we have already discussed earlier about the floyd's algorithm , it uses the same approach as brent's (the approach of two pointers slow and fast pointer).This algorithm does not gives us the length of the loop and the starting point of the loop. The Floyd's Algorithm only detects the loop and returns a particular node in the loop (not necessarily the first node in the loop).
The brent's algorithm is a better approach than the floyd's algorithm and it also gives the starting node as well as the length of the loop whereas the floyd's algorithm does not gives the length and the starting node of the cycle.
here is the pseudocode for the floyd's algorithm.

pseudocode for the method

Here is the working of the algorithm.

• A slow and a fast pointer is used.
• Slow pointer moves by one node and fast pointer moves by two nodes.
• If there is a loop in the linkedlist both the pointers meet at a node else the pointers do not meet.

Implementation of Floyd's Algorithm:

//algorithm  to find the loop in linkedlist
#include<iostream>
using namespace std;
class node
{
  public:
      int data;
      node* next;
};
node* head=NULL;
class Linkedlist
{
    public:
        void insertnode(int value)
        {
            node* new_node=new node();
            new_node->data=value;

            if(head==NULL)
            head=new_node;

            else
            {
                new_node->next=head;
                head=new_node;
            }
        }

        void createloop()
        {
            node* temp=head;
            while(temp->next!=NULL)
            {
                temp=temp->next;
            }
            temp->next=head;
        }
        int detectloop()
        {
            node* slow=head;
            node* fast=head;
            while(slow && fast && fast->next)
            {
                slow=slow->next;
                fast=fast->next->next;
                if(slow==fast)
                {
                    cout<<"Loop Found"<<endl;
                    return 1;
                }

            }


            cout<<"Loop not found"<<endl;
            return 0;
        }
     };
int main()
{
Linkedlist obj;

//insert nodes in linkedlist
obj.insertnode(3);
obj.insertnode(9);
obj.insertnode(7);
obj.insertnode(4);
obj.insertnode(5);

//create loop for testing
obj.createloop(); 

// detect loop
obj.detectloop(); 

//point the head to null to create a new list
head=NULL;

//insert the nodes in list
obj.insertnode(9);
obj.insertnode(10);
obj.insertnode(11);
obj.insertnode(12);
obj.insertnode(13);

//detect if there is a loop
obj.detectloop();

}

Output:

Loop Found 
Loop not found

Explanation and Example of the Method detect loop

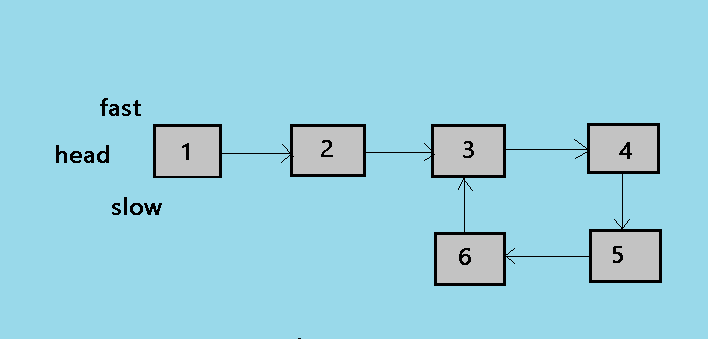
1. This is the initial state of the algorithm, where slow and fast both the pointer points to the head of the linked list.

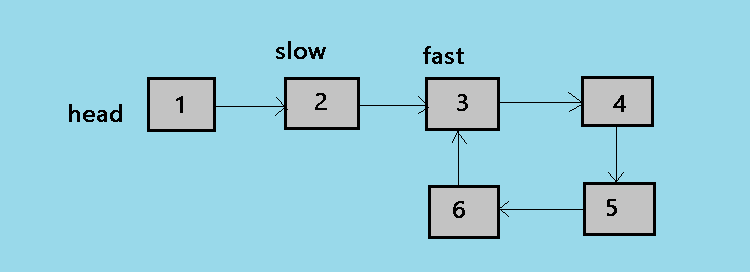
2. At the second step of the algorithm, the slow pointer moves by one node and the fast pointer moves by two nodes. so now slow is at 2 and fast is at 3.

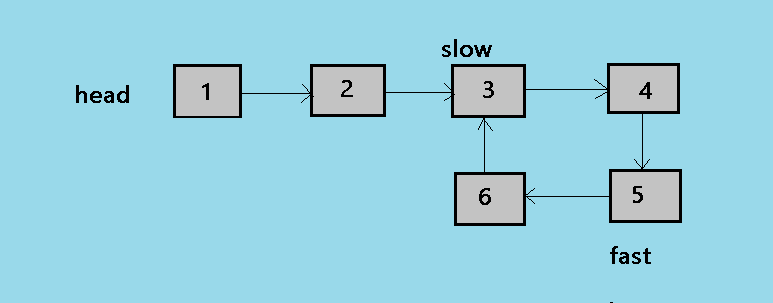
3. At the third step of the algorithm, the loop continues and now slow is at 3 and fast is at 5.

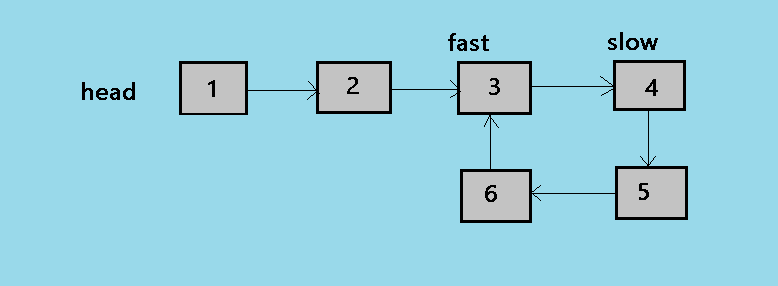
4. At the fourth step of the algorithm, the slow pointer is at 4 and now fast pointer is at 3.

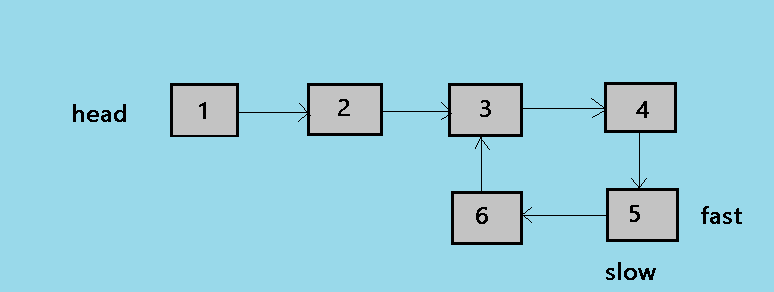
5. This is the fifth and the last step of the algorithm, in this step slow moves by one node and fast moves by two so now both points to the node 5.