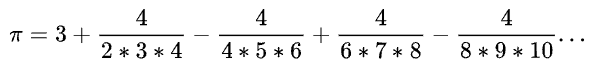In this article, we have covered different algorithms and approaches to calculate the mathematical constant pi (3.14159...). These include Nilakantha Series, Leibniz’s Formula, Ramanujan's Pi Formula and other Programming Language specific techniques.

Table of contents:

1. Method 1: Leibniz’s Formula
2. Method 2: Nilakantha Series
3. Method 3: Ramanujan's Pi Formula
4. Method 4: Function acos()
5. Method 5: Math module
6. Method 6: gmpy module

We will get started with Different ways to calculate Pi (3.14159...).

Method 1: Leibniz’s Formula

This equation can be implementd in any programming language.
Accuracy of value of pie depends on number of terms present in the equation which means high number of iterations produce better result.

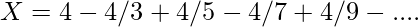
Implementation of Leibniz’s Formula:

1. We will create 2 variables sum, d (denominator)
2. Initialise sum = 0
3. Initialise d = 1
4. Create a for loop
5. Loop i from 0 to 1000000 ( bigger number = more precsion )
6. Check if i is even then sum=sum+4/d, else sum=sum-4/d
7. Increment d by 2 every at every iteration
8. Print sum

Time Complexity:

O(N * logN * loglogN), where

• N = number of iterations
• Division of two numbers of order O(N) takes O(logN loglogN) time.

Code:

    #Initialize denominator
    d = 1
    #Initialize sum
    sum = 0
 
    for i in range(0,1000000):
 
       #even index add to sum
       if i % 2 == 0:
           sum + = 4/d
       else:
       #odd index subtract from sum
           sum -= 4/d
 
    #increment denominator by 2 
    d += 2
    
    print("Value of Pi is : ",sum)

Sample Output:

   Value of Pi is : 3.1415916535897743

Method 2: Nilakantha Series

It is somewhat similar to the previous method and also one of the conventional methods. As number of iterations increases the value of pi also gets precise.

Implementation:

1. Create 3 variables n,sum,sign
2. Initialse sum=3, n=2, sign=1
3. Create a for loop
4. loop from 0 to 1000000
5. At every iteration multiply sign=sign*(-1)
6. Calculate sum=sum+sign*(4/(n)*(n+1)*(n+2))
7. Increment n by 2 at every iteration
8. Print sum

Time Complexity:

O(N * logN * loglogN), where

• N = number of iterations
• Time Complexity of multiplication and division is O(logN loglogN) at the best and O(logN logN) in general.

Code:

   #Initialise sum=3,n=2,and sign=1
   sum=3
   n=2
   sign=1
   
   #for loop to add terms
   for i in range(0,1000000):
       
       sum=sum+(sign*(4/((n)*(n+1)*(n+2))))
       
       #for addition and subtraction of alternate terms
       sign=sign*(-1) 
       
       #Increment by 2 according to formula
       n=n+2
       
   print("Value of Pi is : ",sum)

Sample Output:

   Value of Pi is : 3.141592653589787

Method 3: Ramanujan's Pi Formula

Ramanujan's Pi formula is one of the best methods to find numerical approximation of pi in less number of iterations. It may look difficult to implement but that is not the case, it's pretty simple, just follow these steps.

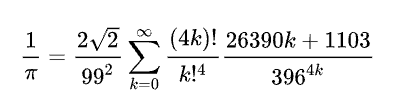
Implementation:

1. Firstly import math module
2. Create function to calculate factorial
3. Create function to calculate Pi by Ramanujan's Formula
4. Initialise sum=0,n=0,i=math.sqrt(8)/9801
5. Start the infinite while loop
6. Apply Ramanujan's Formula
7. Add the value to sum+=tmp
8. At every iteration increase n by 1, n=n+1
9. If the value has reached femto level that is 15th digit break the loop
10. Return 1/sum according to the formula
11. Print the value of sum

Time Complexity:

O(N² logN loglogN), where

• N = number of iterations
• Time Complexity of multiplication and division is O(logN loglogN) at the best and O(logN logN) in general.

Though the Time Complexity is higher than previous approaches, in this approach, one will need significantly less number of iterations so this is considered to be an effective technique.

Code

   import math

   #finds factorial for given number
   def factorial(x):
       if x==0:
           return 1
       else:
           return r = x*factorial(x-1)
        
   #Ramanujan formula for pi calculation
   def ramanujan_pi():

       #initialise sum=0, n=0 , and a variable i  to store 2√2/(99)^2
       sum = 0
       n = 0
       i = (math.sqrt(8))/9801

      while True:
           #Ramanujan's Formula:-
           tmp = i*(factorial(4*n)/pow(factorial(n),4))   ((26390*n+1103)/pow(396,4*n))
           sum +=tmp
        
           #Stop loop when it reaches 15th digit precision (femto)
           if(abs(tmp) < 1e-15):
               break
           n += 1

       return(1/sum)

   print("Vaule of Pi is : ",ramanujan_pi())

Sample Output

   Vaule of Pi is : 3.141592653589793 

Method 4: Function acos()

acos() is an inbuilt function in C++ STL and is also present python language and it’s the same as the inverse of cosine in maths. The acos() function returns the values in the range of [-π,π] that is an angle in radian. It can only show till 15th digit precison.

Implementation

1. Import acos from math library
2. Define the function to take input n the number of decimal places
3. Use round function to get the pi value to desired decimal place
4. Use formula pi=round(2*acos(0.0),n)
5. Print value of by calling the function pi

Time Complexity

O(1)

Code:

   #Import acos from math
   from math import acos
   
   #define function
   def valueofpi(n):
         
         #Calculates pi with precision n, where n<=15
         pi=round(2*acos(0.0),n)
         
         #prints pi with n precision
         print(pi)
         
   print("Value of Pi is : ",valueofpi(15))
         

Sample Output:

   Value of Pi is : 3.141592653589793

Method 5: Math module

This is one of the simplest method to get the value of Pi without much hassle, it saves a lot of time.
Directly get the value of pi by using math module in python.
One drawback is that you can not get as precise result as the previous methods would provide.

Time Complexity:

O(1)

Code:

   #import math module
   import math
   
   #print value
   print("Value of Pi is : ",math.pi )
   

Sample Output:

   Value of Pi is : 3.141592653589793

Method 6: gmpy module

This is the best option in most of the cases , you can directly get the value of pi upto your desired precison with this module.
It is the better version of math module and nmpy module for calculating pi.

Time Complexity:

O(1)

Code:

   #import gmpy module
   import gmpy
   
   #print value upto 128 bit precision
   #Note that it takes argument in bits not in decimal digits
   print ("Value of Pi is : ",gmpy.pi(128))
   

Sample Output:

Value of Pi is : 3.1415926535897932384626433832795

With this article at OpenGenus, you must have the complete idea of different approaches to find the value of Pi.