What is a Disarium Number?

A disarium number is a number in which the sum of the digits to the power of their respective position is equal to the number itself (position is counted from left to right starting from 1).

Example of a Disarium number is 175,
1¹ + 7² + 5³ = 1 + 49 + 125= 175
Hence,175 is a disarium number.

Our approach will be straightforward. We will break the number into digits and then power it with their respective position and then add it to check if the obtained sum equals the given number.

Psuedo Code for the Algorithm

where 'num' is the given number to check for disarium number.

START
DEFINE num= 135
SET sum= 0, rem= 0
len= calcLength(num)
SET n= num
    while (n > 0)
        rem = n%10
        sum = sum + (rem*len)
        n = n/10
        len--
    end while

    if(sum == num) then 
        PRINT "Yes" 
    else 
        PRINT "No"
END

To obtain the length of the number

calcLength(num)

START
SET length= 0
    while (num > 0)
        length = length+1
        num = num/10

RETURN length
END

Implementation in C++

Following is our C++ implementation of checking the Disarium Number:

// A C++ program to check for Disarium Number 
#include <iostream>
#include <bits/stdc++.h>
using namespace std;

//calcLength() will count the digits present in a number    
int calcLength(int n) {
     int length= 0;
     while(n > 0) {
         length++;
         n= n/10;
     }
     
     return length;
}

int main()
{
     int num= 135, sum= 0, rem= 0;
     int len= calcLength(num);

     //Makes a copy of the original number num
     int n= num;

     //Calculates the sum of digits powered with their respective position
     while(n > 0) {
         rem= n%10;
         sum= sum + pow(rem, len);
         n= n/10;
         len--;
     }
     
     // Check whether sum is equal to the given number
     if(sum == num)
         cout<<num<<" is a Disarium Number";
     else
         cout<<num<<" is not a Disarium Number";
         
    return 0;
}

Workflow of solution

1. calcLength() is used to obtain the length of the number. It will divide (integer division is taken, not decimal) the number by 10 until it becomes 0. Along with it, each time, the length variable is incremented.
Example- to check length of 352, let length= 0
352 > 0, then length= 1 and 352/10= 35
35 > 0, then length= 2 and 35/10= 3
3 > 0, then length= 3 and 3/10= 0
0 > 0, it is false therefore terminate the loop and length= 3.

2. In the main(), we will make the copy (let n) of the original number (let num) as we will use the copy to calculate the sum. We will calculate the number raised to its position by getting the unit place digit from the right position and raised to the number's length.
a. We will break the number till the copy of the number (n) become 0 and find the unit digit by getting the remainder (let rem) when divide by 10.
b. We will use the remainder to find the remainder raised to its position. The position is the current length of the number.
c. Then divide the n by 10 to find the next unit place digit and decrement the length representing the updated unit place digit position.

Similar approach but using Recursion

Now, you have an idea of how the Disarium Number is calculated. Let's now see another approach using recursion.
In the above solution, we used a loop to break the unit place digit and decrement the length. Now that work will be done in the recursion.

Working of Recursion approach

The approach is very much similar to the above solution. Firstly, we obtain the length of the number, and in this approach, we break the unit place digit and raise it to its position in power and then pass the remaining number to the next recursion step.
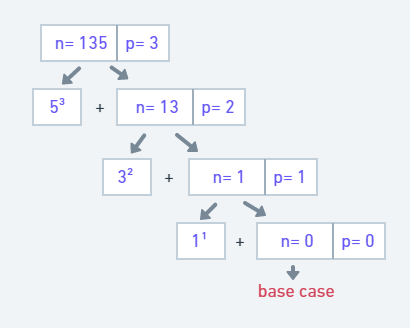
For example, let the number= 135 and length=3, we then break the 5 and raise it to the power of 3 and then pass number= 13 and length=2 to the next recursion step, and its result will be added to the result of 5³ to calculate the sum. The recursion process will work till the number is not zero. It will act as a base case to return 0 when the number becomes 0, and the returned value is the sum of the digit raised to its respective position.
The returned value will be compared with the original number to check for the Disarium number.

The recursion process can be seen below,

Implementation in C++

Following is our C++ implementation of checking the Disarium Number using recursion:

// A C++ program to check for Disarium Number using Recursion
#include <iostream>
#include <bits/stdc++.h>
using namespace std;

// Recursion process to calculate the sum of the digit raised to its respective position
int sumOfDigits(int num, int p) {
    if(num == 0)
        return 0;

    else
        return pow((num%10), p) + sumOfDigits(num/10, p-1);
}

//calcLength() will count the digits present in a number 
int calcLength(int n) {
    int length= 0;
    while(n > 0) {
        length++;
        n= n/10;
    }

    return length;
}


int main()
{
    int num= 175, sum= 0, rem= 0;
    int len= calcLength(num);

    // Check wheter sum is equal to the given number
    if(sumOfDigits(num, len) == num)
        cout<<num<<" is a Disarium Number";
    else
        cout<<num<<" is not a Disarium Number";
 
    return 0;
}

With this, you must have the clear idea of Disarium Number. Enjoy.