Reading time: 40 minutes | Coding time: 10 minutes

In this article, we will explore FisherFaces techniques of Face Recognition. FisherFaces is an improvement over EigenFaces and uses Principal Component Analysis (PCA) and Linear Discriminant Analysis (LDA).

The general steps involved in face recognition are :

1. Capturing
2. Feature extraction
3. Comparision
4. Match/non-match

OpenCV has three built-in face recognizers. We can use any of them by a single line of code. The recognisers are :

• EigenFaces – cv2.face.createEigenFaceRecognizer()
• FisherFaces – cv2.face.createFisherFaceRecognizer()
• Local Binary Patterns Histograms (LBPH) – cv2.face.createLBPHFaceRecognizer()

In this article, we will focus on FisherFaces.

As FisherFaces is an improvement over EigenFaces, we will go through some basic background on EigenFaces before going into FisherFaces so that the process is clear.

Basic background on EigenFaces

This algorithm follows the concept that all the parts of face are not equally important or useful for face recognition . When we look at a face we look at the places of maximum variation so that we can recognise that person . For example from nose to eyes there is a huge variation in everyone's face. Eigenfaces algorithm works at the same principle .

Eigenfaces algorithm works at the same principle . It takes all training faces of all people at once and looks at them as a whole an then it keeps the most important components and disards the rest. These important components are known as principle components.
PCA method is less optimal in the separation between classes.

Due to the useful features of faces this algorithm uses it's known as eigen faces. But this algorithm also considers illumination as an important factor. So as it picks up light illuminations it considers it as a feature representing a face which is not true.

This algorithm doesn't pay attention to the features that differentiate one individual from another. It just concentrates on the features that represent all the faces of all the people.

So, to overcome problems of eigenfaces, Fisherfaces was introduced which iss an improved version of eigenfaces algorithm.

FisherFaces

So, we know that eigenfaces considers illumination an important feature of a face but it actually isn't.

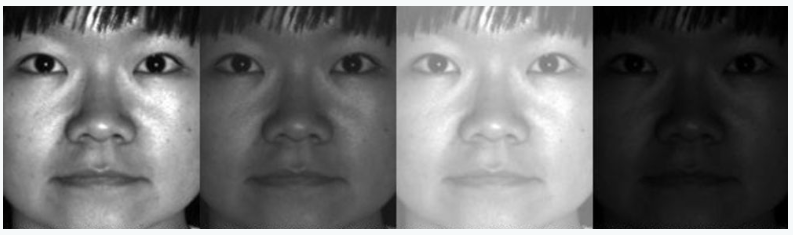
Considering these illuminations as an important feature it may discard other people's features considering them less useful.

We can fix this by tuning eigenfaces such that it extracts features of all individuals separately instead of looking at them as a whole. So, now even if one person's face data has high illumination changes, it will not affect other people's features.

Fisherfaces algorithm extracts principle components that separates one individual from another. So , now an individual's features can't dominate another person's features.

Image recognition using this algorithm is based on reduction of face space domentions using PCA method and then applying LDA method also known as Fisher Linear Discriminant (FDL) method to obtain characteristic features of image.

LDA is used to find a linear combination of features that separates two or more classes or objects. It can be used for dimension reduction before further classification. It attempts to model the difference between classes of data .

This method doesn't capture illumination variations as obviously as Eigenfaces method.

• Data is assumed to be uniformly distributed in each class.
• Aim is to maximize the ratio of between-class scatter matrix and the within-class scatter matrix.
• It can produce good results even in varying illumination.

Algorithm of FisherFaces

Let X be a random vector with samples drawn from c classes:

The scatter matrices S_{B} and S_{W} are calculated as:

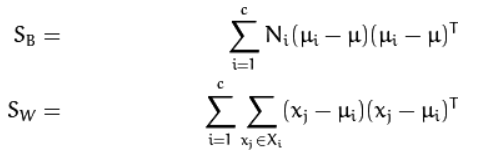
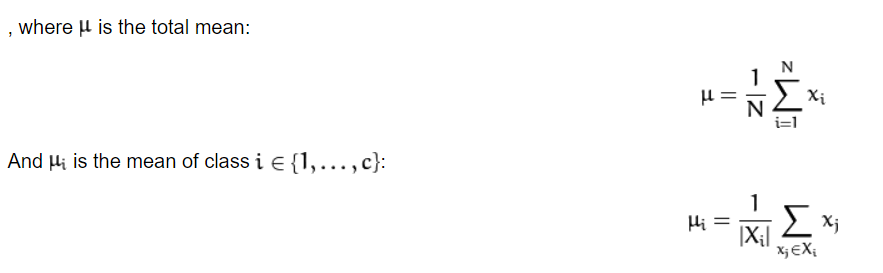
Fisher’s classic algorithm now looks for a projection W, that maximizes the class separability criterion:

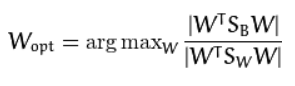
A solution for this optimization problem is given by solving the General Eigenvalue Problem:

The optimization problem can then be rewritten as:

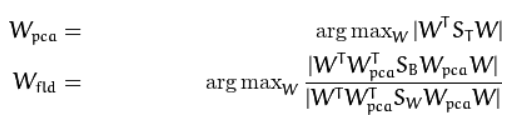
The transformation matrix W, that projects a sample into the (c-1)-dimensional space is then given by:

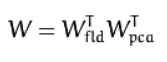
Pseudocode of FisherFaces

def fisherfaces (X ,y , num_components =0) :
    y = np . asarray (y)
    [n , d] = X . shape
    c = len ( np . unique (y ))
    [ eigenvalues_pca , eigenvectors_pca , mu_pca ] = pca (X , y , (n -c ))
    [ eigenvalues_lda , eigenvectors_lda ] = lda ( project ( eigenvectors_pca , X , mu_pca ) , y ,
    num_components )
    eigenvectors = np . dot ( eigenvectors_pca , eigenvectors_lda )
    return [ eigenvalues_lda , eigenvectors , mu_pca ]

Image data

'Yale face database' is used here for training. This database contains many grayscale images of different face poses of many individuals .

Here are the examples of some training images:

Here are the examples of testing data:

FisherFaces Process

Step 1 : Retreive data

Collection of data is done in form of face images . Collection can be done using photographs already saved or from a webcam. Face must be fully visible and must be facing forward.

Step 2 : Image Processing

a) Preprocessing stage : Getting images using camera or saved images and conversion from RGB to grayscale. Image data is divided into training and test data.

b) Processing stage : Fisherface method will be applied to generate feature vector of facial image data used by system and then to match vector of traits of training image with vector characteristic of test image using euclidean distance formula

Step 3 : Feature generation

Features of the faces are extracted.

Recognition process

After the training is done, the next stage is image recognition process. The goal is to successfully recognize the test image.

• If training image is the same as the testing image:
  In this case system can successfully identify the test image correctly up to 100%.

• If training image is not the same as the testing image:
  The test image and the training image must come from the image of the same person's face. System can now successfully identify the test image correctly upto 90%.

Implementation of FisherFaces

First we will implement functions for PCA and LDA

PCA:

def pca (X , y , num_components =0) :
    [n , d] = X . shape
    if ( num_components <= 0) or ( num_components >n) :
        num_components = n
    mu = X. mean ( axis =0)
    X = X - mu
    if n > d:
        C = np . dot (X.T ,X)
        [ eigenvalues , eigenvectors ] = np . linalg . eigh (C)
    else :
        C = np . dot (X ,X .T)
        [ eigenvalues , eigenvectors ] = np . linalg . eigh (C)
        eigenvectors = np . dot (X .T , eigenvectors )
        for i in xrange (n):
            eigenvectors [: , i ] = eigenvectors [: , i ]/ np . linalg . norm ( eigenvectors [: , i ])
    # or simply perform an economy size decomposition
    # eigenvectors , eigenvalues , variance = np. linalg . svd (X.T, full_matrices = False )
    # sort eigenvectors descending by their eigenvalue
    idx = np . argsort ( - eigenvalues )
    eigenvalues = eigenvalues [ idx ]
    eigenvectors = eigenvectors [: , idx ]
    # select only num_components
    eigenvalues = eigenvalues [0: num_components ]. copy ()
    eigenvectors = eigenvectors [: ,0: num_components ]. copy ()
    return [ eigenvalues , eigenvectors , mu ]

LDA:

def lda (X , y , num_components =0) :
    y = np . asarray (y)
    [n , d] = X . shape
    c = np . unique ( y)
    if ( num_components <= 0) or ( num_component >( len (c) -1) ):
        num_components = ( len (c) -1)
    meanTotal = X. mean ( axis =0)
    Sw = np . zeros ((d , d) , dtype = np . float32 )
    Sb = np . zeros ((d , d) , dtype = np . float32 )
    for i in c:
        Xi = X[ np . where (y == i) [0] ,:]
        meanClass = Xi . mean ( axis =0)
        Sw = Sw + np . dot (( Xi - meanClass ).T , ( Xi - meanClass ))
        Sb = Sb + n * np . dot (( meanClass - meanTotal ).T , ( meanClass - meanTotal ))
    eigenvalues , eigenvectors = np . linalg . eig ( np . linalg . inv ( Sw )* Sb )
    idx = np . argsort ( - eigenvalues . real )
    eigenvalues , eigenvectors = eigenvalues [ idx ] , eigenvectors [: , idx ]
    eigenvalues = np . array ( eigenvalues [0: num_components ]. real , dtype = np . float32 , copy =
    True )
    eigenvectors = np . array ( eigenvectors [0: ,0: num_components ]. real , dtype = np . float32 ,
    copy = True )
    return [ eigenvalues , eigenvectors ]

The functions to perform a PCA and LDA are now defined, so we can go ahead and implement the Fisherfaces .

def fisherfaces (X ,y , num_components =0) :
    y = np . asarray (y)
    [n , d] = X . shape
    c = len ( np . unique (y ))
    [ eigenvalues_pca , eigenvectors_pca , mu_pca ] = pca (X , y , (n -c ))
    [ eigenvalues_lda , eigenvectors_lda ] = lda ( project ( eigenvectors_pca , X , mu_pca ) , y ,
    num_components )
    eigenvectors = np . dot ( eigenvectors_pca , eigenvectors_lda )
    return [ eigenvalues_lda , eigenvectors , mu_pca ]

For the Fisherfaces method a similar model to the EigenfacesModel must be defined.

class FisherfacesModel ( BaseModel ):
    def __init__ ( self , X= None , y= None , dist_metric = EuclideanDistance () , num_components
    =0) :
        super ( FisherfacesModel , self ). __init__ (X=X ,y=y , dist_metric = dist_metric ,
    num_components = num_components )
    def compute ( self , X , y):
        [D , self .W , self . mu ] = fisherfaces ( asRowMatrix (X ) ,y , self . num_components )
        # store labels
        self .y = y
        # store projections
    for xi in X :
        self . projections . append ( project ( self .W , xi . reshape (1 , -1) , self . mu ))

Once the FisherfacesModel is defined, it can be used to learn the Fisherfaces and generate predictions.
We are using 'Yale face database' as training data. We can also split the data to use it for testing as well.

import sys
# append tinyfacerec to module search path
sys . path . append ("..")
# import numpy
import numpy as np
# import tinyfacerec modules
from tinyfacerec . util import read_images
from tinyfacerec . model import FisherfacesModel
# read images( from the folder containing yalefaces data )
[X , y] = read_images ("yalefaces_recognition ")
# compute the eigenfaces model
model = FisherfacesModel ( X [1:] , y [1:])
# get a prediction for the first observation
print " expected =", y [0] , "/", " predicted =", model . predict ( X [0])

RESULTS

NOTE

• By using Fisherfaces we can prevent features of an individual from being dominant but it still considers illumination an important feature. But we know that illumination is not an important feature as it's not even a part of face.
• PCA dimension reduction process can cause some loss of discriminant information useful in the LDA process which is a disadvantage of this process.
• The problem of computation in face recognition using fisherface method is because the computation process is very complicated and complex.

It can be fixed by using LBPH algorithm. It doesn't look at image as a whole, but instead tries to find its local structure by comparing each pixel to its neighboring pixels.

Conclusion

• Fisherfaces method is immune to noise-induced images and the blurring effect on the image.
• Features of an individual cannot dominate other person's features in Fisherfaces.