Fully Connected Layer: The brute force layer of a Machine Learning model

Fully Connected layers in a neural networks are those layers where all the inputs from one layer are connected to every activation unit of the next layer. In most popular machine learning models, the last few layers are full connected layers which compiles the data extracted by previous layers to form the final output. It is the second most time consuming layer second to Convolution Layer.

The diagram below clarifies the statement.

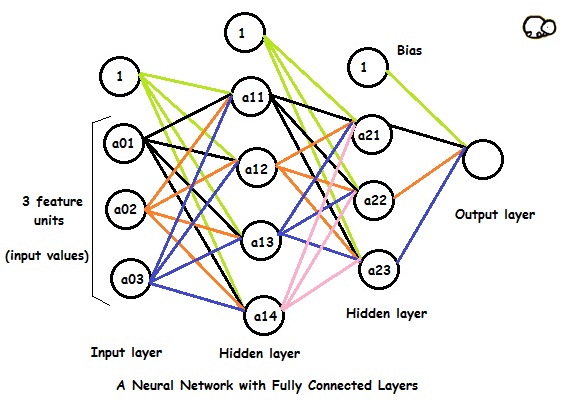
In the above model:

• The first/input layer has 3 feature units and there are 4 activation units in the next hidden layer.
• The 1's in each layer are bias units.
• a01, a02 and a03 are input values to the neural network.They are basically features of the training example.
• The 4 activation units of first hidden layer is connected to all 3 activation units of second hidden layer The weights/parameters connect the two layers.

So the activation units would be like this:

Theta00, theta01 etc. are weights in the above picture. A conventional neural network is made up of only fully connected layers. Whereas in a Convolutional Neural Network, the last or the last few layers are fully connected layers.

Let’s take a simple example of a Neural network made up of fully connected layers.

Example of AND and OR boolean expression

Before moving on to the main example, let us see two small examples of neural networks computing AND and OR boolean operation.

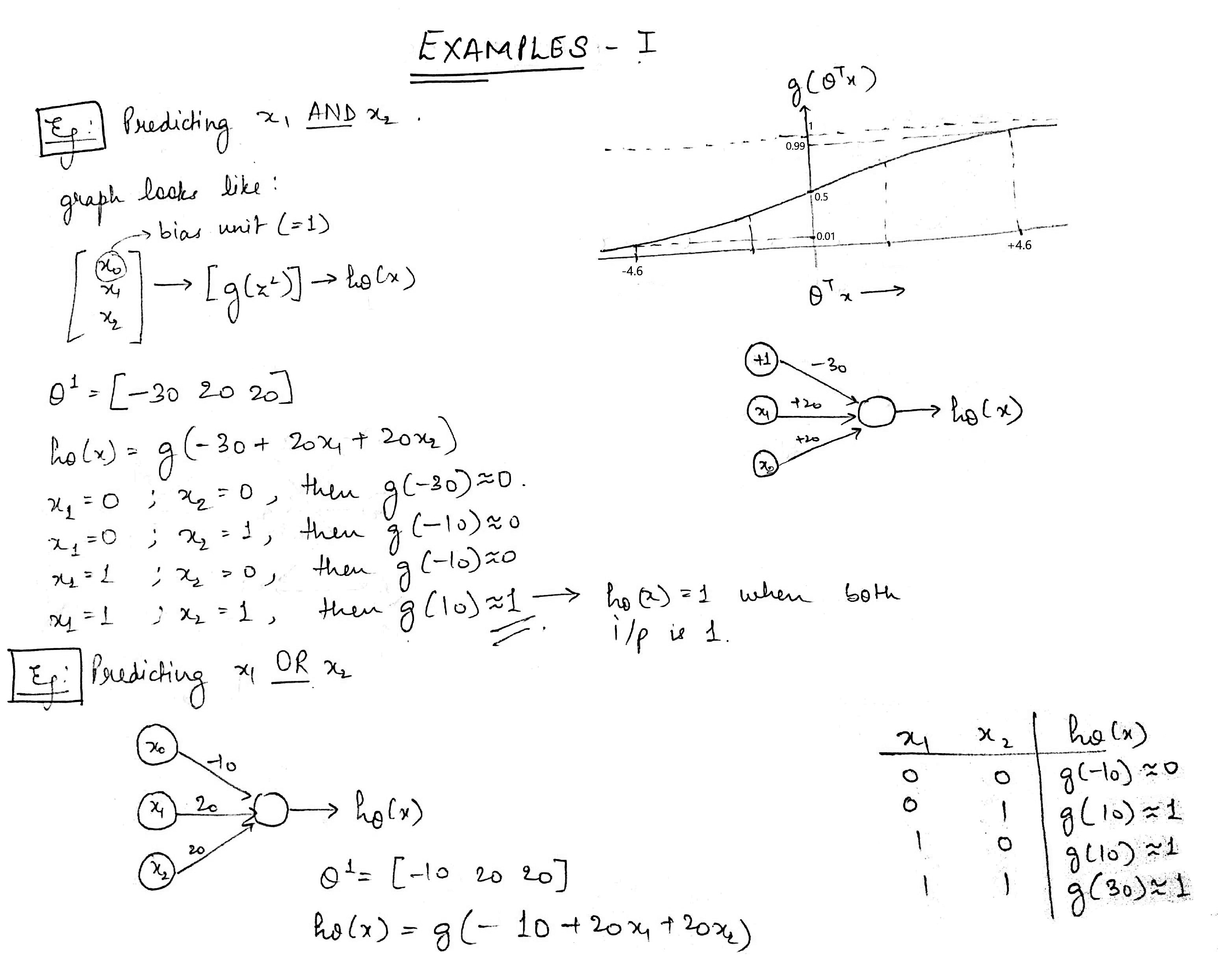
Key points:

• As you can see in the graph of sigmoid function given in the image, g(x) where x>4.6 is almost equal to 1 and g(x) where x < 4.6 is almost equal to 0.
• The x0(= 1) in the input is the bias unit. Every layer has a bias unit.
• h(subscript theta) is the output value and is equal to g(-30 + 20x1 +20x2) in AND operation.
• As you can see in the first example, the output will be 1 only if both x1 and x2 are 1.
• In the second example, output is 1 if either of the input is 1.
• The weights have been pre-adjusted accordingly in both the cases.
• In actual scenario, these weights will be ‘learned’ by the Neural Network through backpropagation.

Example of XNOR neural network

Let us now move to the main example. We will predict x1 XNOR x2. The prediction should be 1 if both x1 and x2 are 1 or both of them are zero.

See the diagram below:

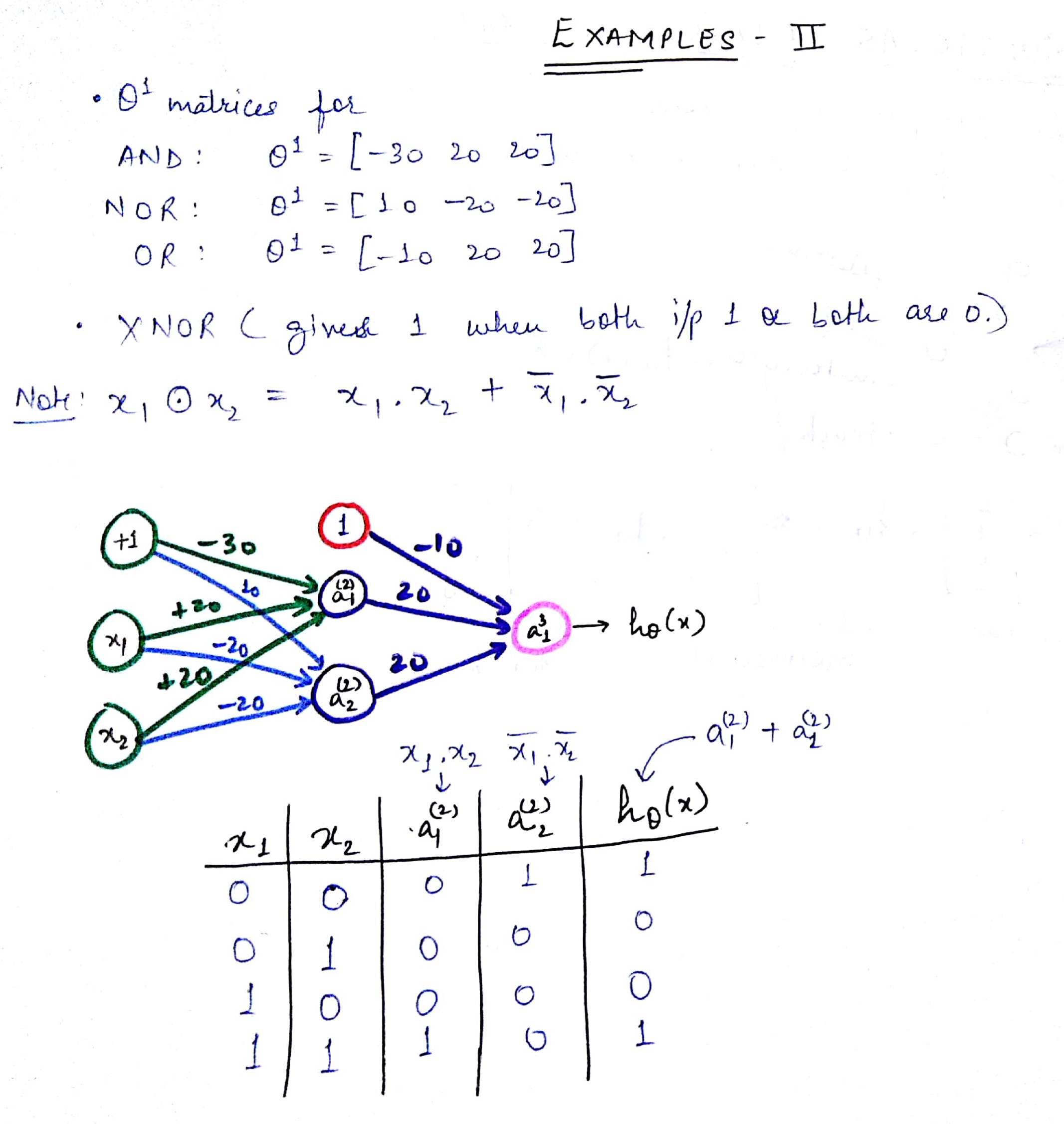
As you can see in the note given in the image that an XNOR boolean operation is made up of AND, OR and NOR boolean operation. The weights have been adjusted for all the three boolean operations.

In the table you can see that the output is 1 only if either both x1 and x2 are 1 or both are 0.

Why are fully connected layers required?

We can divide the whole neural network (for classification) into two parts:

• Feature extraction: In the conventional classification algorithms, like SVMs, we used to extract features from the data to make the classification work. The convolutional layers are serving the same purpose of feature extraction. CNNs capture better representation of data and hence we don’t need to do feature engineering.
• Classification: After feature extraction we need to classify the data into various classes, this can be done using a fully connected (FC) neural network. In place of fully connected layers, we can also use a conventional classifier like SVM. But we generally end up adding FC layers to make the model end-to-end trainable. The fully connected layers learn a (possibly non-linear) function between the high-level features given as an output from the convolutional layers.

Thank You for reading