
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Data compression is the encoding of data in such a way that it takes up less memory space while storing. Huffman coding and Shannon Fano Algorithm are two data encoding algorithms.
Differences between Huffman and Shannon Fano algorithm are as follows:
- Results produced by Huffman encoding are always optimal. Unlike Huffman coding, Shannon Fano sometimes does not achieve the lowest possible expected code word length.
- The Huffman coding uses prefix code conditions while Shannon fano coding uses cumulative distribution function.However Shannon Fano algorithm also produces prefix codes
We will go through the basics of encoding methods and the two algorithms: Huffman coding and Shannon Fano Algorithm so that we can understand the differences better.
There are two types of encoding methods: Fixed length encoding and variable length encoding.
Fixed length encoding
In fixed length encoding, length of code for every character is fixed.
Advantage: Decoding such files is trivial
Disadvantage: This method results in lot of wastage of space.

Variable length encoding
In variable length encoding, codes are of variable length.
Advantage: Space efficient. 25% improvement over fixed length codes. In general, variable length codes can give 20 − 90% space savings.
Disadvantage: Decoding such files are tougher since there are chances of ambiguity.
For example, if 'a' has code 0 and 'b' has code 00. To decode 00, 2 possible cases are possible 'aa' or 'b'.
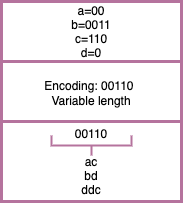
One of the ways to solve this problem is prefix codes, i.e. no codeword is a prefix of another codeword. For example, if the codes are {0,1,11}, this does not satisfy the property of prefix codes since ‘1’ is a prefix of ‘11’.
To decode, find the first valid codeword and keep on repeating the process till the string is decoded.
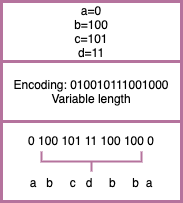
Huffman coding and the Shannon Fano algorithm are two famous methods of variable length encoding for lossless data compression.
Huffman coding
Huffman coding is a very popular algorithm for encoding data. Huffman coding is a greedy algorithm, reducing the average access time of codes as much as possible.
This method generates variable-length bit sequences called codes in such a way that the most frequently occurring character has the shortest code length. This is an optimal way to minimize the average access time of characters. It provides prefix codes and hence ensures lossless data compression and prevents ambiguity.
Understanding the algorithm
- Lets take the example string "aaaa bbb e f iiiiii".
- We start by calculating the frequency of every character in the string (including spaces). Hence frequencies= {'a':4,' ':4,'e':1,'f':1,b:'3'}. Space character is denoted as sp in diagrams.
- Create nodes of all the unique characters and their frequency.
- At every step we select 2 nodes of least frequency and combine them to form node x of frequency equal to sum of selected nodes.
Step 1.

Step 2.
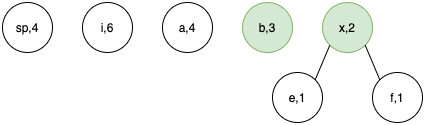
Step 3.
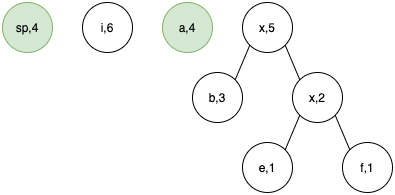
Step 4.
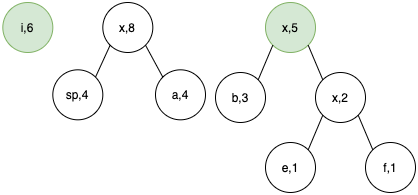
Step 5.
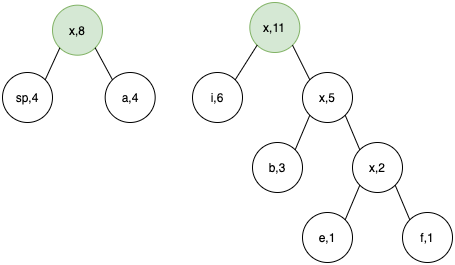
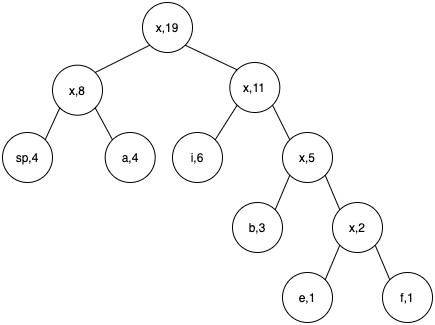
- At this step we have our final tree. Now we have the root node x,19. Now we can traverse the tree to assign codes.
- Start traversing from the root node. Every path to the left of a node is assigned 0 and that to the right is assigned 1.
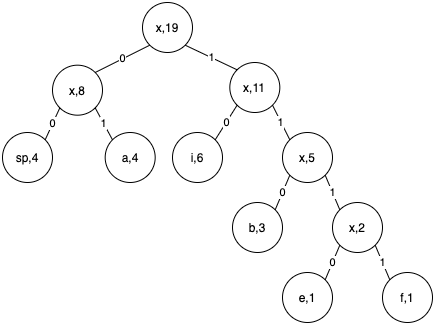
- Now suppose we want to get the codeword corresponding to b. We traverse the tree from root to leaf node b. The code word will be the numbers we encounter on the path.
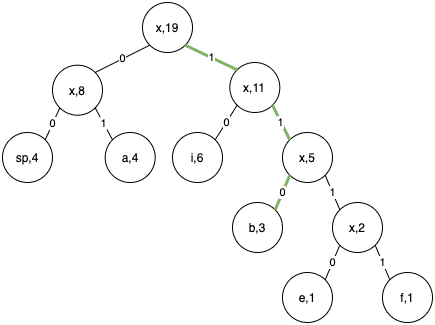
Hence for b, code is 110.
How have we reduced the size?
A character is 1 byte long = 8 bits.
In the given example the string "aaaa bbb e f iiiiii" requires:
8x19 = 152 bits.
Since 0 and 1 take only 1 bit each, with Huffman Encoding the string requires:
Code for a=01=2 bits, b=110 = 3 bits and so on..
Total bits = (freq of 'i')x(length of code for 'i')+ (freq of 'a')x(length of code for 'a')+.....
Total bits = 6x2 + 4x2 + 4x2 + 3x3 + 4x1 + 4x1 = 45 bits only!
Average code length=Total no. of bits/Total no. of symbols = 45/19 = 2.37
i.e. Average code length is 2.37 bits per symbol as compared to 8 bits per symbol before encoding.
Pseudocode
1. Find frequencies of all the characters in the string
2. Make a node corresponding to every (character,frequency)
3. Heapify the nodes
4. While heap has 2 or more nodes
5. Pop 2 nodes say first and second
6. Make a new node x, with frequency = first.freq + second.freq
7. Make first node as left child of x
8. Make second node as right child of x
9. Insert x into the heap
10. Extract the last node which is the root of the tree
/*For assigning codes to each charater,*/
11. Traverse the tree
12. If you move left, assign the path 0
13. If you move right, assign the path 1
14. If you reach the leaf node:
/* Code for the character of the leaf node is the path from the root to that node.*/
Complexity analysis
Given n nodes,
Heapifying n nodes = O(n)
In every iteration we take out 2 nodes and insert 1 node. Therefore for n nodes,it will take n-1 iterations to make the tree
While heap has 2 or more nodes: O(n) (Justified above)
Extract min from heap twice O(logn)
//some constant time operations
Insert x in heap O(logn)
To fetch code for all the nodes, traverse the tree O(n)
Worst case time complexity: Θ(nlogn)
Implementation
Following is the implementation in Python:
class Node:
def __init__(self, val,freq):
self.freq = freq
self.val = val
self.left = None
self.right = None
def __repr__(self):
return ("Node: "+str(self.val)+" Freq: "+str(self.freq))
@property
def __lt__(self, other):
return self.freq < other.freq
def __gt__(self, other):
return self.freq > other.freq
import heapq
def getFrequencies(s):
#store frequencies of every character in the string (including spaces)
d={}
for i in s:
if i in d:
d[i]=d[i]+1
else:
d[i]=1
return d
def convertToNodes(frequencies):
nodeArr=[]
for key in frequencies.keys():
nodeArr.append(Node(key,frequencies[key]))
return nodeArr
def getCodes(root,codeword="",codes={}):
#given the root of a tree, traverses it and returns the code of every character
if root.left==None and root.right==None:
codes[root.val]=codeword
else:
if root.left != None:
getCodes(root.left,codeword+"0",codes)
if root.right != None:
getCodes(root.right,codeword+"1",codes)
return codes
def convertToCode(s,codes):
#takes the string and corresponding code and converts the string to
#encoded form
encodedS=""
for char in s:
encodedS+=codes[char]
return encodedS
def huffmanEncode(heap):
#convert the given nodes into a tree
while(len(heap) < 1):
e1=heapq.heappop(heap)
e2=heapq.heappop(heap)
node=Node("x",e1.freq+e2.freq)
node.left=e1
node.right=e2
heapq.heappush(heap,node)
root=heapq.heappop(heap)
return root #if heap only contains 1 node, that node is root.
#incase you have dict of frequencies, comment code where ever s is used in
#main and make a dict with the variable name frequencies where key is
#character and value is frequency.
s="aaabbccccccddddddddd"
frequencies=getFrequencies(s) #get frequencies of every element
heap=convertToNodes(frequencies) #convert every character into a node
heapq.heapify(heap) #heapify the nodelist
root=huffmanEncode(heap) #encode the string using huffman encoding
codes=getCodes(root)
encodedS=convertToCode(s,codes)
print(codes)
Application of Huffman encoding
- Huffman is widely used in all the mainstream compression formats such as .zip
- Compression to image formats (JPEG and PNG).
- Huffman encoding is also used to compress MP3 files.
- Brotli compression algorithm by Google compresses data using a combination of a modern variant of the LZ77 algorithm, Huffman coding and 2nd order context modeling.
Shannon Fano algorithm
Shannon Fano Algorithm is an entropy coding technique used for lossless data compression. It uses the probabilities of occurrence of a character and assigns a unique variable-length code to each of them.
If c is a character,
Probability(c) = Frequency(c) / sum of frequencies
Understanding the algorithm
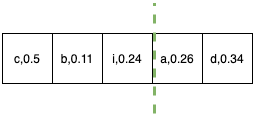
- We start by calculating the probability of occurrence of each character and sort them in increasing order of frequency.
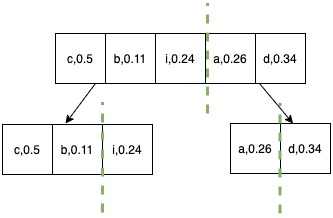
- Divide the characters into two halves(left half and right half) such that the sum of frequencies is as close as possible.
- Repeat the above step for each half until individual elements are left.
Step 1.
Step 2.
Step 3.
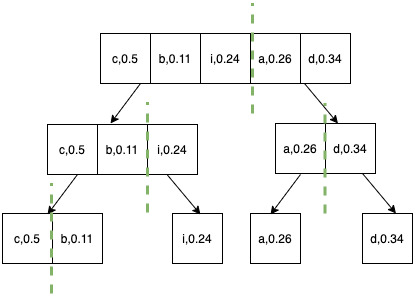
Step 4.

- Append 0 to the codes of the left half and append 1 to the codes of the right half.
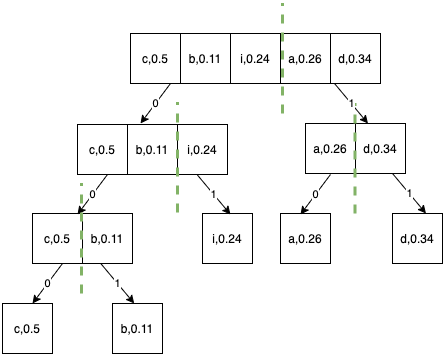
- Final codes are as follows:

Pseudocode
1. Find the probability of occurrence of each character in the string
2. Sort the array of characters in the increasing order of their probabilities, say A
3. fanoShannon(A):
4. If (size(A)==1)
5. return
6. Divide A into left and right such that the difference between the sum of probabilities of left half and right half is minimum
7. Append 0 in the codes of the left half
8. Append 1 in the codes of the right half
9. fanoShannon(left)
10. fanoShannon(right)
Implementation
class Symbol{
char c;
double probability;
String code;
Symbol(char c, Double probability){
this.c=c;
this.probability=probability;
code="";
}
}
static void fanoShannon(ArrayList<Symbol> characters, int beg,int end){
if(beg==end)
return;
int y=beg;
int z=end;
double sum_left=0.0;
double sum_right=0.0;
while(y<=z){
if(sum_left<=sum_right){
sum_left+=characters.get(y).probability;
y++;
}
else{
sum_right+=characters.get(z).probability;
z--;
}
}
for(int h=beg;h<y;h++){
characters.get(h).code+="0";
}
for(int h=y;h<=end;h++){
characters.get(h).code+="1";
}
fanoShannon(characters, beg, y-1);
fanoShannon(characters, y, end);
}
Complexity analysis
The time complexity runs similar to quick sort.
The recurrance relation is the following :
T(n)=T(k)+T(n-k)+Θ(n)
where k and n-k are the size of the partitions, k>0
Worst case:
The partitions done each time can be very unbalanced, for example if the probabilities are {0.05,0.1,0.15,0.2, 0.5}, then the recurrence relation becomes:
T(n)=T(n-1)+T(1)+Θ(n)
T(n) turns out to be Θ(n^2) in this case.
Best case:
If the partitions can be divided in such a way that the sizes are almost equal, for example if the probabilities are {0.2,0.25,0.25,0.3}, then the recurrance relation becomes:
T(n)=2T(n/2)+Θ(n)
T(n) turns out to be Θ(nlogn) in this case.
Question
What is the worst case time complexity of Huffman coding
Question
What are prefix codes?
With this article at OpenGenus, you must have a complete idea of the differences between Huffman coding and Shannon Fano Algorithm. Enjoy.
