Data Encoding is the process of conversion of data in a form suitable for various types of information processing. Encoding is used for data transmissions, data storage, and data compression. It is also used in application processing for file conversions.

Following are the types of data encoding algorithms:

• Lossy encoding
  • Discrete Cosine Transform
  • Fractal Compression
• Lossless encoding
  • Run Length Encoding
  • Lempel-Ziv-Welch Algorithm
  • Huffman coding
  • Fano Shannon encoding
  • Arithmetic coding

We will go through each of the methods in detail now.

Lossy encoding

In the case of lossy encoding, data that is not noticeable is removed. This process reduces the actual data size. However, when decoded, it cannot be restored into its initial state. There is also a loss in the quality of the data since some bits are lost forever.
Lossy encoding generally results in a high degree of compression.
Application: It is used for compressing audios and videos.
Zoom into the following image to notice the difference.

Algorithms for lossy compression

Some of the most famous algorithms for lossy compression are:

1. Discrete Cosine Transform

The data is broken into various frequencies. A large amount of information is stored in a very low-frequency component of a signal. One of the ways to calculate DCT is by using Fourier transformation. Discrete Cosine Transform makes image transmission possible over networks.

2. Fractal Compression

Fractal compression uses the fact that different parts of an image are similar; that is, images can be represented as fractals. Hence storing the image as a collection of transformations could be useful in compressing the data. The algorithm converts these parts into fractal codes, which can then be used to recreate the entire image.
It is hard to determine the compression ratio that can be achieved using Fractal Compression as the image can be decoded at any scale.

Lossless encoding

Lossless encoding keeps the bytes which are non-noticeable while compressing data. Hence, after decoding, the data can be restored to its original state and there is no reduction in quality. Lossless encoding reduces less as compared to lossy encoding, but data can be restored to the original quality.
Application: It is used for compressing text as well as audios and videos. For instance, while creating a zip file.

Algorithms for lossless compression

Some of the most famous algorithms for lossless compression are:

1. Run Length Encoding

Run Length encoding follows a straightforward algorithm, it just picks the next character and appends the character, and it’s count of subsequent occurrences in the encoded string.
For the string “WWWWWWWWWWWWWBBWWBBBBBBBBBBB” , the code is “W13B2W3B11” . The Length reduces from 29 characters to 10 characters. This algorithm can prove highly useful for files with a high number of runs and large run lengths.
However, it will prove to be ineffective for the following cases.
For example,

1. ABCD gets converted to 1A1B1C1D, which takes more space than before.
2. 6666666666655 gets converted to 11625 which can be decompressed to 1-1,62-5, and hence is ambiguous.

2. Lempel-Ziv-Welch Algorithm

LZW algorithm is a very common lossless compression technique. A very significant application of this is Unix's compress command. It is the best dictionary based encoding technique.
This algorithm works by starting with a table of characters numbered from 0 to n-1, n is the number of characters. When encoding begins, strings are identified and numbered from 256 onwards. When a particular substring appears again, it is encoded with the label of the string as a whole instead of a concatenation of codes for individual characters.
For example, the string “ABAB” will be encoded as <0><1><2>, where A has code 0, B has code 1, and AB has code 2.

3. Huffman coding

Huffman coding is another popular algorithm for encoding data. Huffman coding is a greedy algorithm, reducing the average access time of codes as much as possible. It is a tree-based encoding technique.
This method generates variable-length bit sequences called codes in such a way that the most frequently occurring character has the shortest code length. This is an optimal way to minimize the average access time of characters. It provides prefix codes and hence ensures lossless data compression and prevents ambiguity.

4. Fano Shannon encoding

Shannon Fano Algorithm is an entropy coding technique used for lossless data compression. It uses the probabilities of occurrence of a character and assigns a unique variable-length code to each of them.
If c is a character,
Probability(c) = Frequency(c) / sum of frequencies

5. Arithmetic coding

It is an entropy coding technique and can be used for both lossy and lossless compression. It coverts the entire data into one floating-point number between 0 and 1. The interval is further divided into smaller intervals according to the probability/frequency of occurrence of characters.
Arithmetic coding assigns a smaller code to frequently occurring symbols.

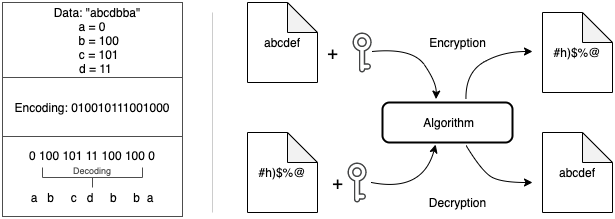
Encoding and Encryption

The idea behind encoding is to convert data in a format such that it is readable by other processes and systems. Encoding is also done to reduce the size of the data and to store it easily. Encoding uses commonly known algorithms and have a standard way of decoding/decompressing.

Encryption, on the other hand, is not decipherable by anyone and everyone. It is done to prevent data theft while transferring sensitive data. Encryption algorithms scramble the data and convert them into cipher text. Data can be decoded only using special keys or algorithms. Common encryption techniques are RSA and AES encryption.

With this article at OpenGenus, you must have a good understanding of different data encoding algorithms. Enjoy.