In this article, we have explored in great detail some of the different factorization algorithms for Integers such as Trial Division, Pollard's rho algorithm, Dixon's algorithm and Quadratic Sieve.

Table of Contents

• Introduction
• Category 1 algorithms
  • Trial division
  • Pollard's rho algorithm
• Category 2 algorithms
  • Dixon's algorithm
  • Quadratic sieve

The Time Complexity of the different algorithms for Integer Factorization are:

Algorithm	Time Complexity
Trial division	O(N)
Pollard's rho algorithm	O(N1/2)
Dixon's algorithm	O(e2√2 √(logn loglogn))
Quadratic sieve	O(e(√(log n log log n)))

Let us get started with Integer Factorization Algorithms.

Introduction

In number theory, integer factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equals the original integer. There are many different algorithms present to factorize an integer. Depending on the running time of the algorithms, they have been classified into Category 1 and Category 2 which comprises of non-quantum integer factorization algorithms.

Category 1 algorithms

This category of algorithms are also known as special purpose algorithms. The running time of these algorithms depend on certain parameters or unknown factors of the integers like the size, special form, etc.

Some algorithms that come under this category are:

• Trial division
• Pollard's rho algorithm

Let us discuss these algorithms in detail.

Trial division

In trial division, the integer to be factorized (n) is divided by every number less than it. It consists of continually testing if n is divisible by a smaller number.
Further research has shown that the factors of n may be less than or equal to half of it (n/2), but never greater. Implementing this improves the efficiency of this algorithm.Given below is the code for the above

def trial_division(n: int) :
    a = []              
    f = 2                  
    while n > 1:        
        if n % f == 0:          
            a.append(f)  
            n //= f       
        else:            
            f += 1       
    return a 
trial_division(12)

The above program gives a list of prime factors of 12 using the trial division.

Output:

[2,2,3]

The Time Complexity of the above algorithm is O(N). Specifically, there are N/2 steps.

Pollard's rho algorithm

In this algorithm, the greatest common divisor of modulus of the difference between two integers and the integer to be factorized (n) is found out. If it is greater than 1, then that is one of the non-trivial factors of n.

This algorithm gets its name 'rho' as the sequence generated will cycle as each value depends on the value before it and the structure of this cycling resembles the Greek letter rho.

The two integers are found by using a function   f which generates pseudo random numbers. One such function used is  f = x²+ a mod n where a is generated using a random number generator. We generally start with x₁=2 and perform the operations x₂=f(x₁), x₃=f(x₂) i.e. the general rule is x_n+1=f(x_n).

Scheme for the algorithm

x = 2;

while (.. exit criterion .. )

   y = f(x);
   p = GCD( | y - x | , N);
   if ( p > 1)
       return "Found factor:";
   x = y;
end

return "Failed"

Example:

Let us take n = 55 and f(x) = x² + 2 mod 55.In the table below GCD refers to GCD(|x_n - x_(n+1)|, N).

xn	x(n+1)	GCD
2	6	1
6	38	1
38	16	1
16	36	5

From the table, 5 is one of the non-trivial factors of 55. The other factor can simply be found by dividing 55 by 5 or continuing the algorithm. Therefore, the factors are 5 * 11.

The Time Complexity of this algorithm will be O(N^1/2) where N is the total number of possible values.

Category 2 algorithms

This category of algorithms are also known as general purpose algorithms or Kraitchik family algorithms. The running time of these algorithms depend on only on the size of the integer to be factored. They are used to factor RSA numbers.

Some algorithms that come under this category are:

• Dixon's algorithm
• Quadratic sieve

Let us explore these algorithm in depth.

Dixon's algorithm

Let the number to be factorized be n.

• We choose a bound b and a factor base (p) of all primes less than or equal to b.

• Look for an integer x such that   x² mod(n) is b-smooth.
  

( An integer greater than 0 is called b-smooth if all of its prime factors are lesser than or equal to b).

• After we obtain sufficient realtions, we use methods like Gaussian elimination to multiply them together and obtain a final expression in the form  y²= z² mod(n) .

• We then find the factors of the above equation as

GCD(y - z, n), GCD(y + z, n).

The Time Complexity of this method is O(e^{2√2 √(logn loglogn)}) where e = 2.718.

Example

Say we want to factor n = 23449 over p = 2, 3, 5, 7 and b=7.
x = [√n] = 154. Starting here, the first related squares we get are:

970² mod(23449) = 2940 = 2² ∗ 3 ∗ 5 ∗ 7²
8621² mod(23449) = 11760 = 2⁴ ∗ 3 ∗ 5 ∗ 7²

Here, 970 and 8621 are b-smooth numbers whose factors are not greater than 7.

So, (970* 8621)² ≡ (2³ ∗ 3 ∗ 5 ∗ 7²)² (mod 23449)

That is, 14526² ≡ 5880² (mod 23449)

Now , we find:

gcd(14526-5880,23449) = 131
gcd(14526+5880,23449) = 179
Factors are N = 131 * 179

Quadratic sieve

This algorithm is a modification of Dixon's algorithm.

In Dixon's algorithm, we chose 2 from the set of realtios obtained to arrive at the 'congruence of squares modulo n' form. But here, we assign a variable to each of the relation, and work mod 2 so that all the exponents are even. We then obtain a set of reduced relations and then find the values of the variables. These values will tell us which realtions are to be considered so that we get a 'congruence of squares modulo n' form.

The theoretical time and space complexity of this algorithm is O(e^{(√(log n log log n))}).

Example

Let the number to be factorized be n = 539873 and b=19
x = [√n] = 734.6. Starting from 735, we work our way up.

Working mod 539873:
735² ≡ 352 ≡ 2⁵ ∗ 11
750² ≡ 22627 ≡ 11³ ∗ 17
783² ≡ 73216 ≡ 2⁹ ∗ 11 ∗ 13
801² ≡ 101728 ≡ 2⁵ ∗ 11 ∗ 17²

Solving

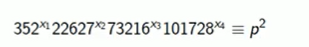
we get,

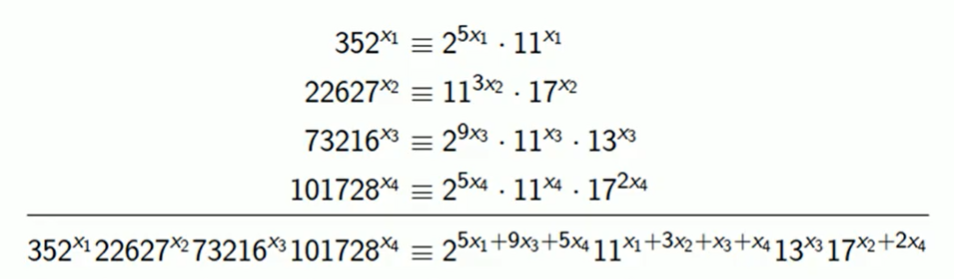
working mod 2:

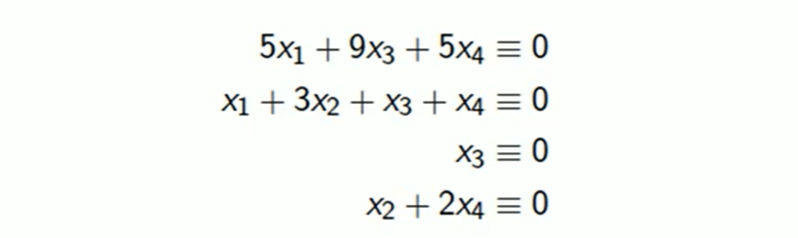
which gives us a non trivial solution x₁=1, x₂=0, x₃=0, x₄=1.

Therefore, the first and fourth relations are multiplied to get the 'congruence of squares modulo n' form.

Further proceeding, we have:

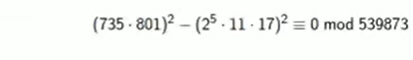
By applying the congruence of squares, we will find that the GCD of the difference of the two integers and 539873 will be a factor of 539873. That is:

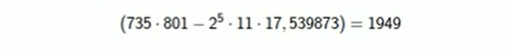
Hence, 539873 = 1949 * 277

With this article at OpenGenus, you must have the complete idea of Integer Factorization Algorithms.