In this article, we are going to explore an algorithm to interleave first half of queue with second half.

Contents

1. Introduction to the problem
2. Example Input and Output
3. Approach to Solve the Problem
4. Steps Recap
5. Code Implementation.
6. Output
7. Time Complexity
8. Space Complexity

Pre-requisites:

• Queue data structure
• Reverse a Queue using another Queue

Introduction to the problem

We are provided with a queue of integers.If it is of even length,then we have to rearrange the elements by interleaving the first half of the queue with second half of the queue.

For auxillary space, we are using stack only.

Example Input and Output

input: 3 4 5 2
output:3 5 4 2

input: 76 4 56 2 7 1
output:76 2 4 7 56 1

Approach to Solve the Problem

Let us look at the problem with the help of an example.

We are refering to the queue 5 6 2 4

We know the answer should be 5 2 6 4

Let us consider the auxillary space available that is the stack.

We are pushing the first half of the elements in the queue to the stack.

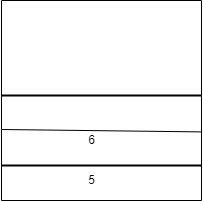
But we need the elements in the stack in reverse order so that we can take one element from the stack and one from the queue and thus print alternatively.

Now we pop the elements from the stack back to the end of queue.

The queue will look like this.

Now we will dequeue the first half of the elements from the queue and add it to the end of the queue so that the popped elements from the stack comes first in the queue.

The queue is now:

We will then take and put the now first half of elements to the stack.

The stack will be:

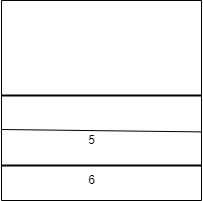
The resulting queue is:

Now we will be arranging the numbers in interleaved fashion.

Take 2 pointers,one pointing to the queue and other the top of stack.

Pop top element of stack and add it to the end of queue.(that is pop 6 from stack and add it to the end of queue).The first element of the queue is moved to the end of the queue.(move 2 to the end of queue)Update the pointers.

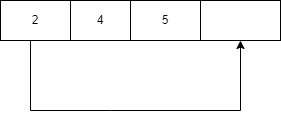
Now pop the next element that is 6 from stack and push it to the queue.The now first element (i.e,4) is pushed to the end of queue.

The final queue is:

Which is what we needed.It contains the numbers from first half of queue and second half of queue in interleaved fashion.

Steps Recap

1. Push first n/2 element from queue to stack
2. Pop elements from stack and add to queue.
3. Move first n/2 elements of queue to end of queue.
4. Push first n/2 elements to stack.
5. Write to the queue the elements in the stack and queue in interleaved fashion.

Code Implementation

Following to the implementation in C++ to interleave first half of Queue with second half of Queue:

#include <bits/stdc++.h>
using namespace std;

void intLeaveQue(queue<int>& q)
{
	
	if (q.size() % 2 != 0)
		cout << "You have entered odd number of elements!." << endl;

	stack<int> s;
	int halfSize = q.size() / 2;

	for (int i = 0; i < halfSize; i++) {
		s.push(q.front());
		q.pop();
	}

	while (!s.empty()) {
		q.push(s.top());
		s.pop();
	}

	for (int i = 0; i < halfSize; i++) {
		q.push(q.front());
		q.pop();
	}

	for (int i = 0; i < halfSize; i++) {
		s.push(q.front());
		q.pop();
	}

	while (!s.empty()) {
		q.push(s.top());
		s.pop();
		q.push(q.front());
		q.pop();
	}
}

int main()
{
	queue<int> q;
	q.push(5);
	q.push(6);
	q.push(2);
	q.push(4);
	
	intLeaveQue(q);
	int length = q.size();
	for (int i = 0; i < length; i++) {
		cout << q.front() << " ";
		q.pop();
	}
}

Output

5 2 6 4 

...Program finished with exit code 0
Press ENTER to exit console.

Time Complexity

As the loop is iterating to N/2 and the loop is present 5 times.Therefore the time complexity is O(N).

Space Complexity

As we have used an extra stack, the extra space or auxillary space required is O(n).

Thus with this article at OpenGenus, we have learned how to implement interleaving first half of queue with second half.