MiniMax Algorithm: How Machine thinks?

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

Reading time: 30 minutes | Coding time: 20 minutes

Have you ever wondered how computers make its move in chess, tic-tac-toe, or any other multiplayer strategic board game? Well! That's what we are going to look into this lesson precisely. This article will focus on the most popular decision-making strategy algorithms appointed by programmers in various strategic games. The name of the algorithms is the Minimax Algorithm, which is one of the many game theory algorithms in computer science.

Before moving further, I want you to think about the situation in which you are playing a tic-tac-toe game, and it's your turn to make a move, so how you think at that time? Generally, a sensible being will think, " If I make this move am I in winning or losing position? " This is what this algorithm does to make decisions accurately.

Let's dive into a naive overview of the algorithm. You can consider the decision-making structure as a tree where the root node is the initial configuration of the board, and its children are all possible moves. You might start getting intuition in your mind about the working of the algorithm. In the tree, every alternate level is the moves made by the computer, and other levels are the moves that can be made by the user.

So what computer does is that whenever a computer requires to make a move, it traverses through all the possible steps assuming that the user plays optimally. Then out of all the possible outcomes, it chooses the one with the maximum probability of winning. We will see the detailed explanation as we move forward.

So here is the definition of the Minimax algorithm:
Minimax is a recursive algorithm used to choose an optimal move for a player, assuming that the opponent is also playing optimally. As its name suggests, its goal is to minimize the maximum loss (reduce the worst-case scenario).

Here are the few steps that the computer follows at each move:

Return the desired value if the final state (leaf node) reaches. For Eg: The programmer can set +5 for winning, 0 for a tie, and -5 for losing state.
If it is not the final state, then go through all the possible positions on board.
For each location, call the Minimax algorithm.
Analyze the returning values and make the best move accordingly.

The algorithm traverses the whole tree in the DFS manner. If you are not familiar with the DFS, then I would recommend you to checkout the article on DFS in the tree by Alexa Ryder.

Before implementing the code we need to look at the two most important aspects of this algorithm.

Minimum Value

Minimizer is the first part of the algorithm, and it tells us that from the given set of positions, which one offers the minimum result or losing state. You might be thinking that we should look for the winning state, but we have to predict the opponent's move in advance. As we already know that the algorithm assumes that the user plays optimally, so by this minimizing function computer already knows the opponent's next move. That's why we need the losing state from the set of positions.

Maximum Value

You might have already guessed the function of this algorithm. That's right, it is exact opposite of the Minimizer and from the given set of positions it chooses one with maximum value.
Hence the name of our algorithm is the Minimax Algorithm. Now enough of boring theory, let's visualize the stuff to get a better understanding of the algorithm.

Pseudo Code and Visualization

Before diving into the coding part, let's quickly go through our pseudo code. I will explain it step by step by taking our all time favourite tic-tac-toe board game as example.

PseudoCode for minimax():

First check whether we already have winner.
If not then check for final state of board.
If neither of the above case then see if it would be user turn or cpu turn.
Accordingly take minimum or maximum of the values returned from further recursive calls.
At last update the "pos" variable everytime maximum or minimum is found.

PseudoCode for main():

Initialize array of size 9.
Alternately take input from user.
After each user input, Call minimax() to get optimal position.
Print CPU moves.
At the end print the winner.

Here is the explanation with tic-tac-toe as an example:

We will first declare an array of size 9 to simulate the tic-tac-toe board.
We will initilize each element of an array with 2, here 2 represents that the box is not filled yet.
I will explain this from intermediate state of board as shown below:

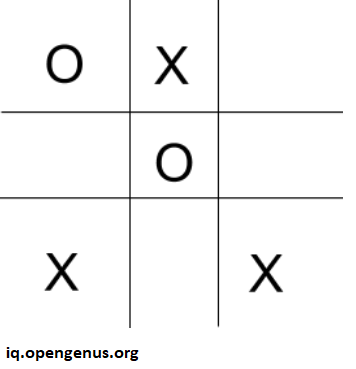
board_state-1

Content of our array would be [0,1,2,2,0,2,1,2,1], where 1 signifies that box is filled by user and 2 signifies that box is filled by the computer.
Now it's computer's turn to make a move. We will make a call to our Minimax algorithms which will return the optimal position where to place the 0.
Here's the recursion tree which shows how DFS will generate all the cases and return the best possible move.

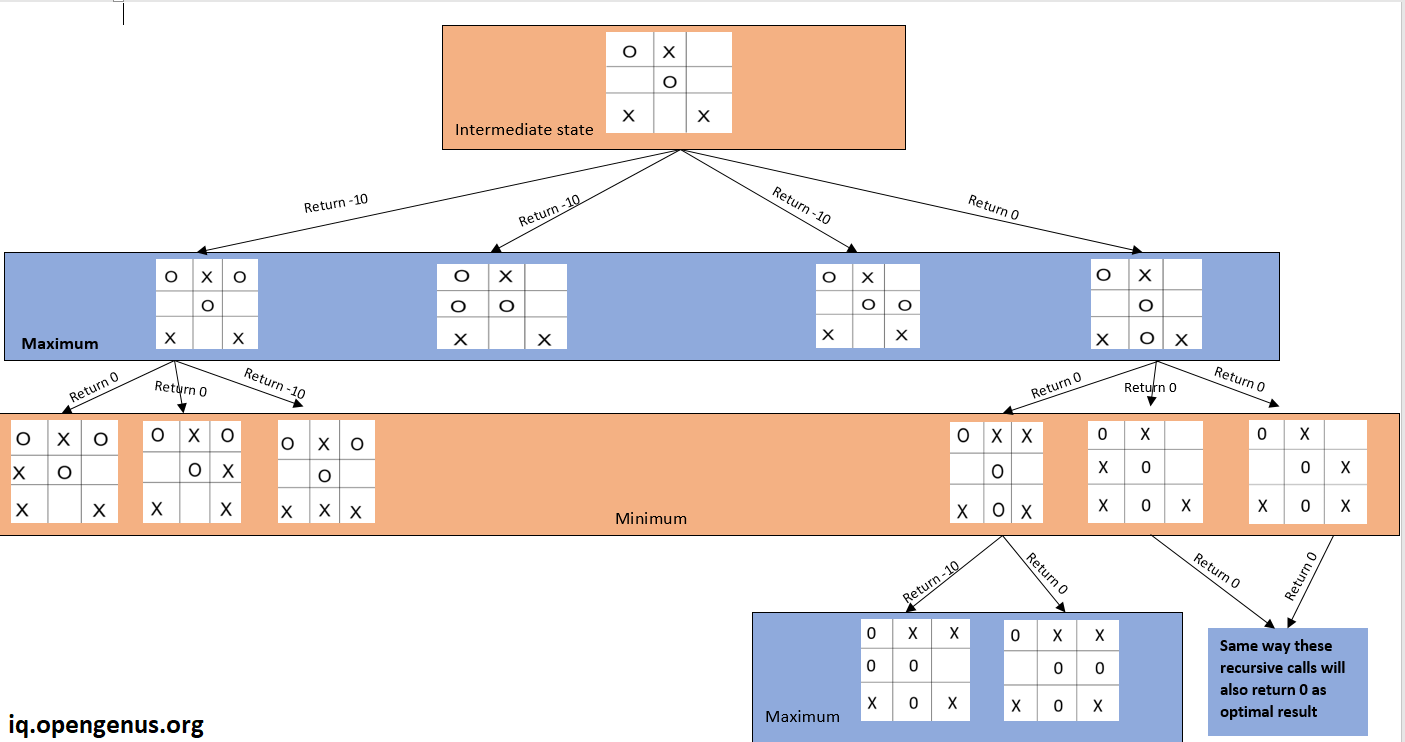
recursion_tree-1

As We can see that from this intermediate state, our algorithm will go through each empty slot and get result from there and chooses the path which returns the maximum result i.e last call where we place 'O' between two 'X'
Each recursive call perform dfs on subtree and return the optimal result and we take maximum or minimum according to whose turn it is.

I hope now algorithm has fit clearly in your mind. If not, my suggestion is to take a notebook and dry run the algorithm to get crystal clear clarity as clarity is very important to understand the code implementation.

If you are confident with this algorithm, then I will recommend you to write your own code to implement this algorithm before seeing the solution.

Coding

Now let's get our hands dirty with the coding stuff. Before we start looking the code these are the some exception that I have assumed while writing this code:

User will not input the already entered box.
Basic knowledge of recursion is required to analyze the code.
Mind should be fresh as thing will start getting bit complicated.

 #include <bits/stdc++.h>
 using namespace std;
 
 bool isFinalState(vector<int> &board_state){
     for(int i:board_state){
         if(i!=0&&i!=1){
             return false;
         }
     }
     return true;
 }
 
 int is_any_winner(vector<int> &board_state){
     if((board_state[0]==board_state[1])&&(board_state[1]==board_state[2])&&board_state[0]!=2)
         return board_state[0];
     else if((board_state[3]==board_state[4])&&(board_state[4]==board_state[5])&&board_state[3]!=2)
         return board_state[3];
     else if((board_state[6]==board_state[7])&&(board_state[7]==board_state[8])&&board_state[6]!=2)
         return board_state[6];
     else if((board_state[0]==board_state[4])&&(board_state[4]==board_state[8])&&board_state[0]!=2)
         return board_state[0];
     else if((board_state[2]==board_state[4])&&(board_state[4]==board_state[6])&&board_state[2]!=2)
         return board_state[2];
     else if((board_state[0]==board_state[3])&&(board_state[3]==board_state[6])&&board_state[0]!=2)
         return board_state[0];
     else if((board_state[1]==board_state[4])&&(board_state[4]==board_state[7])&&board_state[1]!=2)
         return board_state[1];
     else if((board_state[2]==board_state[5])&&(board_state[5]==board_state[8])&&board_state[2]!=2)
         return board_state[2];
     else return -1;
 }
 
 int minimax(int turn,vector<int> &board_state,int &pos){
     int any_winner = is_any_winner(board_state);
     if(any_winner!=-1){
         if(any_winner==0)
             return 10;
         else return -10;
     }
     else if(isFinalState(board_state)){
         return 0;
     }
     else {
 
         int value;
         if (turn == 0)
             value = -10;
         else value = 20;
         for (int i = 0; i < 9; ++i) {
             if (board_state[i] != 0 && board_state[i] != 1) {
                 board_state[i] = turn;
                 if (turn == 0) {
                     int pos_ = 2;
                     int temp = minimax(1, board_state, pos_);
                     if (temp > value) {
                         value = temp;
                         pos = i;
                     }
                 } else {
                     int pos_ = 2;
                     int temp = minimax(0, board_state, pos_);
                     if (temp < value) {
                         value = temp;
                         pos = i;
                     }
                 }
                 board_state[i] = 2;
             }
         }
         return value;
     }
 }
 
 int main(){
     vector<int> board_state(9,2);
     int turn = 1;
     while(true){
         if(turn){
             cout<<"User's move: ";
             int pos;
             cin>>pos;
             board_state[pos] = 1;
             turn  = 0;
         }
         else{
 
             int pos = 2;
             minimax(0,board_state,pos);
             board_state[pos] = 0;
             int win = is_any_winner(board_state);
             if(win!=-1){
                 cout<<((win==0)?"CPU":"USER")<<" Wins!";
                 return 0;
             }
             else{
                 if(isFinalState(board_state)){
                     cout<<"Tied!";
                     return 0;
                 }
                 cout<<"Opponent's move: "<<pos<<"\n";
                 turn = 1;
                 continue;
             }
         }
     }
 }

Now here we begin explanation of this code and most of it is according to the pseudocode :

IsFinalState()

At the top, We have function isFinalState(), which return true when we reached the terminal state of the board. It basically traverse the array and check that all the slots are filled either by user or CPU.

is_any_winner()

Next, We have is_any_winner() function which returns 0 if CPU is winner, it returns 1 if user is winner, otherwise it returns -1.
is_any_winner() checks all the 8 cases of matching in tic-tac-toe. These are three horizontal rows, three vertical columns and two main diagonals.

minimax()

And now we have our minimax() function implemented.
Fistly we checks the winner and returns the value accordingly if there is any winner.
If we don't have winner then we check whether the final state is reached. If true then, it is the case of tie.
If neither of above two cases then we initialize our variable value with -10 if it's CPU's turn otherwise 20.
As we need maximum value in case of CPU's turn and minimum value in case of user's turn. As user always tries to minimize our value with his move.
For loop in minimax() goes through all the nine slots of board.
If condition becomes true that whether it's empty slot then we try to make decision that if this was my move or opponent's move. What would be the returning value.
Returning value is stored in temp variable.
Then if it is CPU's turn, we will maximize our value and store our position in "pos" variable.
But if it is user's turn, we will minimize our value and make further predictions according to this minimum value.

main()

Now we move to the main() function, I have taken vector of size 9 and initialized all postions with 2
Then there is while loop which alternately take input from user.
After each user's turn, we call our minimax() to decide our computer's move.
Then we check for the winner and print message accordingly.

Great! You made it to the end of the article. I hope you find this article very informative. If you have any queries regarding this algorithm, let me know in the comments. I will be happy to help you. So that's all for this article and stay tuned for further posts. In meanwhile, check out other excellent posts on https://iq.opengenus.org/

MiniMax Algorithm: How Machine thinks?

Algorithms Software Engineering

Minimum Value

Maximum Value