
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 20 minutes
Autoencoder is a neural network tries to learn a particular feature of converting an input to an output data and generate back the input given the output. It includes two parts:
- encoder: which learns the features of the data or given answers
- decoder: which tries to generate the answers from the learnt features/ questions
This technique is widely used for a variety of situations such as generating new images, removing noise from images and many others.
Read about various applications of AutoencodersIn this article, we will learn how autoencoders can be used to generate the popular MNIST dataset and we can use the result to enhance the original dataset. We will build an autoencoder from scratch in TensorFlow and generate the actual images from the MNIST dataset.
Idea of using an Autoencoder
The basic idea of using Autoencoders for generating MNIST digits is as follows:
-
Encoder part of autoencoder will learn the features of MNIST digits by analyzing the actual dataset. For example, X is the actual MNIST digit and Y are the features of the digit. Our encoder part is a function F such that F(X) = Y.
-
Decoder part of autoencoder will try to reverse process by generating the actual MNIST digits from the features. At this point, we have Y in F(X)=Y and try to generate the input X for which we will get the output.
The idea of doing this is to generate more handwritten digits dataset which we can use for a variety of situations like:
- Train a model better by covering a larger possibility of handwritten digits
As there will be multiple features of handwritten digits, until our autoencoder is over trained, we will generate a different set of handwritten digits than MNIST which is expected to differ by a small amount and will be beneficial in expanding the dataset.
Building our Autoencoder
We use use TensorFlow's Python API to accomplish this.
Import all the libraries that we will need, namely tensorflow, keras, matplotlib, .
import tensorflow as tf
from tensorflow import keras
import matplotlib.pyplot as plt
Define constant parameter for batch size (number of images we will process at a time).
batch_size = 128
Fetch the data from MNIST dataset and load it. Note we take the MNIST dataset to learn the features which we will use to regenerate the dataset.
digits_mnist = keras.datasets.mnist
(train_images, train_labels),(test_images, test_labels) = digits_mnist.load_data()
Create local dataset using tensorflow. Train the data and split it into batches in accordance with the batch size. Reshape each of the image data to equivalent size.
with tf.variable_scope("DataPipe"):
dataset = tf.data.Dataset.from_tensor_slices(train_images)
dataset = dataset.map(lambda x: tf.image.convert_image_dtype([x], dtype=tf.float32))
dataset = dataset.batch(batch_size=batch_size).prefetch(batch_size)
iterator = dataset.make_initializable_iterator()
input_batch = iterator.get_next()
input_batch = tf.reshape(input_batch, shape=[-1, 28, 28, 1])
Iterate through the batches till none are left
init_vars = [tf.local_variables_initializer(),tf.global_variables_initializer()]
with tf.Session() as sess:
sess.run([init_vars, iterator.initializer])
while 1:
try:
batch = sess.run(input_batch)
print(batch.shape) # Get batch dimensions
plt.imshow(batch[0,:,:,0] , cmap='gray')
plt.show()
except tf.errors.OutOfRangeError:
print('All batches have been iterated!')
break
Encoding phase
This is the encoding function. Use convolutional layers along with padding to help maintain the spatial relations between pixels. Compute the mean, standard deviation and epsilon value. Calculate the value z using the first 3 values mentioned.
def encoder(X):
activation = tf.nn.relu
with tf.variable_scope("Encoder"):
x = tf.layers.conv2d(X, filters=64, kernel_size=4, strides=2, padding='same', activation=activation)
x = tf.layers.conv2d(x, filters=64, kernel_size=4, strides=2, padding='same', activation=activation)
x = tf.layers.conv2d(x, filters=64, kernel_size=4, strides=1, padding='same', activation=activation)
x = tf.layers.flatten(x)
mean_ = tf.layers.dense(x, units=FLAGS.latent_dim, name='mean')
std_dev = tf.nn.softplus(tf.layers.dense(x, units=FLAGS.latent_dim), name='std_dev') # softplus to force >0
epsilon = tf.random_normal(tf.stack([tf.shape(x)[0], FLAGS.latent_dim]), name='epsilon')
z = mean_ + tf.multiply(epsilon, std_dev)
return z, mean_, std_dev
Note: Z captures the features of the MNIST dataset
Decoding phase
This is the decoding function. Here, we transpose the convulations. But before that apply some non linear transformations using dense layers. To recover the original image, use the unsampling method from the latent variables.
def decoder(z):
activation = tf.nn.relu
with tf.variable_scope("Decoder"):
x = tf.layers.dense(z, units=FLAGS.inputs_decoder, activation=activation)
x = tf.layers.dense(x, units=FLAGS.inputs_decoder, activation=activation)
recovered_size = int(np.sqrt(FLAGS.inputs_decoder))
x = tf.reshape(x, [-1, recovered_size, recovered_size, 1])
x = tf.layers.conv2d_transpose(x, filters=64, kernel_size=4, strides=1, padding='same', activation=activation)
x = tf.layers.conv2d_transpose(x, filters=64, kernel_size=4, strides=1, padding='same', activation=activation)
x = tf.layers.conv2d_transpose(x, filters=64, kernel_size=4, strides=1, padding='same', activation=activation)
x = tf.contrib.layers.flatten(x)
x = tf.layers.dense(x, units=28 * 28, activation=None)
x = tf.layers.dense(x, units=28 * 28, activation=tf.nn.sigmoid)
img = tf.reshape(x, shape=[-1, 28, 28, 1])
return img
Running the encoding and decoding phase
Link the encoder and decoder.
z, mean_, std_dev = encoder(input_batch)
output = decoder(z)
Reshape input and output to flat vectors.
flat_output = tf.reshape(output, [-1, 28 * 28])
flat_input = tf.reshape(input_batch, [-1, 28 * 28])
Compute the loss function using the binary cross entropy formula. Then calculate the latent loss using the KL divergence formula and finally get the mean of all the image losses.
with tf.name_scope('loss'):
img_loss = tf.reduce_sum(flat_input * -tf.log(flat_output) + (1 - flat_input) * -tf.log(1 - flat_output), 1)
latent_loss = 0.5 * tf.reduce_sum(tf.square(mean_) + tf.square(std_dev) - tf.log(tf.square(std_dev)) - 1, 1)
loss = tf.reduce_mean(img_loss + latent_loss)
Train the model
This is the training loop. For each sample, we create an artificial image and display it. Latent space plot is also being created here
while True:
try:
sess.run(optimizer)
if flag:
summ, target, output_ = sess.run([merged_summary_op, input_batch, output])
f, axarr = plt.subplots(FLAGS.test_image_number, 2)
for j in range(FLAGS.test_image_number):
for pos, im in enumerate([target, output_]):
axarr[j, pos].imshow(im[j].reshape((28, 28)), cmap='gray')
axarr[j, pos].axis('off')
plt.savefig(os.path.join(results_folder, 'Train/Epoch_{}').format(epoch))
plt.close(f)
flag = False
writer.add_summary(summ, epoch)
artificial_image = sess.run(output, feed_dict={z: np.random.normal(0, 1, (1, FLAGS.latent_dim))})
plt.figure()
with sns.axes_style("white"):
plt.imshow(artificial_image[0].reshape((28, 28)), cmap='gray')
plt.savefig(os.path.join(results_folder, 'Test/{}'.format(epoch)))
plt.close()
if FLAGS.latent_dim == 2 and FLAGS.plot_latent:
coords = sess.run(z, feed_dict={input_batch: test_images[..., np.newaxis]/255.})
colormap = ListedColormap(sns.color_palette(sns.hls_palette(10, l=.45 , s=.8)).as_hex())
plt.scatter(coords[:, 0], coords[:, 1], c=test_labels, cmap=colormap)
cbar = plt.colorbar()
if FLAGS.dataset == 'digits-mnist':
cbar.ax.set_yticklabels(['one', 'two', 'three', 'four', 'five', 'six', 'seven', 'eight', 'nine'])
plt.title('Latent space')
plt.savefig(os.path.join(results_folder, 'Test/Latent_{}'.format(epoch)))
plt.close()
except tf.errors.OutOfRangeError:
break
This is the plot of the latent space:
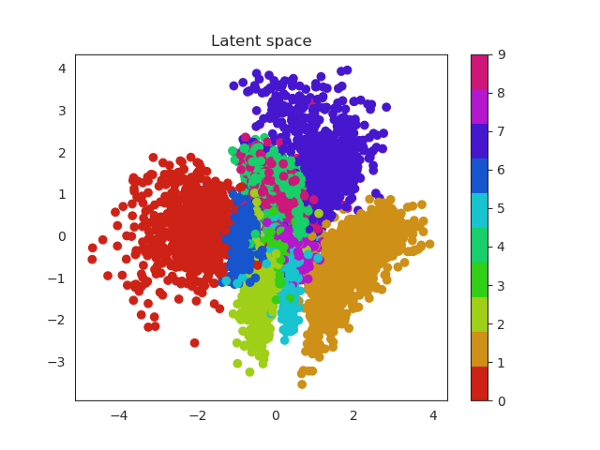
Latent space is the output of the encoder phase which the decoder phase will use. Each point represents a feature or an input MNIST digit and the clusters represent that the points belong to a single digits.
The decoder phase uses this representation to regenerate the MNIST dataset.
Create a mesh grid of values. The matrix that will contain the grid of images.
values = np.arange(-3, 4, .5)
xx, yy = np.meshgrid(values, values)
input_holder = np.zeros((1, 2))
container = np.zeros((28 * len(values), 28 * len(values)))
Run the test images in the matrix which generates the output.
for row in range(xx.shape[0]):
for col in range(xx.shape[1]):
input_holder[0, :] = [xx[row, col], yy[row, col]]
artificial_image = sess.run(output, feed_dict={z: input_holder})
container[row * 28: (row + 1) * 28, col * 28: (col + 1) * 28] = np.squeeze(artificial_image)
plt.imshow(container, cmap='gray')
plt.savefig(os.path.join(results_folder, 'Test/Space_{}'.format(epoch)))
plt.close()
Output
The top line is the input and bottom line is the output-
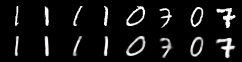
The output image may seem to be similar to the input image but there are small differences which can be measured using a similarity metric.
Enjoy the autoencoder model
