
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will develop a multithreaded java program to find all prime numbers below than N. We will use Sieve of Eratosthenes algorithm to find prime numbers and it will be run in parallel.
Introduction
- Prime numbers are an important and fundamental concept in mathematics, and finding all prime numbers less than a given limit is a common problem in computer science.
- The Sieve of Eratosthenes algorithm is a popular and efficient way to solve this problem, but it is inherently sequential and can be slow for large values of N.
- However, by dividing the range of numbers into several blocks and assigning each block to a separate thread, it is possible to parallelize the algorithm and obtain significant speedup.
- In this article, we will explore how to write a multi-threaded Java program to find all prime numbers less than a given number N using the Sieve of Eratosthenes algorithm.
- We will also discuss some of the challenges and tradeoffs involved in parallelizing the algorithm, and provide a sample implementation in Java.
Sieve of Erastosthenes
- In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit.
- The Sieve of Eratosthenes algorithm is a simple and efficient way to find all prime numbers up to a given limit.
- It works by creating a boolean array of size N, where each entry represents whether the corresponding number is prime or composite.
- Initially, all entries are set to true, but as the algorithm progresses, composite numbers are marked as false.
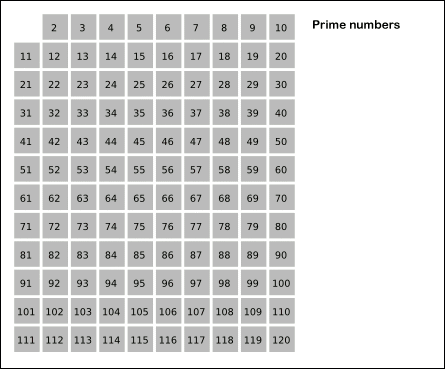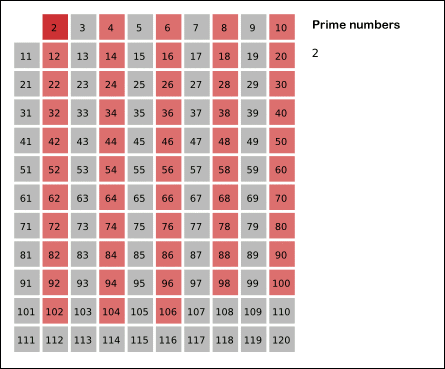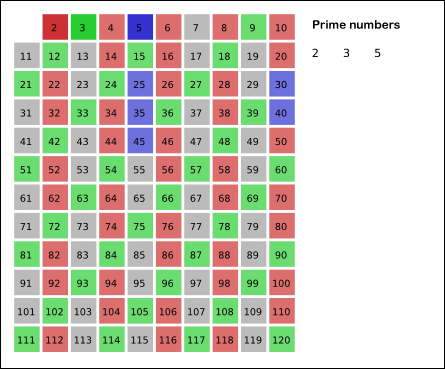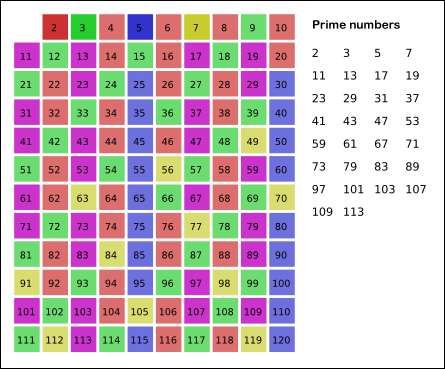
- The algorithm starts with the number 2, which is the first prime number, and then iteratively marks all multiples of 2 as composite, then all multiples of 3, and so on, until only the prime numbers remain.
Approach
The approach of program for Multi-threaded Java program to find all prime numbers less than a given number N using the Sieve of Eratosthenes algorithm is as follows:
-
Divide the range of numbers into blocks: In order to parallelize the Sieve of Eratosthenes algorithm, we need to divide the range of numbers (from 2 to N) into several blocks, where each block contains a subset of the numbers. The number of blocks will depend on the number of available threads.
-
Assign each block to a separate thread: Once the range of numbers has been divided into blocks, we can assign each block to a separate thread. The threads will work in parallel to compute the prime numbers in their respective blocks.
-
Mark the multiples of primes in each block: Each thread will use the Sieve of Eratosthenes algorithm to mark the multiples of the primes in their block. To do this, each thread will start with the first prime number in its block, and mark all of its multiples. It will then move on to the next unmarked number, which will be the next prime in the block, and repeat the process until all primes in the block have been processed.
-
Merge the results: Once each thread has finished processing its block, the results can be merged to obtain the final list of prime numbers. This can be done by concatenating the lists of prime numbers from each block in the order in which they appear.
-
Handle edge cases: There are a few edge cases that need to be handled when parallelizing the Sieve of Eratosthenes algorithm. For example, the first few primes (2, 3, 5, and 7) are not multiples of any other prime, so they need to be handled separately. Additionally, the number of blocks should be chosen to balance the workload among the threads, and there may be cases where the range of numbers is too small to make parallelization worthwhile.
By following this approach, we can write an efficient multi-threaded Java program to find all prime numbers less than a given number N using the Sieve of Eratosthenes algorithm.
Implementation
import java.util.ArrayList;
import java.util.List;
public class ParallelPrimeFinder {
private final int numThreads; // number of threads
private final int range; // range to find prime numbers
private boolean[] primes; // array to store prime numbers
private int blockSize; // size of each block
private List<Thread> threads; // list of threads
public ParallelPrimeFinder(int numThreads, int range) {
this.numThreads = numThreads;
this.range = range;
this.primes = new boolean[range + 1]; // initialize boolean array to store prime numbers
this.blockSize = (range + numThreads - 1) / numThreads; // calculate block size
this.threads = new ArrayList<>(); // initialize list of threads
// Initialize primes array
for (int i = 2; i <= range; i++) {
primes[i] = true; // mark all numbers as prime
}
}
public List<Integer> getPrimes() throws InterruptedException {
// Create threads
for (int i = 0; i < numThreads; i++) {
int start = i * blockSize + 2; // calculate starting index of block
int end = Math.min((i + 1) * blockSize + 1, range); // calculate ending index of block
Thread thread = new Thread(() -> {
// Sieve of Eratosthenes algorithm
for (int j = 2; j * j <= end; j++) {
if (primes[j]) {
int startMultiple = (start / j) * j; // calculate smallest multiple of j that is >= start
if (startMultiple < j * j) {
startMultiple = j * j; // if startMultiple is less than j^2, set it to j^2
}
for (int k = startMultiple; k <= end; k += j) {
primes[k] = false; // mark multiples of j as composite
}
}
}
});
threads.add(thread); // add thread to list of threads
thread.start(); // start thread
}
// Wait for threads to finish
for (Thread thread : threads) {
thread.join(); // wait for thread to finish
}
// Create list of prime numbers
List<Integer> primeNumbers = new ArrayList<>();
for (int i = 2; i <= range; i++) {
if (primes[i]) {
primeNumbers.add(i); // add prime numbers to list
}
}
return primeNumbers;
}
}
The code above is a Java implementation of a parallel prime number finder using the Sieve of Eratosthenes algorithm.
- It uses multiple threads to speed up the calculation of prime numbers within a given range.
- The ParallelPrimeFinder class has two instance variables: numThreads and range. numThreads specifies the number of threads to be used for the calculation, and range specifies the upper limit of the range of prime numbers to find.
- The constructor initializes the primes boolean array to true for all indexes from 2 to range.
- The blockSize variable is calculated to divide the range of numbers equally among the threads, and a list of Thread objects is created.
- The getPrimes() method is used to start each thread and wait for them to finish.
- Each thread uses the Sieve of Eratosthenes algorithm to mark multiples of non-prime numbers as composite within its designated block of numbers.
- The program then creates a list of prime numbers by iterating over the primes boolean array and adding any true indexes to the list.
Overall, the code uses multiple threads to perform the Sieve of Eratosthenes algorithm on separate blocks of numbers, improving the performance of the prime number finder.
To Use above ParallelPrimeFinder Class to find prime numbers, the Main method is as follows:
import java.util.*;
public class Main {
static Scanner sc = new Scanner(System.in);
public static void main(String[] args) throws InterruptedException
System.out.println("Enter the range of prime numbers and No. of Threads to be used: ");
int N = sc.nextInt(); // Range of prime numbers
int numThreads = sc.nextInt(); // No. of Threads
ParallelPrimeFinder result = new ParallelPrimeFinder(numThreads, N);
List<Integer> Primeno = result.getPrimes();
for(int p : Primeno){
System.out.print(p+" ");
}
}
}
The code above is a simple Java program that uses the ParallelPrimeFinder class to find all prime numbers within a specified range using a user-defined number of threads.
- The Main class contains a main() method that prompts the user to enter the range of prime numbers and the number of threads to be used for the calculation.
- The program then creates an instance of the ParallelPrimeFinder class with the specified parameters and calls the getPrimes() method to obtain a list of prime numbers within the specified range.
- Finally, the program iterates over the list of prime numbers and prints each number to the console.
- The program uses a Scanner object to read user input and handle any input exceptions that may arise during runtime.
Look at the example output

Time & Space Complexity
Time Complexity:
- The time complexity of the ParallelPrimeFinder class is O(n log log n) because it uses the Sieve of Eratosthenes algorithm, which has a time complexity of O(n log log n).
- In the getPrimes method, the algorithm divides the range of numbers to find primes into blocks and assigns each block to a thread.
- The size of each block is blockSize = (range + numThreads - 1) / numThreads, which gives an approximately equal distribution of work among threads.
- The algorithm then applies the Sieve of Eratosthenes to each block independently in parallel, marking composite numbers in the primes array.
- Finally, it merges the prime numbers from each block into a single list of prime numbers.
- The time complexity of the getPrimes method is O(n log log n / numThreads), which is the time complexity of the Sieve of Eratosthenes algorithm divided by the number of threads used.
- However, the actual running time may depend on the number of available processor cores and the efficiency of the operating system in scheduling threads.
Space Complexity:
- The space complexity of the class is O(n), as it uses a boolean array of size n+1 to store whether a number is prime or not.
- The space complexity of the method is O(blockSize), as it uses a boolean array of size blockSize to store whether a number is prime or not for each thread.
Conclusion
- In conclusion, we have explored the Sieve of Eratosthenes algorithm, a simple and efficient way to find all prime numbers up to a given limit.
- We have also discussed how this algorithm can be implemented in parallel to improve its performance for large input sizes.
- We saw that multithreading can be used to divide the range of numbers into blocks and distribute the work across multiple threads to speed up the computation.
- However, we also noted that parallelization comes with overhead costs, such as increased memory usage and synchronization between threads, which can offset the benefits of parallel processing for small input sizes.
- Therefore, it is essential to carefully consider the input size and the number of threads used to achieve the best performance.
- In summary, the Sieve of Eratosthenes algorithm is a useful tool for finding prime numbers, and parallelization can significantly improve its performance for large input sizes.
- With the right approach and careful consideration of the input size and hardware resources, we can efficiently compute prime numbers using this algorithm.
