N-th root of a number

In this article, we have explained three different algorithms to find the N-th root of a number.

• Contents

1. using Binary Search
2. using Log
3. using Newton's method

• Pre-requisites

cube-root using binary-search

Conventions

Let's decide on some convention first,
we will take some number to calculate nth root on, we'll call it N and since,
then, we have to calculate nth root let that nth be n.
and also let's consider x will be our result.

Pre-Discussion

If you have read the cube-root using binary-search before this, we have talked about how we have a straight-up solution (formula) to calculate a root of any number and because of that calculating the n^th-root of a number requires guess and check approach and we're going to at 3 of the approaches here.

Other than Binary Search we're going to look at the Logarithmic method that you may have studied in your high school, where you take a $\log{}$ of a number and then you're done with the calculation you take anti-log and you get the answer to your original equation.

Another approach we're going to look at is the Newton's method which is better than binary search in many cases, we'll see that.
To understand Newton's method, you do require to be a little familiar with calculus and be able to visualize a function, ( Tension not! ) you can use any graphing tool online.

Binary Search

Here we search a $x$ through Binary Search which will satisfy the condition of $x^n = N$,
and this search happens on the space of $[1, N]$.
and yes, you can change your space search to something like $[1, N/2]$ only make sure that your space does not end up excluding, the $x$ we ought to find.

We will be using the same code from cube-root using binary-search with a few changes of course.

First, let's find the Perfect Root ( the one which doesn't have any decimal values ).

 1 def perfect_root(N, n):
 2    start, end = 1, N
 3    mid = (start + end) // 2
 4
 5    while mid != start and pow(mid, n) != N:
 6        if pow(mid, n) > N:
 7            end = mid
 8        else:
 9            start = mid
 10       mid = (start + end) // 2
 11  return mid

Here we have changed only two condition checks on lines 6 and 7.

Note: perfect_root will return a perfect root or the lower value.

Now, after this function, we will need one more function to find the root with some precision.
This function will search on space of $[0, 9]$, where it will change the power/precision meaning, after $[0, 9]$ we will search on $[0.0, 0.9]$ and then on $[0.00, 0.09]$ and so on.
In every search, the function will choose a value, which may create a perfect root or it will add the lower value to the previous root we found.

 1  def nth_root(N, n=2, precision=5):
 2     P = lambda a, b: a * 10 ** (-b)
 3
 4     x = perfect_root(N, n)
 5     if pow(x, n) == N:
 6         return x
 7
 8     for i in range(1, precision + 1):
 9         start, end, mid = 0, 9, 5
 10        current_N = lambda: pow(x + P(mid, i), n)
 11
 12        while start != mid:
 13            if current_N() > N:
 14                end = mid
 15            elif current_N() < N:
 16                start = mid
 17            elif current_N() == N:
 18                return x + P(mid, i)
 19
 20            mid = (start + end) // 2
 21
 22        x += P(mid, i)
 23
 24    return x

Time Complexity

The first thing we're using is binary search to find the perfect root, which will take a time of $\log_2{N}$, and then after that, we are using again the binary search on the space of $[0, 9]$ for the P times,
therefore,

Time Complexity: $O(\log_2{N} + P)$

Space Complexity

The Algorithm runs in constant complexity.

Space Complexity: $O(1)$

Log

Using $\log{}$ is simple than other mentioned methods in this article.
The Function we have is, $f(x) = \sqrt[n]{x}$

Let's apply $\log{}$ on it,

$$\log_{10}{f(x)} = \frac{1}{n}\log_{10}{x}$$

we can calculate $\log{x}$ by using the function log10 from the math module in python.
But after we're done with $\log{}$ we need to also calculate the anti-log of the result, this we can do by putting the result we received in the power of 10, because the base of our function is 10.
i.e.

$$\log_{10}{\sqrt[n]{x}} = \frac{1}{n}\log_{10}{x}$$
$$\sqrt[n]{x} = 10^{(\frac{1}{n}\log_{10}{x})}$$

Note: For the above thing pre-requisite is knowing, what log is?

1  from math import log10
2
3  def nth_root(N, n=2, P=5):
4     return round(pow(10, (1 / n) * log10(N)), P)

We talked in the beginning about how finding the root of a number doesn't have any formula, but here it seems that we do, but NO!
The $log$ itself has time-complexity of $log_{base}{N}$.

Newton's method

Newton's method is something could be used to find a value for x where y equals to zero, i.e. $$f(x) = 0$$

To find this we first need to guess a value for x that make $f(x) = 0$, and then from there, we get a new value for x, every time we calculate using Newton's method. And we repeat it until we get the same x as before.

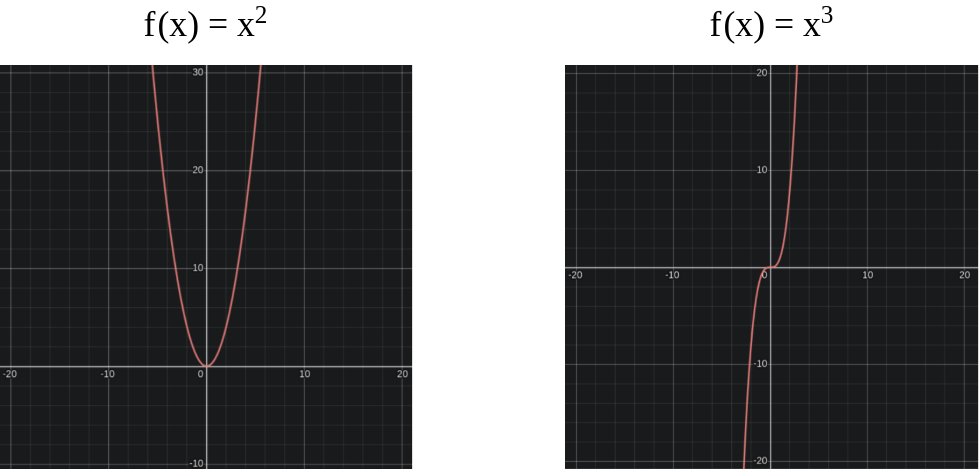
In our case the $f(x)$ we have is $x^n$, which would look something like.

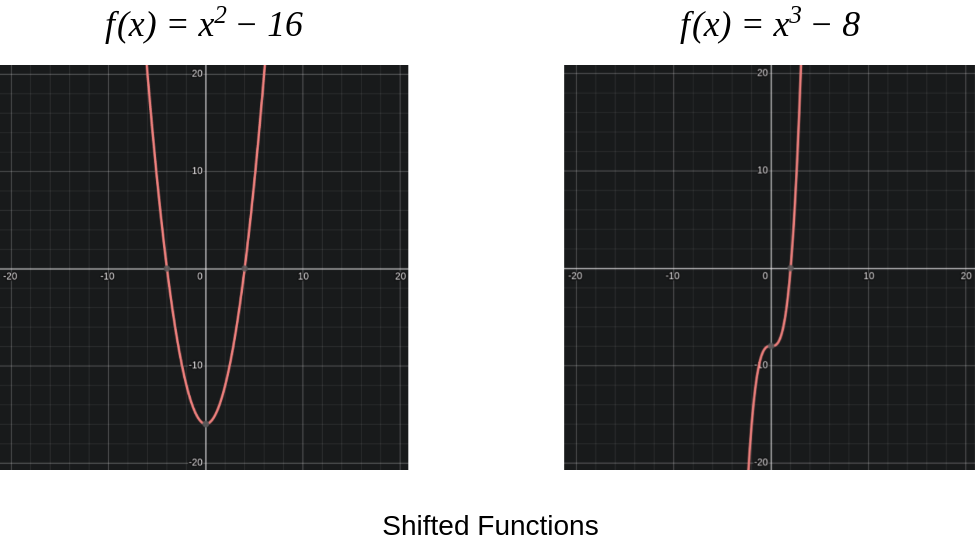
And after we shift the $f(x)$ with some number(N), then it looks something like.

Suppose we start with $x_0$ then,
$$x_1 = x_0 - \frac{f(x)}{f'(x)}$$
And when we reach the answer, the root we were looking for, then $f(x)$ produces $0$.
which causes $x_n$ to become equal to $x_{n-1}$ because $x_n = x_{n-1} - 0$.

And code would look something the following:

1  def nth_root(N, n=2, x=0, P=5):
2     if not n:
3        return 1
4     if x ** n == N:
5        return x
6     if not x or x <= 0:
7        x = N
8  
9     next_x = lambda: round(x - (pow(x, n) - N) / (n * pow(x, n - 1)), P)
10 
11    nx = next_x()
12    while x != nx:
13       x = nx
14       nx = next_x()
15 
16    return nx

Time Complexity

After every loop Newton's Method produces a value for x with a quadratic number of precision, i.e. for example we have x as 1.8 and we are doing nth_root(512, n=10, x=1.8, P=16) then this will produce something like the following:

                          Removing extras
x0 = 1.8
x1 = 1.8781174791713198  1.8 
x2 = 1.8664080886917562  1.866
x3 = 1.8660662651157902  1.86606
x4 = 1.8660659830738067  1.866065983073
x5 = 1.8660659830736148  1.8660659830736148

So, if we compare we see that number of precision that is from the correct answer is doubling,
This is why? (provided, the x only lacks precision), Newton's method requires $\log_2{P}$ loops to get to the answer.

therefore,

Time Complexity = $O(\log_2{P} * F(x))$

$F(x)$ is Time Complexity for the provided Function.

Space Complexity

Implementing Newton's method does not require any amount of extra memory,
therefore, usage of memory remains constant.
i.e.

Space Complexity = $O(1)$

An Idea

The higher the value of n gets the steeper the graph becomes, which means that Newton's Method would require more loops to get to the correct answer,
therefore, we could do one thing i.e use Binary Search for a correct answer with the precision of one and then plug the answer as $x_0$ to the Newton's Method.
And this should happen in $O(\log_2(N) + \log_2{P} * F(x))$ of complexity.

With this article at OpenGenus, you must have the complete idea of different approaches to find N-th root of a number.