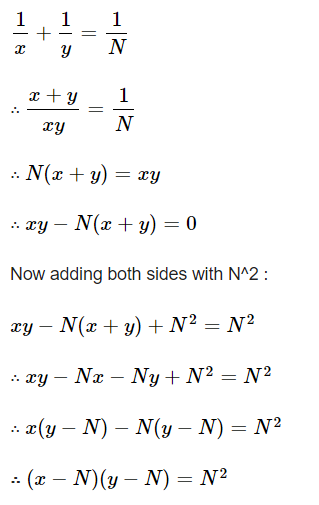Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explored two insightful approaches/ algorithms to find the Number of Ordered Solution Pairs (X, Y) satisfying 1/X + 1/Y = 1/N. This problem is used extensively in Astrophysics.
Table of contents:
- Problem Statement Definition
- Method 1: Using Number of divisors
- Method 2: Analyze equation
- Applications
Let us get started with Number of Ordered Solution Pairs (X, Y) satisfying 1/X + 1/Y = 1/N.
Problem Statement Definition
Given a positive integer N, the task is to find the number of pairs (X, Y) where both X and Y are positive integers, such that they satisfy the equation:
1/X + 1/Y = 1/N
There are two methods for finding the number of ordered pairs (x , y):
- Method 1: Using Number of divisors
- Method 2: Analyze equation
Let us look at both methods.
Method 1: Using Number of divisors
This method involves finding the number of divisors of N. Let us understand how this works mathematically:
Mathematical Formulation
From this equation we know that number of solutions will be the number of divisors of N. To find the number of divisors, we established that we could use the prime factorization to find the number of divisors such that if we have the number N we have
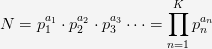
and then the number of divisors will be
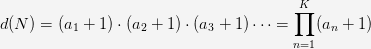
However, we are finding the divisors of n^2, so instead of factoring n^2 we will factor n and the number of factors of n^2 will then be
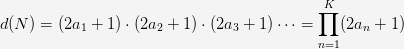
This is because
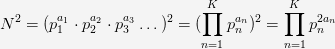
Now that we have understood how we got the final equation, let us see the algorithm to implement it
Algorithm
The algorithm for the approach given above is:
-
Find the prime-factors of N using the sieve of Eratosthenes-
- Make an array of size n+1.
- Initialize all values as 1.
- Traverse i from 2 to square root of n.
- If i divides n, mark all multiples of i as 0
-
Initialize total as 1
-
Traverse i from 2 to square root of n
-
If arr[i] = 1, then
- Initialize count = 0
- While i divides n
- n = n/p
- Increment count
- Multiply total with (2 * count +1) and store it in total
-
Display total
Implementation
Let us look at the implementation of this prgram in C++
#include <bits/stdc++.h>
using namespace std;
int Solutions(int n)
{
bool hash[n + 1];
memset(hash, true, sizeof(hash));
for (int p = 2; p * p < n; p++)
if (hash[p] == true)
for (int i = p * 2; i < n; i += p)
hash[i] = false;
int total = 1;
for (int p = 2; p <= n; p++) {
if (hash[p]) {
int count = 0;
if (n % p == 0) {
while (n % p == 0) {
n = n / p;
count++;
}
total = total * (2*count + 1);
}
}
}
return total;
}
int main()
{
int n = 24;
cout << "The number of solutions (x,y) for 1/x + 1/y = 1/" <<n<<" are: " <<Solutions(n);
return 0;
}
Output: The number of solutions (x,y) for 1/x + 1/y = 1/24 are: 21
Complexity
- Worst case time complexity:
Θ(n(log n)(log n)) - Average case time complexity:
Θ(n(log n)(log n)) - Best case time complexity:
Θ(n(log n)(log log n)) - Space complexity:
Θ(n)
Method 2: Analyze equation
In this method, we solve for only variable (x) by keying in y values which satisfy the equation.
Mathematical Formulation
1/X + 1/Y = 1/N
=> 1/X = 1/N – 1/Y
=> 1/X = (Y – N) / NY
=> X = NY / (Y – N)
X = [ NY / (Y – N) ] * (1)
=> X = [ NY / (Y – N) ] * [1 – N/Y + N/Y]
=> X = [ NY / (Y – N) ] * [(Y- N)/Y + N/Y]
=> X = N + N^2 / (Y – N)
-
Therefore, it can be observed that, to have a positive integer X, the remainder when N2 is divided by (Y – N) needs to be 0.
-
It can be observed that the minimum value of Y can be N + 1 (so that denominator Y – N > 0) and the maximum value of Y can be N^2 + N so that N^2/(Y – N) remains a positive integer ≥ 1.
Now that we have understood the constraints and how we arrived at the final equation, let us check the algorithm to implement this:
Algorithm
The algorithm for the approach given above is:
- Read the input n
- Initialize ans = 0
- Traverse y from n + 1 to n * n
- If (y-n) divides square of n, Then
- Increment ans
- Print ans
Implementation
Let us look at the implementation of this program in C++
#include <bits/stdc++.h>
using namespace std;
int Solutions(int n)
{
int ans = 0;
for (int y = n + 1; y <= n * n + n; y++) {
if ((n * n) % (y - n) == 0) {
ans += 1;
}
}
return ans;
}
int main()
{
int n = 24;
cout << "The number of solutions (x,y) for 1/x + 1/y = 1/" <<n<<" are: " <<Solutions(n);
return 0;
}
Output: The number of solutions (x,y) for 1/x + 1/y = 1/24 are: 21
Complexity
- Worst case time complexity:
Θ(log n) - Average case time complexity:
Θ(log n) - Best case time complexity:
Θ(log n) - Space complexity:
Θ(1)
Applications
- The ordered solution pairs of a variation of this equation are used extensively in Astrophysics.
- It is also used in solutions of differential equations.
Question
Find the count of solution of the equation 1/x +1/y =1/5
With this article at OpenGenus, you must have a strong idea of finding the Number of Ordered Solution Pairs (X, Y) satisfying 1/X + 1/Y = 1/N.