Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 25 minutes | Coding time: 10 minutes
In this article at OpenGenus, we shall see how to find the number of pairs in the array of length N whose sum is divisible by a certain given number (say K). We will take two approaches:
- Brute force approach O(N2) time and O(1) space
- Efficient approach O(N) time and O(K) time
This problem will give you a deep understanding of how division works and how other concepts like modulus come into picture. This is a must read if you want to master Algorithms.
For example:
arr[] = {1,2,4,5,6,7}
k=4;
so in this case (1,7),(2,6),(5,7) are the required pairs
as 1+7=8 is divisible by 4, 2+6=8 is divisible by 4, 5+7=12 is also divisible by 4.
so our output shall be = 3.
Brute force approach
In this approach we shall scan each and every element of the array and finally count the number of pairs that form to be in or favor. The steps are as follows:
- Generate all pairs in the list of N elements
- For each pair, add the numbers and check if it is divisible by K
- Keep a count of number of pairs which satisfy the conditions
Note that generating all pairs is simple as you just need to pair i-th element with j-th element where j > i, j < N and i ranges from 0 to N-1. A nested loop is enough for generating all pairs like:
for i from 0 to N-1
for j from i+1 to N-1
pair = (element[i] , element[j])
Code implementation:
#include<iostream>
using namespace std;
int main()
{
int arr[100];
int k,n,c=0;
cout<<"enter the size of the array"<<endl;
cin>>n;
cout<<"enter the array element"<<endl;
for(int i=0;i<n;i++)
{
cin>>arr[i];
}
cout<<"enter the value of k"<<endl;
cin>>k;
for(int i=0;i<n;i++)
{
for(int j=i+1;j<n;j++)
{
if((arr[i]+arr[j])%k==0)
c++;
}
}
cout<<"the number of pairs="<<c<<endl;
return 0;
}
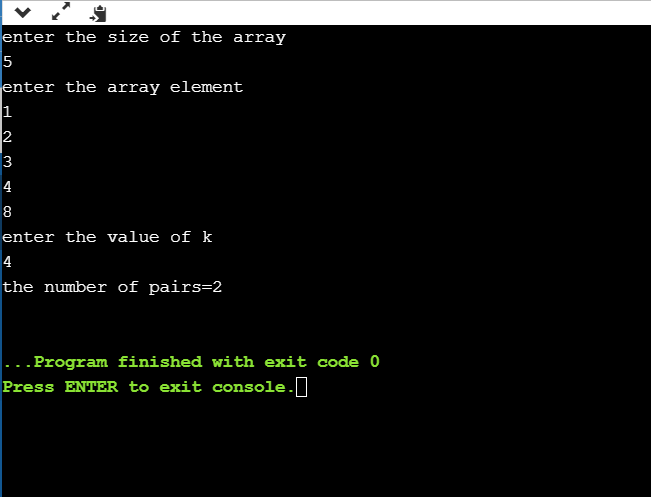
Output:
Complexity:
- Time complexity: O(N * N)
- Space complexity: O(1)
Efficient approach
In this approach we will use hashing method.What we are going to do is keep the elements in different cells of an array , this will be unique because we will separate them on the basis of their mod value with k. When a number is divided by K then the remainder may be 0, 1, 2, upto (k-1). We take an array remf[]of size k. At first we initialize each element with 0 and increase the value of remf[A[i]%K], this calculates the occurrences of i mod k.
remf[i] = number of elements with remainder i
The key idea is to use remf to get our answer. The idea is the a element from remf[i] will form a valid pair with a number from remf[j] if and only if:
i + j = K or 0
This is because consider two numbers N1 and N2 and a divisor K. If the remainder of N1 on dividing by K is R1 and similarly, the remainder of N2 is R2.
-
If N1 and N2 are divisible by K, then both R1 = 0 and R2 = 0. In this case, the remainder of dividing N1+N2 by K will also be 0.
-
If N1 is perfectly divisible by K but N2 is not, then R1 = 0 but R2 != 0. In this case, the remainder on dividing N1+N2 by K will be R2.
-
If both N1 and N2 are not divisible, then N1+N2 can be divisible by K only if R1 + R2 = K (or a multiple of K in general) and this is because K is perfectly divisible by K.
Let us understand this:
Let:
A[] = {9,4,2,8,0}, K = 3
This simply means we have to find the pairs whose sum is divisible by k=4;
Now first we take an frequency array remf[] where shall store the frequecies of all the remainders when each number is divided by k.
so its obvious that since we have taken k=3, so the remainders can maximum be 2 and min be 0 i.e [0,1,2]
so when we iterate over each digit in array A[].
we get:
i=0 A[i]=9 so 9%3=0 therefore remf[0]=1.
i=1 A[i]=4 so 4%3=1 therefore remf[1]=1.
i=2 A[i]=2 so 2%3=2 therefore remf[2]=1.
i=3 A[i]=8 so 8%3=2 therefore remf[2]=2.
i=4 A[i]=0 so 0%3=0 therefore remf[0]=2.
so the hash table would look as such:
| A[i] % k | remf[ A[i] % k ] |
|---|---|
| 0 | 2 |
| 1 | 1 |
| 2 | 2 |
Now if a pair is to be divisible by k then the sum of the remainder's shall be equal to k or 0.
So we consider the cases:
When both the remainder's of the pair are 0:
In such a case the number of valid pairs are remf[0] * remf[0]-1.
If there are n digits having 0 as their remainder, then the number of valid pairs are n*(n-1).
When the sum of remainder's of the pair is equal to k:
In such a case where the remainder's of the pair add upto make k.Then the pair is valid.
And then we just put couple of conditions to check the hash table and find the pairs that add up and are divisible by 3.
Like, if we get a pair whose remainders are 1 and 2 then the pair can a valid pair because they add up to become 3 which is divisible by 3.
So Then we get an answer of 3 valid pairs for {9,4,2,8,0}
Code implementation:
#include <bits/stdc++.h>
using namespace std;
int pair_calc(int A[], int n, int K)
{
int remf[K] = { 0 };
for (int i = 0; i < n; i++)
remf[A[i] % K]=remf[A[i] % k]+1; // caculating the rem frequency
int sum = remf[0] * (remf[0] - 1) / 2; //if in case the both the pairs are // divisible by k
//now we just need to count i and k-i pairs
for (int i = 1; i <= K / 2 && i != (K - i); i++)
sum += remf[i] * remf[K - i];
if (K % 2 == 0) //if k is even
sum += (remf[K / 2] * (remf[K / 2] - 1) / 2);
return sum;
}
int main()
{
int arr[] = { 1,3,5,7,9,4,2,8,0 };
int n = 9;
int K = 4;
cout << pair-calc(arr, n, K);
return 0;
}
Output:
9
complexity:
Time complexity: O(N)
Space complexity: O(K)
This was the efficient algorithm which has the best complexity to solve this problem. I hope you got this to the best. Happy coding.