
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have designed and implemented Quick Sort algorithm in C++ Programming Language to use the concept of template to make Quick Sort generic/ independent of input datatype.
Table of contents
- Introduction
- QuickSort algorithm
- QuickSort with STL
1. Introduction
There are few algorithms for sorting, QuickSort is one of the fastest way to do so. It's logic uses a partition function to split an array into two parts having the elements from the left part less than a "dividing line" and the second part having elements greater than that.
Computing a "dividing line", how C.A.R Hoare named it in his paper at the age of 22 when he was a student, will have some impact in the performance of the algorithm.
2. QuickSort algorithm
The algorithm uses divide et impera technique, and calls the function recursively for the two parts spplited by the partition/pivot function.
Pseudocode
array A[n]
p <- 1
u <- n
QuickSort(A,p,u)
if p<u then
k <- pivot(A,p,u)
QuickSort(A,p,k-1)
QuickSort(A,k+1,u)
end if
end QuickSort
Pivot(A,p,u)
i <- p
j <- u
cp <- 0
cu <- -1
loop
if i < j
A[i] <-> A[j]
cp <-> -cu
end if
i <- i + cp
j <- j + cu
end loop
return j
end Pivot
Study case: array[6] = {5,3,2,8,7,1}
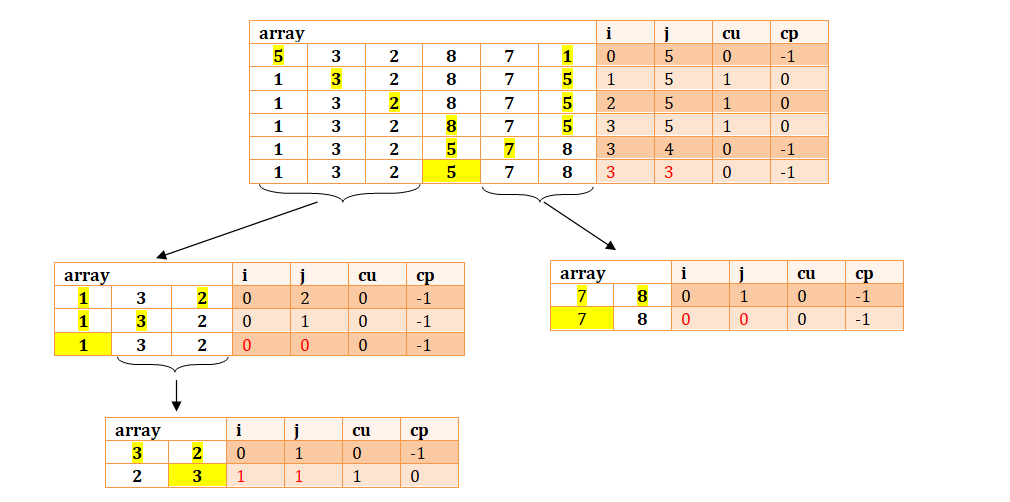
A way of implementation
For the next implementation I have used a class which has at its private members a pointer to the array to be sorted and the partition/pivot function and, as public members a constructor which initializes the pointer and the quicksort function.
#include <iostream>
using namespace std;
class Sort
{
private:
int *array;
int pivot(int p, int u)
{
int i=p, j=u, count_p=0, count_u =-1;
int temp1, temp2;
while(i<j)
{
if(array[i] > array[j])
{
temp1 = array[i]; array[i] = array[j] ; array[j] = temp1;
temp2 = count_p; count_p = - count_u; count_u = - temp2;
}
i+= count_p;
j+= count_u;
}
return j;
}
public:
Sort(int *array)
{
this->array = array;
}
void quickSort( int p, int u)
{
if(p<u)
{
int k = pivot(p,u);
quickSort(p, k-1);
quickSort(k+1,u);
}
}
};
int main()
{
int a[] = {-142,100,-183,229,-10,225,-100,0,-1,1,10,5,-12,-1,0};
int length = 15;
Sort s(a);
s.quickSort(0,length-1);
for(int i=0;i<length; i++)
cout << a[i] << " ";
return 0;
}
Output:
-183 -142 -100 -12 -10 -1 -1 0 0 1 5 10 100 225 229
3. QuickSort with STL
An STL or a Standard Template Library is a way to work with different data types without changing the declaration of an object or function.
There are two types of templates
- template functions
template <class identifier> function_declaration;
template <typename identifier> function_declaration;
- class template
template <class T>
class mypair {...};
A way of implementation
For this tutorial I've used for simplicity the class template option as I already have a definition of a class, and the only thing that needs to be changed is the type of the array.
#include <iostream>
using namespace std;
template<class myType>
class Sort
{
private:
myType *array;
int pivot(int p, int u)
{
int i=p, j=u, count_p=0, count_u =-1;
int temp1, temp2;
while(i<j)
{
if(array[i] > array[j])
{
temp1 = array[i]; array[i] = array[j] ; array[j] = temp1;
temp2 = count_p; count_p = - count_u; count_u = - temp2;
}
i+= count_p;
j+= count_u;
}
return j;
}
public:
Sort(myType *array)
{
this->array = array;
}
void quickSort( int p, int u)
{
if(p<u)
{
int k = pivot(p,u);
quickSort(p, k-1);
quickSort(k+1,u);
}
}
};
int main()
{
int a[] = {-142,100,-183,229,-10,225,-100,0,-1,1,10,5,-12,-1,0};
int length = 15;
Sort<int> s(a);
s.quickSort(0,length-1);
for(int i=0;i<length; i++)
cout << a[i] << " ";
return 0;
}
Output:
-183 -142 -100 -12 -10 -1 -1 0 0 1 5 10 100 225 229
The downsize of the previous example is that it works only for int type because at some point we will need to interchange the elements of the array and the comparation sign ">" works only for numbers.What if we will compare strings, or any other object ?
The next implementation will move forward the power of using template, and will answer to our question.
So, basically we will need to find a way to compare elements regarding of their data types.
My solution was to declare a pointer to a function pf as a member of our class that will point later to a comparation function defined separately for each case, maxNumber for numbers comparation and maxString for the string comparation. Of course it can be added any kind of rule of comparation as long as it will respect the logic: something needs to be less than something else.
A way of implementation
#include <iostream>
using namespace std;
template<class myType>
class Sort
{
private:
myType *array;
bool (*pf)(myType *a, myType *b);
int pivot(int p, int u )
{
int i=p, j=u, count_p=0, count_u =-1;
myType temp1;
int temp2;
while(i<j)
{
if( pf( &array[i] , &array[j]) )
{
temp1 = array[i]; array[i] = array[j] ; array[j] = temp1;
temp2 = count_p; count_p = - count_u; count_u = - temp2;
}
i+= count_p;
j+= count_u;
}
return j;
}
public:
Sort(myType *array)
{
this->array = array;
}
void quickSort( int p, int u)
{
if(p<u)
{
int k = pivot(p,u);
quickSort(p, k-1);
quickSort(k+1,u);
}
}
void setMaxFunction(bool (*pf)(myType *a, myType *b))
{
this->pf = pf;
}
};
bool maxNumber(int *a, int *b)
{
return *a > *b;
}
bool maxString(string *a, string *b)
{
return a->compare(*b)>0 ? true : false;
}
int main()
{
int a[] = {-142,100,-183,229,-10,225,-100,0,-1,1,10,5,-12,-1,0};
int length = 15;
Sort<int> s1(a);
s1.setMaxFunction(maxNumber);
s1.quickSort(0,length-1);
for(int i=0;i<length; i++)
cout << a[i] << " ";
cout<<endl;
string ss[] = {"Ana","has","blue","eyes"};
length = 4;
Sort<string> s2(ss);
s2.setMaxFunction(maxString);
s2.quickSort(0,length-1);
for(int i=0;i<length; i++)
cout << ss[i] << " ";
return 0;
}
Output:
-183 -142 -100 -12 -10 -1 -1 0 0 1 5 10 100 225 229
Ana blue eyes has
With this article at OpenGenus, you must have the complete idea of implementing Quick Sort in C++ Programming Language using the concept of template.
