In this article, we will take a look at the implementation of Bubble Sort in C++ using the concepts of OOP and template.

By the end of this article, you should have a good understanding of what Bubble Sort is, how it works, and its strengths and weaknesses. You will also be able to implement Bubble Sort in your own code and use it to sort arrays efficiently.

Table of contents:

• Introduction
• How Bubble Sort works
• Time and space complexity
• Implementation of Bubble Sort
• Conclusion

Introduction

Bubble Sort is a simple, popular and intuitive sorting algorithm that is taught in computer science courses. It gets its name from the way that larger elements in an array "bubble" to the top of the array(at the end) during each iteration of the algorithm. The basic idea behind Bubble Sort is to repeatedly compare adjacent elements in an array and swap them if they are in the wrong order, until the entire array is sorted. It is often used as a benchmark algorithm for measuring the performance of other sorting algorithms.

How Bubble Sort works

Bubble Sort is a comparison-based sorting algorithm that works by repeatedly swapping adjacent elements in an array if they are in the wrong order. The algorithm iterates over the entire array multiple times, with each iteration comparing adjacent elements and swapping them if necessary.

Here are the steps to perform Bubble Sort on an array of n elements:

• Start at the beginning of the array (i = 0).
• Compare the first and second elements of the array. If the first element is greater than the second element, swap them.
• Move to the next pair of adjacent elements and repeat step 2 until you reach the end of the array.
• At this point, the largest element in the array is at the end of the array.
• Repeat steps 1-4 for the entire array, except for the last element that was sorted in the previous iteration.
• Continue repeating steps 1-5 until the entire array is sorted.
• At each iteration of Bubble Sort, the largest unsorted element is "bubbled up" to the end of the array. Therefore, after each iteration, the end of the array contains the sorted elements, and the rest of the array contains the unsorted elements

Time and space complexity

• Time Complexity:

Bubble Sort has a worst-case and average-case time complexity of O(n^2), where n is the number of elements in the array. This means that the time it takes to sort an array using Bubble Sort increases quadratically as the size of the array increases. In the worst case scenario, where the array is in reverse order, Bubble Sort will make n*(n-1)/2 comparisons and swaps, resulting in a time complexity of O(n^2).

• Space Complexity:

The space complexity of Bubble Sort is O(1), which means that the algorithm uses a constant amount of extra space to perform the sort. Bubble Sort does not require any additional memory allocations, and all sorting is performed in-place, meaning that the original array is modified directly.

Implementation of Bubble Sort

• Normal function based approach:

#include <iostream>
using namespace std;

void bubbleSort(int arr[], int size)
{
    for (int i = 0; i < size - 1; i++)
    {
        for (int j = 0; j < size - i - 1; j++)
        {
            if (arr[j] > arr[j + 1])
            {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

int main()
{
    int arr[] = {10, 50, 40, 5, 14, 11, 90};
    int n = sizeof(arr) / sizeof(arr[0]);

    bubbleSort(arr, n);

    cout << "Sorted array: ";
    for (int i = 0; i < n; i++)
    {
        cout << arr[i] << " ";
    }
    cout << endl;

    return 0;
}

• The function bubbleSort takes two arguments - an integer array arr and its size size. This function performs the sorting operation on the given array using the Bubble Sort algorithm.
• The outer loop in bubbleSort iterates size-1 times. The loop variable i keeps track of the number of passes made over the array. Since each pass puts the largest element at the end of the array, we can stop the loop after size-1 iterations.
• The inner loop in bubbleSort iterates over the unsorted part of the array. Since each pass puts the largest element at the end, we don't need to iterate over the sorted part of the array. Hence, the loop variable j runs from 0 to size-i-1.
• The if statement inside the inner loop checks if the adjacent elements are in the correct order or not. If the element at index j is greater than the element at index j+1, then we swap them using a temporary variable temp.
• After the inner loop completes, the largest element has been placed at the end of the unsorted part of the array. Hence, we don't need to consider that element in the subsequent passes. We move to the next pass by incrementing the loop variable i in the outer loop.

• Using OOP and template

#include <iostream>
using namespace std;

template <class T>

class BubbleSort {
private:
    T* arr;
    int size;
public:
    BubbleSort(T* a, int s) {
        arr = a;
        size = s;
    }

    void sort() {
        for (int i = 0; i < size - 1; i++) {
            for (int j = 0; j < size - i - 1; j++) {
                if (arr[j] > arr[j + 1]) {
                    T temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
    }

    void display() {
        for (int i = 0; i < size; i++) {
            cout << arr[i] << " ";
        }
        cout << std::endl;
    }
};

int main() {
    int arr[] = {10, 50, 40, 5, 14, 11, 90};
    int n = sizeof(arr) / sizeof(arr[0]);

    BubbleSort<int> bs(arr, n);
    cout<<"Before sorting"<<endl;
    bs.display();
    cout<<"After sorting"<<endl;
    bs.sort();
    bs.display();

    return 0;
}

Output

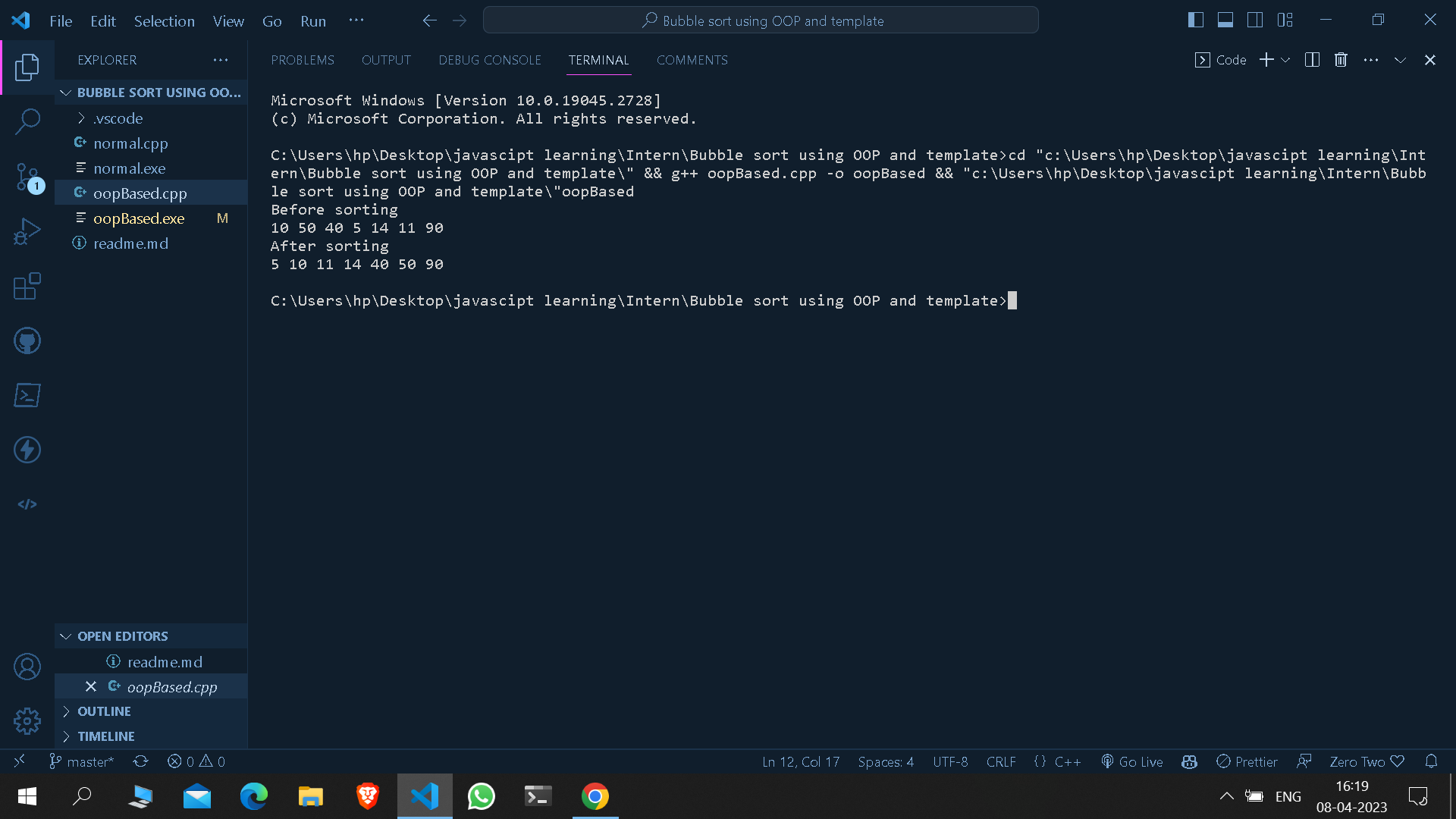
The main difference between these two codes is the use of OOP and templates in the second code, which makes the code more modular, reusable, and generic. By using OOP concepts, the second code provides better encapsulation, data abstraction, and data hiding. Templates, on the other hand, make the code more generic, so it can handle any type of array, not just integers.

Conclusion

With this article at OpenGenus, you must have the complete idea of implementing Bubble Sort in C++ Programming Language.

Overall, Bubble Sort is not an efficient algorithm in terms of time complexity, especially for large arrays. However, its simple implementation and low space complexity make it useful in certain situations where the size of the input is small, or where simplicity and ease of implementation are more important than performance. Additionally, Bubble Sort can be useful as a benchmark algorithm for comparing the performance of other sorting algorithms.