In this article at OpenGenus, we will explore the implementation of Quick Sort in Python using the principles of Object-Oriented Programming (OOP). By utilizing classes and objects, we'll implement the Quick Sort algorithm to efficiently sort arrays or lists of elements.

Table of contents:

1. Introduction
2. Solution
3. Quiz

Introduction

Quick Sort is a widely used sorting algorithm that follows the divide-and-conquer approach to sort an array or list of elements. The Quick Sort algorithm works by selecting a pivot element from the array and partitioning the other elements into two sub-arrays, according to whether they are less than or greater than the pivot. The sub-arrays are then recursively sorted using the same algorithm. This process continues until the entire array is sorted.

Algorithm

1. Choose a pivot element from the array (usually the last element, but other approaches are also possible).
2. Partition the array into two sub-arrays: elements smaller than the pivot and elements greater than the pivot.
3. Recursively apply the above steps to the sub-arrays until the base case is reached (sub-arrays with zero or one element are considered sorted).
4. Combine the sorted sub-arrays to obtain the final sorted array.

The key steps in the partitioning process involve rearranging the elements such that all elements smaller than the pivot come before it, and all elements greater than the pivot come after it. This ensures that the pivot element is in its final sorted position.

Solution

In Python, there are several ways to implement the Quick Sort algorithm. Here are two common types of implementation:

Recursive Implementation

The recursive implementation of Quick Sort follows the divide-and-conquer approach. It uses a recursive function to divide the array into smaller sub-arrays, sort them independently, and then combine them to obtain the final sorted array.

1. Select a pivot element from the array.
2. Partition the array into two sub-arrays: elements smaller than the pivot and elements greater than the pivot.
3. Recursively apply the above steps to the sub-arrays until the base case is reached (sub-arrays with zero or one element are considered sorted).
4. Combine the sorted sub-arrays to obtain the final sorted array.

    def quick_sort_recursive(self, low, high):
        if low < high:
            pivot = self.partition(low, high)

            self.quick_sort_recursive(low, pivot - 1)
            self.quick_sort_recursive(pivot + 1, high)

The quick_sort_recursive method is a recursive implementation of Quick Sort. It takes the low and high indices as arguments and recursively partitions and sorts the sub-arrays until the base case is reached.

Iterative Implementation

The iterative implementation of Quick Sort uses a stack or an auxiliary data structure to simulate the recursive function calls in an iterative manner. It avoids recursion by using loops and stack operations to handle the partitioning and sorting of sub-arrays.

1. Create an empty stack and push the initial boundaries of the array onto the stack (e.g., the lower and upper indices).
2. While the stack is not empty, pop the boundaries from the stack.
3. Partition the array based on the popped boundaries, obtaining the pivot element's final position.
4. Push the boundaries of the sub-arrays resulting from the partition onto the stack.
5. Repeat the above steps until the stack is empty.

    def quick_sort_iterative(self, low, high):
        stack = [(low, high)]

        while stack:
            low, high = stack.pop()

            if low < high:
                pivot = self.partition(low, high)

                stack.append((low, pivot - 1))
                stack.append((pivot + 1, high))

The quick_sort_iterative method is an iterative implementation of Quick Sort. It uses a stack to simulate the recursive function calls. It repeatedly pops boundaries from the stack, partitions the array, and pushes new boundaries onto the stack until the stack is empty.

Class Definition

class QuickSort:
    def __init__(self, array):
        self.array = array

The QuickSort class is defined. It has a constructor (init method) that takes an input array and initializes the class with it. The input array is stored as an instance variable called array.

Partition Function

def partition(self, low, high):
    i = low - 1
    pivot = self.array[high]

    for j in range(low, high):
        if self.array[j] <= pivot:
            i += 1
            self.array[i], self.array[j] = self.array[j], self.array[i]

    self.array[i + 1], self.array[high] = self.array[high], self.array[i + 1]
    return i + 1

The partition method is a helper function used to divide the array into two halves based on a pivot element. It takes two parameters, low and high, representing the lower and higher bounds of the current partition.

The method selects the pivot as the last element of the current partition (pivot = self.array[high]). It then iterates over the subarray from low to high-1. If an element is smaller than or equal to the pivot, it swaps the element with the element at index i+1. This ensures that elements smaller than the pivot are placed before the pivot in the array. Finally, it swaps the pivot element with the element at index i+1 to position the pivot at its correct sorted position. The method returns the index of the pivot.

Recursive Sort Call

def sort_recursive(self):
    self.quick_sort_recursive(0, len(self.array) - 1)
    return self.array

The sort_recursive method is a convenience method that calls the quick_sort_recursive method to perform a recursive QuickSort on the entire array. It starts with the initial lower bound of 0 and the higher bound as the last index of the array. It then returns the sorted array.

Iterative Sort Call

def sort_iterative(self):
    self.quick_sort_iterative(0, len(self.array) - 1)
    return self.array

The sort_iterative method is another convenience method that calls the quick_sort_iterative method to perform an iterative QuickSort on the entire array. It starts with the initial lower bound of 0 and the higher bound as the last index of the array. It then returns the sorted array.

Quick Sort Implementation

array = [6, 2, 9, 1, 5, 10, 8]

qs_recursive = QuickSort(array)
sorted_array_recursive = qs_recursive.sort_recursive()
print("Sorted Array (Recursive):", sorted_array_recursive)

qs_iterative = QuickSort(array)
sorted_array_iterative = qs_iterative.sort_iterative()
print("Sorted Array (Iterative):", sorted_array_iterative)

An example array [6, 2, 9, 1, 5, 10, 8] is created. Then, two instances of the QuickSort class are created: qs_recursive and qs_iterative. These instances are initialized with the example array.

The sort_recursive method is called on the qs_recursive instance to obtain the sorted array recursively. It is stored in the sorted_array_recursive variable. The sort_iterative method is called on the qs_iterative instance to obtain the sorted array iteratively. It is stored in the sorted_array_iterative variable. Finally, the sorted arrays are printed to the console using print statements.

Complete Implementation

class QuickSort:
    def __init__(self, array):
        self.array = array

    def partition(self, low, high):
        i = low - 1
        pivot = self.array[high]

        for j in range(low, high):
            if self.array[j] <= pivot:
                i += 1
                self.array[i], self.array[j] = self.array[j], self.array[i]

        self.array[i + 1], self.array[high] = self.array[high], self.array[i + 1]
        return i + 1

    def quick_sort_recursive(self, low, high):
        if low < high:
            pivot = self.partition(low, high)

            self.quick_sort_recursive(low, pivot - 1)
            self.quick_sort_recursive(pivot + 1, high)

    def quick_sort_iterative(self, low, high):
        stack = [(low, high)]

        while stack:
            low, high = stack.pop()

            if low < high:
                pivot = self.partition(low, high)

                stack.append((low, pivot - 1))
                stack.append((pivot + 1, high))

    def sort_recursive(self):
        self.quick_sort_recursive(0, len(self.array) - 1)
        return self.array

    def sort_iterative(self):
        self.quick_sort_iterative(0, len(self.array) - 1)
        return self.array

array = [6, 2, 9, 1, 5, 10, 8]

qs_recursive = QuickSort(array)
sorted_array_recursive = qs_recursive.sort_recursive()
print("Sorted Array (Recursive):", sorted_array_recursive)

qs_iterative = QuickSort(array)
sorted_array_iterative = qs_iterative.sort_iterative()
print("Sorted Array (Iterative):", sorted_array_iterative)

Output

Sorted Array (Recursive): [1, 2, 5, 6, 8, 9, 10]
Sorted Array (Iterative): [1, 2, 5, 6, 8, 9, 10]

Time and Space Complexity

Time Complexity   : 
* Best Case: O(n log n), where n is the number of elements in the array
* Avearge Case: O(n log n), where n is the number of elements in the array
* Worst Case: O(n^2), where n is the number of elements in the array
Space Complexity  : O(n), where n is the number of elements in the array

Output Explanation

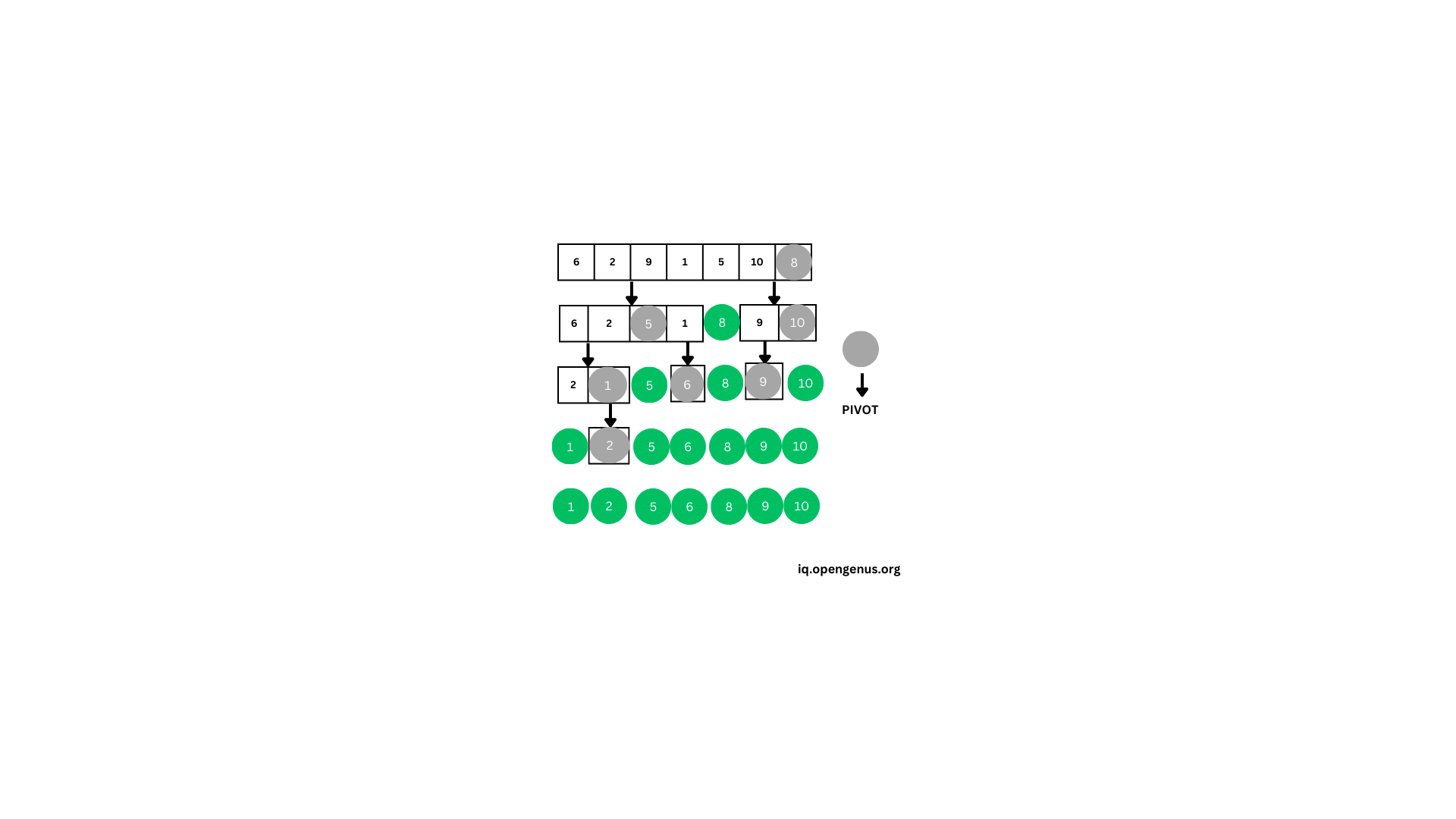
• Consider the input array: [6, 2, 9, 1, 5, 10, 8].
• Select a pivot element from the array, let's choose the last element (8 in this case).
• Rearrange the elements such that all elements smaller than the pivot are to its left, and all elements greater than the pivot are to its right.
• Left Sub-array [2, 1, 5]: The pivot element is 5 (the last element). Rearrange the elements to create sub-arrays with elements less than 5 and elements greater than 5.
• Right Sub-array [9, 10]: The pivot element is 10 (the last element). Rearrange the elements to create sub-arrays with elements less than 10 and elements greater than 10.
• Combine the sorted sub-arrays to obtain the final sorted array: [1, 2, 5, 6, 8, 9, 10].

Use of OOP Concepts

• Class: The QuickSort class represents the Quick Sort algorithm.

• Attributes: The class has an attribute self.array, which stores the array to be sorted. This encapsulates the data related to the sorting process within the class.

• Methods: The class has methods such as partition, quick_sort_recursive, and quick_sort_iterative, which represent the steps of the Quick Sort algorithm.

• Encapsulation: By organizing the Quick Sort algorithm within a class, the details of the sorting logic are encapsulated within the class.

• Abstraction: The class abstracts away the implementation details of the Quick Sort algorithm, making it easier for users to understand and use the sorting functionality.

Quiz