Before diving into what a radix tree is, it would be better for you to understand what a trie is since a radix tree is fundamentally a compact trie.

Radix tree is the compressed version of Trie data structure and is, also, known as Patricia trie.

Trie

OpenGenus has an article on trie already, but I'll explain it as simple and brief as possible. Trie
A trie is a tree-like data structure that primarily handles strings for look ups by looking at an incrmemental prefix of the input as the key.

Incremental prefix as in, once we looked at the prefix, we will continue with what's after the prefix as that will serve as the new prefix to compare and continue this process until a terminating condition is met.

It's important to note that there are different implementation variations of a trie which led way to different names, but all tries will have nodes and edges to traverse the tree-like structure.

A trie will often implement 3 main functions: insert, delete, and search.
Tries can offer additional functionalities, but we will keep it simple by only looking at the 3 main functions.

Radix Tree

As briefly mentioned before, a radix tree is a compact version of a trie. A trie is very space inefficient as often times you only store 1 character in an edge. A radix tree takes advantage of this and will store multiple characters / string of text in an edge instead to reduce the number of extra edges and nodes needed while still maintaining the same representational meaning along with the performance of a trie. At worst case scenario, a radix tree will be a trie.

Here is an example of a radix tree. This tree starts off with a root node that has edges. Each edge has a prefix string to compare.
- Ignore the edge that has no prefix string attached.

Characteristics
For our example of a radix tree for the following functions and implementation, we will use these characteristics:

• Every node can have edges and will have a flag to indicate if it's an end to a word.
• Every edge will have a string of characters and a node that it leads to.

Search

Lets say we wanted to see if a certain word existed in a radix tree.
Take for instance the example from below:

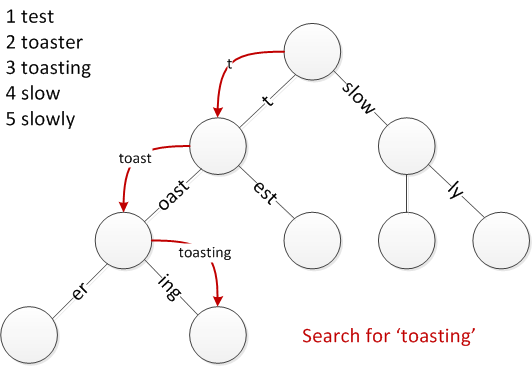
From the picture above, we are looking for the word "toasting".
Starting from the root, we find a prefix to "toasting" which is "t" so we take that edge and our resulting word we are looking at is "oasting" because we removed the prefix "t". Next we find a prefix for "oasting" which happens to be "oast", move onto the next node with our new word to look for "ing". We then look for an edge with a prefix to "ing" and find "ing" thus we move onto the next node with "" as our new word. We terminate our search and in this case, that word exists (the node isn't indicated as a word node but it is a word in this example).

There are cases where words are prefixes of other words which may exist such as "toast" for "toaster", however nodes often have an internal mechanic to check if it contains the word to help indicate words that are prefixes for other words as a word. Check insert to see more of an explanation as this is a case that can occur.

Insert

The images will be based on the characteristics we described earlier.

• Normal insert where the node has no edges that have a prefix to the word.

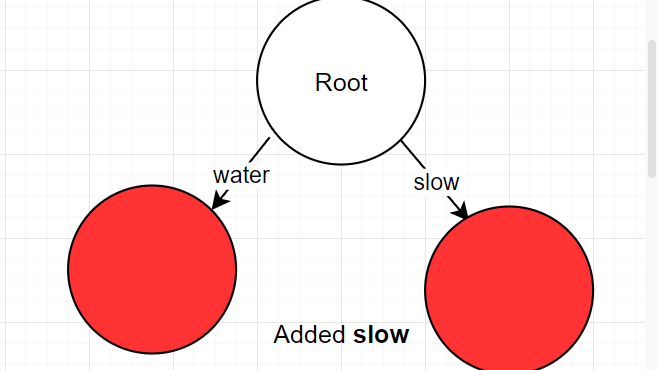
• Another normal insert

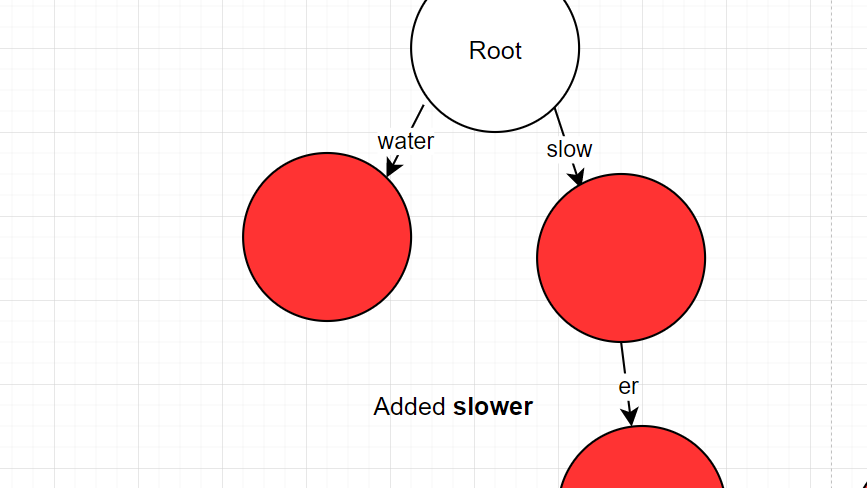
• Case 1: The prefix completely matches the first part of the word, but there are still leftover parts to the word.

• Process:

  • "slower" -> found "slow" as prefix
    • remove prefix from the current input
  • "er" -> normal insert

• Case 2: The word matches the prefix but the prefix has leftover parts (the word is shorter than the prefix)

• Imagine if it were "slower" inserted first, then "slow" was inserted second.

• process:

  • found "slower" as prefix, but the input: "slow" is smaller than the prefix, so split "slower"
    • splitting "slower" with "slow" into "slow" -> "er"

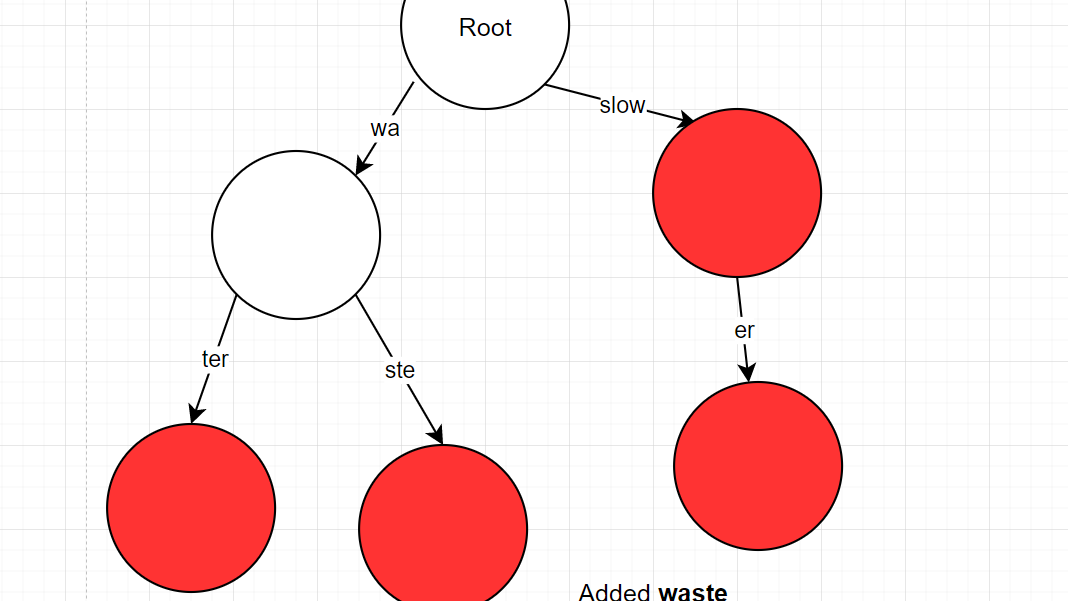
• Case 3: The prefix has a mismatch with the word
• Process:
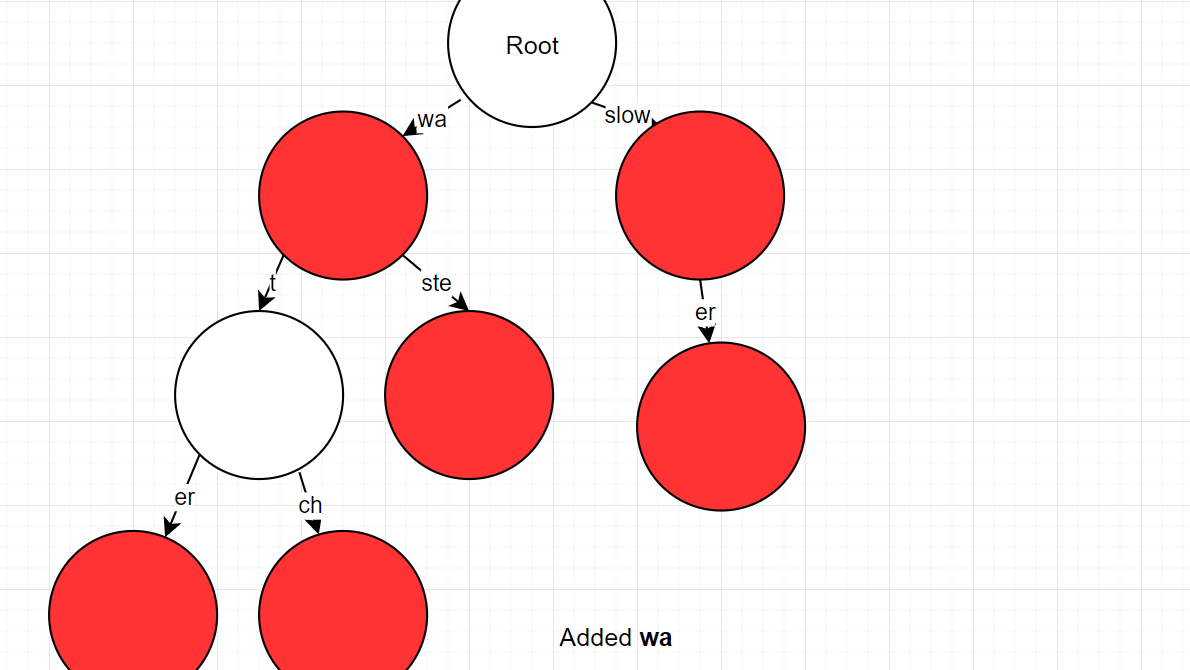
  • "waste" -> found "water" but mismatch "wat" != "was"
    • "wa" was previous matching prefix
      • must split "water" into "wa" and "ter" and keep the property as a word
  • "ste" -> noraml insert

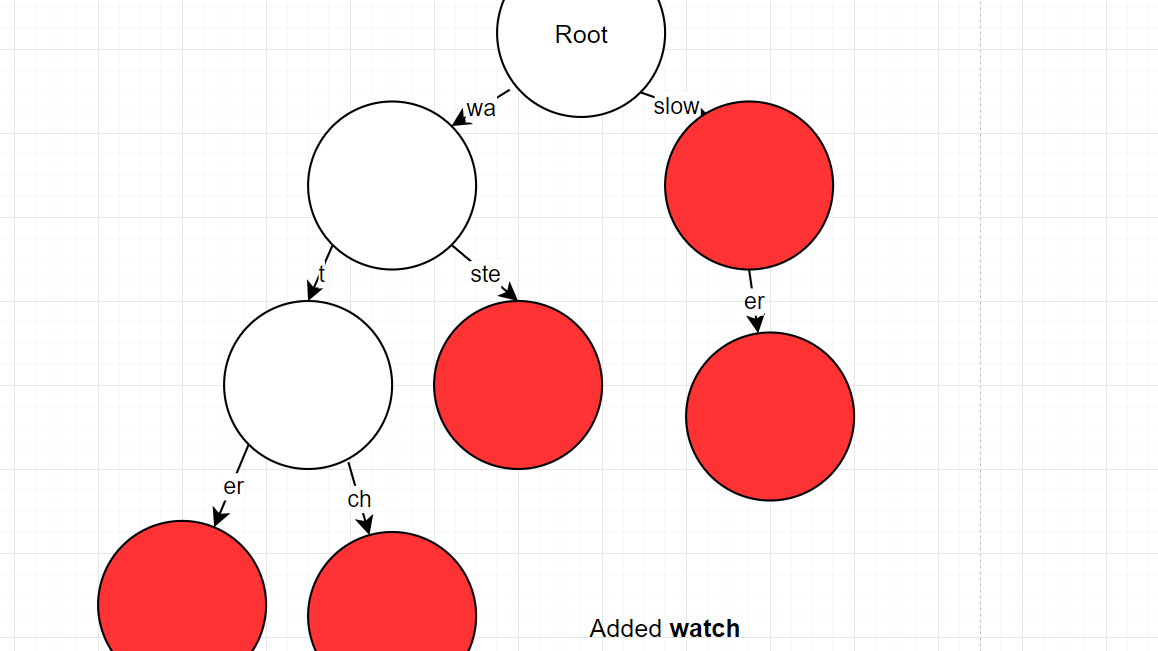
• Another case 3
• Process:
  • "watch" -> found "wa" as prefix, remove prefix from current input
  • "tch" -> found "ter" but misatch "te" != "tc"
    • "t" was previous matching prefix
    • must split "ter" into "t" and "er" and keep "er" property as a word.
  • "ch" -> normal insert

• Case 4
  • Prefix and the word fully match and both lengths are the same
  • Simply mark that node as a word node
• process:
  • "wa" -> found "wa", same length
  • mark node as word node.

Delete

Delete is a bit less troublesome than insert.
(This is was done recursively, but could be done iteratively but must keep track of the path taken)

1. Traverse your way down similar to searching.
   • If there is still are no edges with string input left or if the node is already a non-word node, then return.
2. Once at the correct node, mark it as a non-word node
   • if that node has no more edges and is not the root node then return null.
   • else return that correct node.
     Step 2 is the start of the back propagating phase where we return back to the root node and delete nodes when necessary to reduce memory costs and unncessary nodes
3. Check the returning node
   • if null, remove the edge that points to that null node.
     • if previous node has no edges due to removal and is non-word node, and is not root then return null
   • if only has 1 edge and is a non-word node
     • get that edge that the deleted node has.
     • delete the current edge from the current node to the returning node. But keep the string associated with this edge as it's going to be concatenated.
     • concatenate the saved string label with the returning node's edge string and assoicated with the returning node's edge next node.
   • else: return current node

Step 3 will be recursively done due to the recursive stacks unstacking

Code

For the following implementation, I've denoted word nodes as leaf nodes.
A hashmap is used to find the associated edge real quick based on the first letter.

private class Node { //This code is nested inside the RadixTree class
		private boolean isLeaf;
		private HashMap<Character, Edge> edges;

		public Node(boolean isLeaf) {
			this.isLeaf = isLeaf;
			edges = new HashMap<>();
		}

		public Edge getTransition(char transitionChar) {
			return edges.get(transitionChar);
		}

		public void addEdge(String label, Node next) {
			edges.put(label.charAt(0), new Edge(label, next));
		}
        
        public int totalEdges() {
			return edges.size();
		}
        
        public static void main(String[] args) {
            RadixTree radix = new RadixTree();
            radix.insert("test");
            radix.insert("water");
            radix.insert("slow");
            radix.insert("slower");
            radix.insert("team");
            radix.insert("tester");
            radix.insert("t");
            radix.insert("toast");

            System.out.println(radix.search("slower"));
            System.out.println(radix.search("t"));
            System.out.println(radix.search("te"));
            System.out.println(radix.search("tes"));
            System.out.println(radix.search("test"));
            System.out.println(radix.search("toast"));
            System.out.println(radix.search("tester"));

            radix.delete("test");
            radix.delete("t");
            radix.delete("slower");
            radix.delete("wate");

            System.out.println(radix.search("slower"));
            System.out.println(radix.search("t"));
            System.out.println(radix.search("te"));
            System.out.println(radix.search("tes"));
            System.out.println(radix.search("test"));
            System.out.println(radix.search("toast"));
            System.out.println(radix.search("tester"));

            radix.printAllWords();
	}
	}

There are three convenience methods to make the intent more obvious.

private class Edge { //This code is nested inside the RadixTree class
		private String label;
		private Node next;

		public Edge(String label) {
			this(label, new Node(true));
		}

		public Edge(String label, Node next) {
			this.label = label;
			this.next = next;
		}
}

This is the edge class where label is the string of characters.

import java.util.Collection;
import java.util.HashMap;

public class RadixTree {
	private static final int NO_MISMATCH = -1;
	private Node root;

	public RadixTree() {
		root = new Node(false);
	}
    
	private int getFirstMismatchLetter(String word, String edgeWord) {
		int LENGTH = Math.min(word.length(), edgeWord.length());
		for (int i = 1; i < LENGTH; i++) {
			if (word.charAt(i) != edgeWord.charAt(i)) {
				return i;
			}
		}
		return NO_MISMATCH;
	}
    
    //Helpful method to debug and to see all the words
    public void printAllWords() {
		printAllWords(root, "");
	}

	private void printAllWords(Node current, String result) {
		if (current.isLeaf) {
			System.out.println(result);
		}

		for (Edge edge : current.edges.values()) {
			printAllWords(edge.next, result + edge.label);
		}
	}

public void insert(String word) {
    Node current = root;
	int currIndex = 0;
    
    //Iterative approach
	while (currIndex < word.length()) {
        char transitionChar = word.charAt(currIndex);
		Edge currentEdge = current.getTransition(transitionChar);
        //Updated version of the input word
		String currStr = word.substring(currIndex); 

        //There is no associated edge with the first character of the current string
        //so simply add the rest of the string and finish
		if (currentEdge == null) {
			current.edges.put(transitionChar, new Edge(currStr));
			break;
		}

		int splitIndex = getFirstMismatchLetter(currStr, currentEdge.label);
		if (splitIndex == NO_MISMATCH) {
            //The edge and leftover string are the same length
            //so finish and update the next node as a word node
			if (currStr.length() == currentEdge.label.length()) {
				currentEdge.next.isLeaf = true;
				break;
			} else if (currStr.length() < currentEdge.label.length()) {
                //The leftover word is a prefix to the edge string, so split 
				String suffix = currentEdge.label.substring(currStr.length());
				currentEdge.label = currStr;
				Node newNext = new Node(true);
				Node afterNewNext = currentEdge.next;
				currentEdge.next = newNext;
				newNext.addEdge(suffix, afterNewNext);
				break;
			} else { //currStr.length() > currentEdge.label.length()
                //There is leftover string after a perfect match
				splitIndex = currentEdge.label.length();
			}
		} else {
            //The leftover string and edge string differed, so split at point
			String suffix = currentEdge.label.substring(splitIndex);
			currentEdge.label = currentEdge.label.substring(0, splitIndex);
			Node prevNext = currentEdge.next;
			currentEdge.next = new Node(false);
			currentEdge.next.addEdge(suffix, prevNext);
		}
        
        //Traverse the tree
		current = currentEdge.next;
		currIndex += splitIndex;
	}
}

The insert method handles all the cases mentioned in the insert section. It is performed iteratively but could be done recursively as practical situations wouldn't demand too many recursive stacks.

Worst case complexity: O(WordLength)

public void delete(String word) {
    root = delete(root, word);
}

private Node delete(Node current, String word) {
    //base case, all the characters have been matched from previous checks
    if (word.isEmpty()) { 
        //Has no other edges, 
		if (current.edges.isEmpty() && current != root) {
            return null;
		}
		current.isLeaf = false;
		return current;
	}

	char transitionChar = word.charAt(0);
	Edge edge = current.getTransition(transitionChar);
    //Has no edge for the current word or the word doesn't exist 
	if (edge == null || !word.startsWith(edge.label)) { 
		return current;
	}

	Node deleted = delete(edge.next, word.substring(edge.label.length()));
	if (deleted == null) {
		current.edges.remove(transitionChar);
		if (current.totalEdges() == 0 && !current.isLeaf && current != root) {
			return null;
		}
	} else if (deleted.totalEdges() == 1 && !deleted.isLeaf) {
			current.edges.remove(transitionChar);
			for (Edge afterDeleted : deleted.edges.values()) {
				current.addEdge(edge.label + afterDeleted.label, afterDeleted.next);
			}
		}
		return current;
	}

Traversing the string recursively similar to the manner of insert and search, but on the way back we make the necessary deletes.
Worst case complexity: O(WordLength)

public boolean search(String word) {
    Node current = root;
	int currIndex = 0;
	while (currIndex < word.length()) {
		char transitionChar = word.charAt(currIndex);
		Edge edge = current.getTransition(transitionChar);
		if (edge == null) {
			return false;
		}

		String currSubstring = word.substring(currIndex);
		if (!currSubstring.startsWith(edge.label)) {
			return false;
		}
		currIndex += edge.label.length();
		current = edge.next;
	}

	return current.isLeaf;
}

Basically traverse the tree and make sure all the characters match and that end node is a leaf to ensure it's a word.
Worst case complexity: O(WordLength)

Helpful

If you want a visual representation but with slightly different representation then I highly recommend trying out this link.
https://www.cs.usfca.edu/~galles/visualization/RadixTree.html

References

• https://en.wikipedia.org/wiki/Radix_tree
• https://iq.opengenus.org/tries/