A count min sketch data structure is a probabilistic data sturcture (a data structure that provides an approximate solution) that keeps track of frequency. In other words, the data structure keeps track of how many times a specific object has appeared.

Why use it?

The most common solution to the problem of keeping track of frequency is using a hash map.

If you don't know what a hash map is, I suggest you read up about it using OpenGenus's Hash Map article: Hash Map

However, there are two main issues using a hash map for this problem.

1. Collision issue
   • Often times a hash map will have to dynamically grow it's number of buckets/internal storage to hold all the data.
     • This means that there is a chance for a collision to happen and this would mean equality checks would be needed to find the key. Thus the performance is slower.
2. Memory issue
   • Another issue is that a hash map can be memory intensive and could be a problem if you want to not use too much memory. When you have over a million unique objects then that could become quite memory intensive as keeping a reference takes requires memory along with the contents within the object itself takes memory.

So how does count min sketch solve the problems of a hash map?
A count min sketch data structure is an alternative approach that can save memory while keeping high performance at the cost of accuracy.

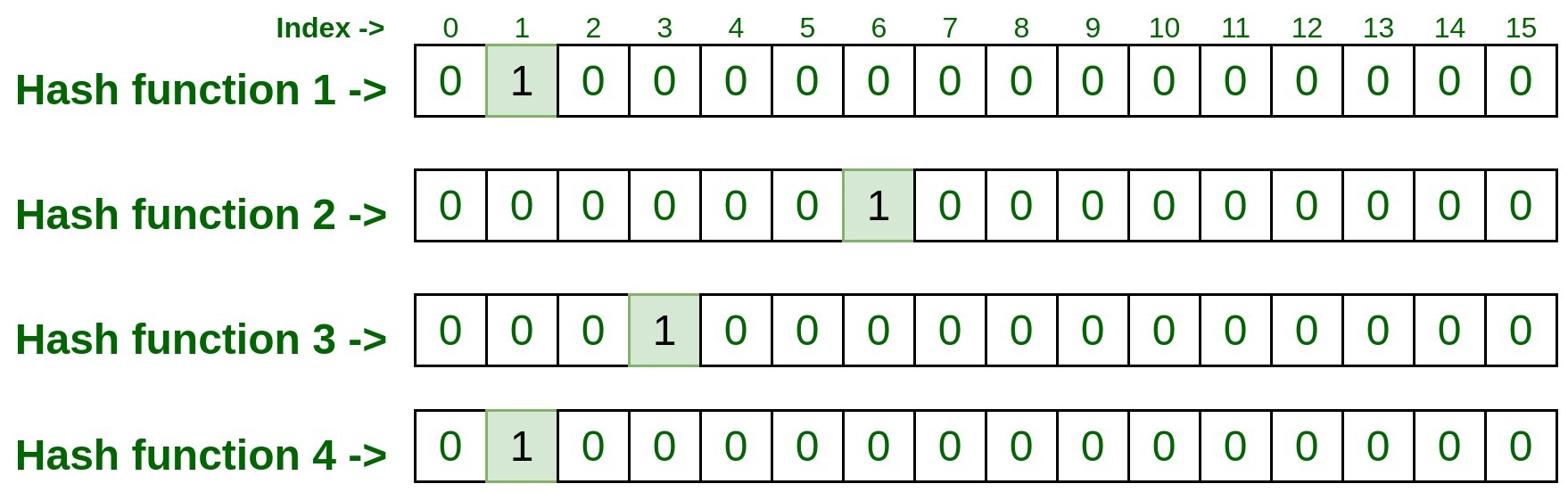
This image shows a representation of what the data structure tries to do, which is creating rows of width (w) number of buckets along an associated hash function for each row. The number of rows are determined by the number of hash functions, so technically yes you could only have 1 hash function but the more you have the more likely you will be more accurate (as long as the buckets are reasonable). And the width of each row (number of buckets) is up to the testing. There is no magic number but you can guarantee good results if there are more buckets than possible values but that defeats the purpose of saving memory, so you should aim for a number less than the total number of values through testing different widths.

A count min sketch uses the idea of a hash function and buckets to keep count but uses multiple hash functions and rows of buckets to figure out the count. Using a count min sketch will always result in an overestimate of the true count, so you will never get an underestimate of the true count.

• For example: a number may have only appeared 5 times but due to collisions it may be 10 times. Or perhaps a number never appeared but will have a count greater than 0 due to the hash values corresponding to a bucket with a positive count value.

The idea behind this is that even if a collision happens, there are other rows to check and hope that there weren't many collisions either. With enough buckets and enough high quality hash functions then an exact value could potentially be found but there is a chance for an overestimate.

The count min sketch doesn not need to store a reference of the object nor keep the object around for later, it only needs to compute the hash value as the column index and update the count for that hash function row.

What's important to take note is that the more high quality hash functions you have and sufficient enough buckets then the better the accuracy will be. However, you also to play around with the number of buckets, too little buckets will cause collisions but too many buckets will cause a waste of space.

Now that you the fundamental idea behind this data structure, it's important to know the standard functions that come with this data structure.

Functions

The two major functionalities that a count min sketch implement are:
put/update and get/estimate

The two functions can have different names but these are the common names that appear in different code implementations. The follow functions are written in java.
These two functions should be included in the implemention section to be fully functional.

Put / Update

public void update(T item, int count) {
    for (int row = 0; row < depth; row++) {
        frequencyMatrix[row][boundHashCode(hashers[row].hash(item))] += count;
	}
}

The code fragment above is a method that takes the item that you want to give an associated count to. A count min data structure typically has multiple rows, so you would iterate through each row and use the hash function to find which bucket the count will be added to. There is a possibility that the hash function creates a value that is greater than the length of the row, so the hash code is bounded to the value of 0 to row length - 1.

Get / Estimate

public int estimate(T item) {
    int count = Integer.MAX_VALUE;
	for (int row = 0; row < depth; row++) {
        count = Math.min(count, frequencyMatrix[row][boundHashCode(hashers[row].hash(item))]);
    }
    return count;
}

Now because this is probabalistic and there is a chance for collision, we have to go through each row and find the corresponding bucket index that item would appear in and find the minimum amount. The reason why we want the minimum is because we can guarantee the position where it should be but not the value if there are collisions on a few rows. As the implementation of add will simple handle collisions by adding onto the current value at that bucket position, it's safe to check the other rows as it's extremely unlikely for two objects of different values to have the same hash values (assuming it's a good hash function) for each row.

Possible Implementation

The following is a possible implementation of how a count min sketch using java.

import java.util.HashMap;
import java.util.Random;

public class CountMinSketch<T> {
	public static interface Hasher<T> {
		public int hash(T obj);
	}

	private int depth;
	private int width;
	private Hasher<T>[] hashers;
	private int[][] frequencyMatrix;

	@SafeVarargs
	public CountMinSketch(int width, Hasher<T>... hashers) {
		this.width = width;
		this.hashers = hashers;
		depth = hashers.length;
		frequencyMatrix = new int[depth][width];
	}

	public void update(T item, int count) {
        //implementation was shown in the section above
	}

	public int estimate(T item) {
		//implementation was shown in the section above
	}

    //Keep the hash code within 0 and length of row - 1.
	private int boundHashCode(int hashCode) {
		return hashCode % width;
	}

	public static void main(String[] args) {
        //Using functional programming to create these.
		CountMinSketch.Hasher<Integer> hasher1 = number -> number;
		CountMinSketch.Hasher<Integer> hasher2 = number -> {
			String strForm = String.valueOf(number);
			int hashVal = 0;
			for (int i = 0; i < strForm.length(); i++) {
				hashVal = strForm.charAt(i) + (31 * hashVal);
			}
			return hashVal;
		};
		CountMinSketch.Hasher<Integer> hasher3 = number -> {
			number ^= (number << 13);
			number ^= (number >> 17);
			number ^= (number << 5);
			return Math.abs(number);
		};
		CountMinSketch.Hasher<Integer> hasher4 = number -> String.valueOf(number).hashCode();

	int numberOfBuckets = 16;
		CountMinSketch<Integer> cms = new CountMinSketch<>(numberOfBuckets, hasher1, hasher2, hasher3, hasher4);
		Random rand = new Random();
        //Using a hashmap to keep track of the real count
		HashMap<Integer, Integer> freqCount = new HashMap<>();
		int maxIncrement = 10;
		int maxNumber = 1000;
		int iterations = 50;
        //add 50 random numbers with a count of 1-10
		for (int i = 0; i < iterations; i++) {
			int increment = rand.nextInt(maxIncrement) + 1;
			int number = rand.nextInt(maxNumber);

			freqCount.compute(number, (k, v) -> v == null ? increment : v + increment);
			cms.update(number, increment);
		}

        //Print out all the numbers that were added with their real and estimated count.
		for (Integer key : freqCount.keySet()) {
			System.out.println("For key: " + key + "\t real count: " + freqCount.get(key) + "\t estimated count: "
					+ cms.estimate(key));
		}
	}
}

Some important things to take note:

1. The update and estimate function implementations are in the sections above.
2. I've created a generic hasher interface and count min sketch data structure to allow flexbility in what values to hash. Though if you were working with strings or some primitive data type then you could simply change the types to suit what you want.
3. Inside the main function I've created 4 hash functions that deal with integers (they are not the best hash functions but can work) using functional programming.
4. Try to play around with the number of buckets, iterations, increment amount, and max number to get a better observations of the effects.
   • Also try removing a few of the hash functions and you will notice that the accuracy will decrease with less rows.
5. Lastly, there are other implementations out there that you can find that take into consideration of error.

Pros and Cons

Pros

• Very simple and easy to implement.
• Can minimize memory greatly and avoid equality checks.
• Customizable data structure to provide your own hash functions and the number of buckets.
• Can guarantee the value will be either be exact or an overestimate.

Cons

• A good chance the count is not exact, will probably be overestimate.
  • Such as a value never appeared once but will have a positive frequency count.
• Requires really good hash functions.
• Requires testing around to get the benefits of the data structure.

Other Applications

Besides being used for an alternative method of keeping track of a relative frequency count, there are other uses this data structure may be used in.

1. Possibly for a safe password picking mechanism.
   • passwords that are popular could be declined.
   • passwords that are extremely rare could have a high amount due to collisions which could also be declined.
   • This would mean passwords may need to be varied for this application.
2. In NLP (natural language processing), keeping frequency count on a large amount of data such as pairs / triplets can be reduced by using this data structure.
3. Heavily useful in queries too such as avoiding to go through the entire table of data and use approximate values to speed up queries.
   4) There are other applications such as: heavy hitters, approximate page rank, distinc count, K-mer counting in computational biology, and etc.

Resources

• https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6042851
• http://dimacs.rutgers.edu/~graham/pubs/papers/cmsoft.pdf
• https://easychair.org/publications/preprint_open/gNlw