Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes
In the field of Artificial Intelligence, neural networks have helped achieve so many breakthroughs with such great accuracy. There are many different types of neural networks that are used for specific purposes. For example, Convolutional Neural networks (CNN) are very useful when it comes to visual input analysis, Recurrent Neural networks (RNN) are quite useful in natural language processing etc. But when it comes to training these networks, there are certain problems that are present. As we keep on increasing the number of layers of networks, it becomes more and more difficult to train them.
It has been noticed that very deep networks shows increasing training error. This can be due to reasons such as problems in initialization of the network, optimization function, or due to one of the most famous problem i.e. vanishing gradient problem.
What is vanishing gradient problem?
It is a problem that is encountered while training artificial neural networks that involved gradient based learning and backpropagation. We know that in backpropagation, we use gradients to update the weights in a network. But sometimes what happens is that gradient becomes vanishingly small, effectively preventing the weights to change values. This leads to network to stop training as same values are propagated over and over again and no useful work is done.
To solve such problems, Residual neural networks are introduced.
What is ResNet?
Residual neural networks or commonly known as ResNets are the type of neural network that applies identity mapping. What this means is that the input to some layer is passed directly or as a shortcut to some other layer. Consider the below image that shows basic residual block:
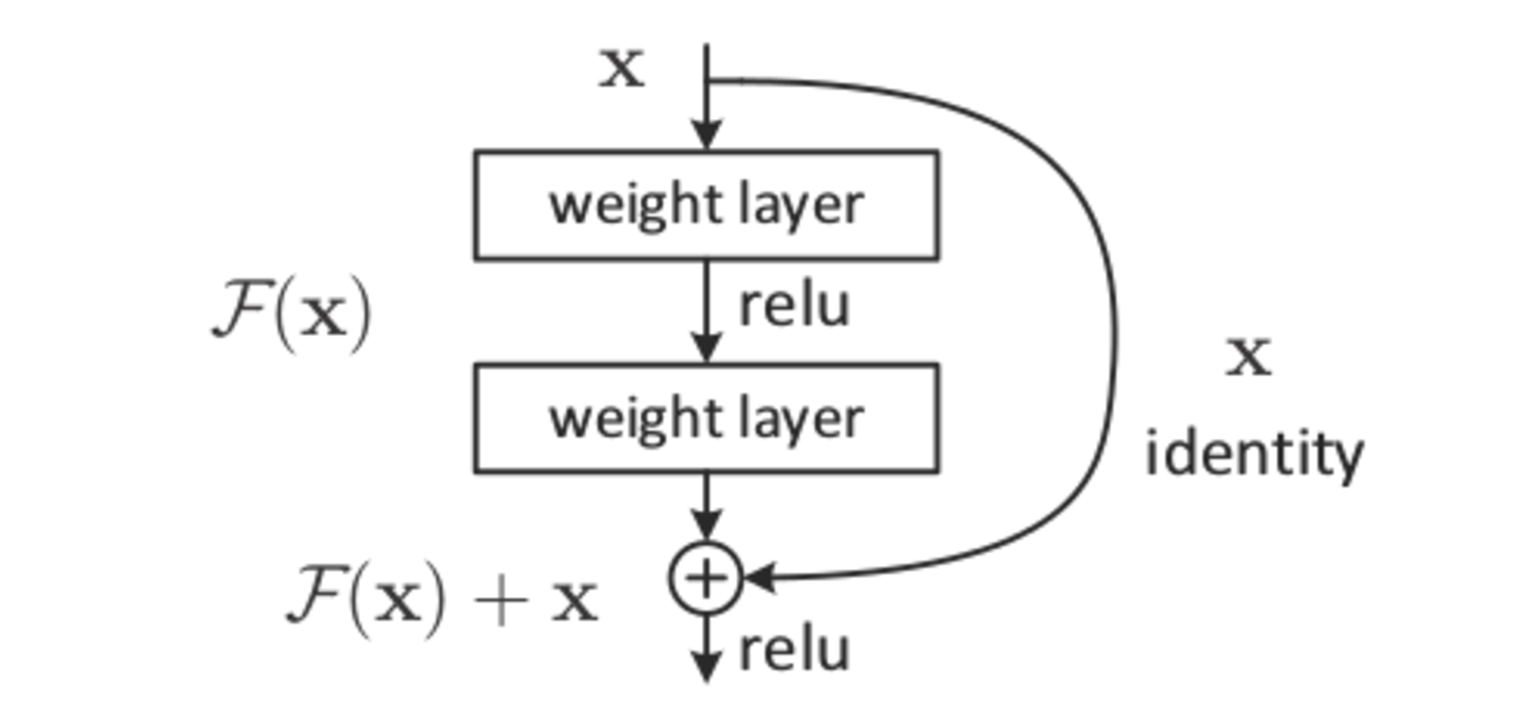
From the above figure, we can see that the most important concept involved here is the skip connection or the shortcut.
Skip connection is basically the identity mapping where the input from previous layer is added directly to the output of the other layer. From the above figure a basic residual function can be summarized as follows:
If x is the input and F(x) is the output from the layer, then the output of the residual block can be given as:
Y = F(x) + x
This is the most basic definition of a residual block.
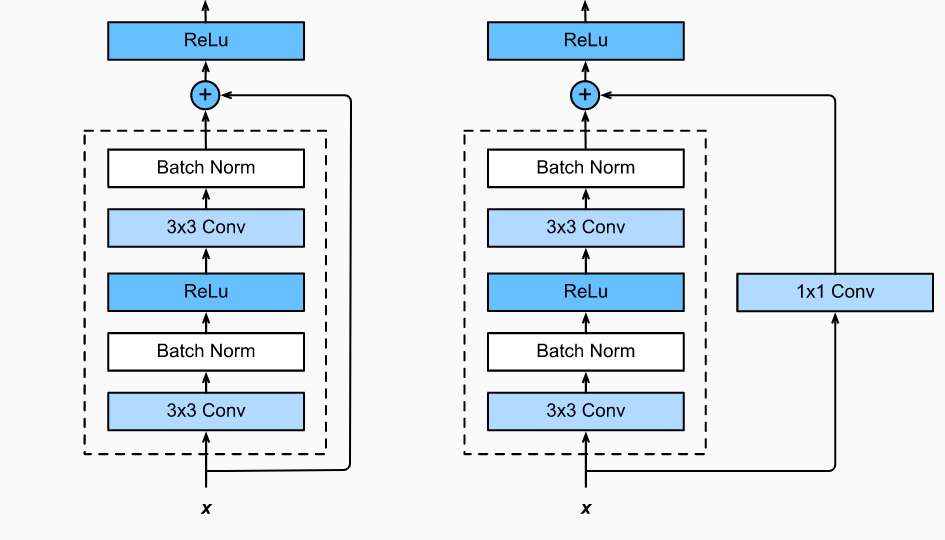
Now, there can be some scenarios where the output from the layer and the identity input have different dimensions. For example, if we consider a CNN where we know that after convolution operation, the size of the input is reduced(dimensionally), then adding input to it is a problem. So, what here can be done is that in the skip connection, we add some operation or function (in this example convolution operation) such that the input is changed or configured to the required dimensions.
So, the definition can be updated here as follows:
Y = F(x,{Wi}) + Ws*x
Here, Wi are the parameters given to the CNN layer and Ws term can be implemented with certain convolution configuration to make dimensions of input and output identical.
The following figure shows this concept:
With the help of ResNets, highly complex networks with around 1000 layers can be trained.
ResNet 18
ResNet-18 is a convolutional neural network that is trained on more than a million images from the ImageNet database. There are 18 layers present in its architecture. It is very useful and efficient in image classification and can classify images into 1000 object categories. The network has an image input size of 224x224.
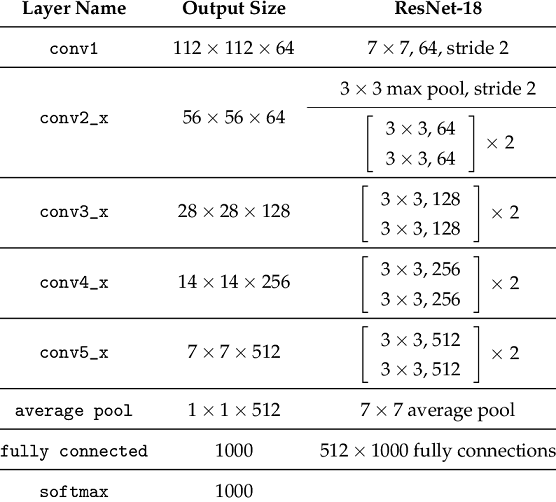
Consider the above diagram. From this diagram we can see how layers are configured in the ResNet-18 architecture. First there is a convolution layer with 7x7 kernel size and stride 2. After this there is the beginning of the skip connection. The input from here is added to the output that is achieved by 3x3 max pool layer and two convolution layers with kernel size 3x3, 64 kernels each. This was the first residual block.
Then from here, the output of this residual block is added to the output of two convolution layers with kernel size 3x3 and 128 such filters. This constituted the second residual block. Then the third residual block involves the output of the second block through skip connection and the output of two convolution layers with filter size 3x3 and 256 such filters. The fourth and final residual block involves output of third block through skip connections and output of two convolution layers with same filter size of 3x3 and 512 such filters.
Finally, average pooling is applied on the output of the final residual block and received feature map is given to the fully connected layers followed by softmax function to receive the final output. The output of each layer is shown in the diagram and input is changed in the skip connections according to that.
Now there are many variants of ResNets that have been introduced. Two of the popular ones are ResNext and DenseNet.
ResNext
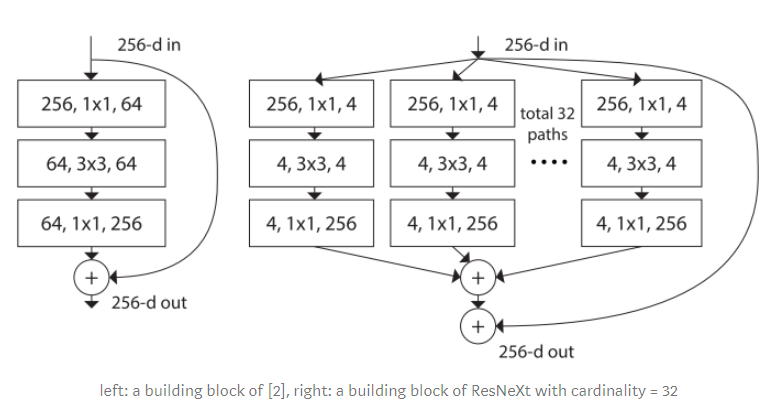
In this variant of ResNet, the concept that was introduced is that in a basic residual block, we add the input to output of the layer. Here what we do is that instead of output from just one layer, the output of several layers is concatenated and then the input is added to it.
The basic building block of ResNext can be shown as:
Here cardinality of the block is introduced. Cardinality is the number of independent paths that are concatenated (in the above figure, cardinality=32).
DenseNet
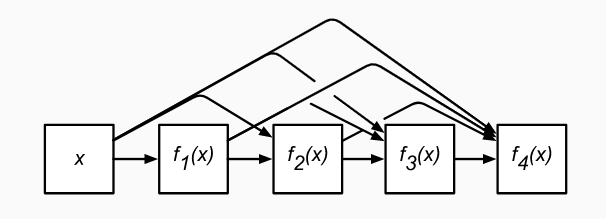
Densely Connected networks or DenseNet is the type of network that involves the use of skip connections in a different manner. Here all the layers are connected to each other using identity mapping. Consider the following basic block of DenseNet:
So, from the above diagram, we can see that the input from each layer is not only given to the next layer but is given to each subsequent layer.
Advantages of ResNet
- Networks with large number (even thousands) of layers can be trained easily without increasing the training error percentage.
- ResNets help in tackling the vanishing gradient problem using identity mapping.
Conclusion
To summarize, we can say that skip connection introduced in ResNet architecture have helped a lot to increase the performance of the neural network with large number of layers. ResNets are basically like different networks with slight modification. The architecture involves same functional steps like in CNN or others but an additional step is introduced to tackle with certain issues like vanishing gradient problem etc.