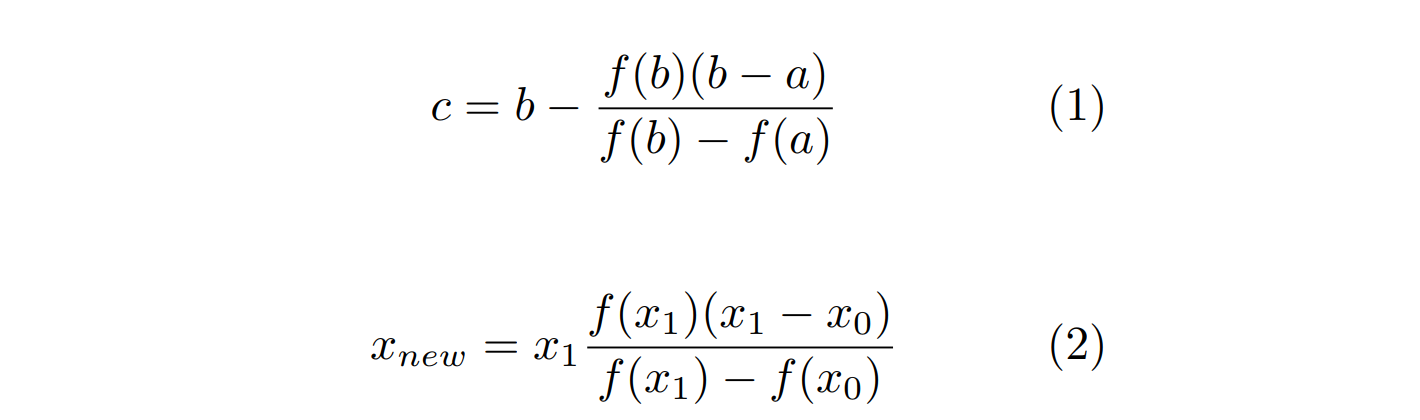Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 35 minutes | Coding time: 10 minutes
Secant Method is a numerical method for solving an equation in one unknown. It is quite similar to Regula falsi method algorithm. One drawback of Newton’s method is that it is necessary to evaluate f´(x) at various points, which may not be practical for some choices of f(x). The secant method avoids this issue by using a finite difference to approximate the derivative. As a result, root of f(x) is approximated by a secant line through two points on the graph of f(x), rather than a tangent line through one point on the graph.
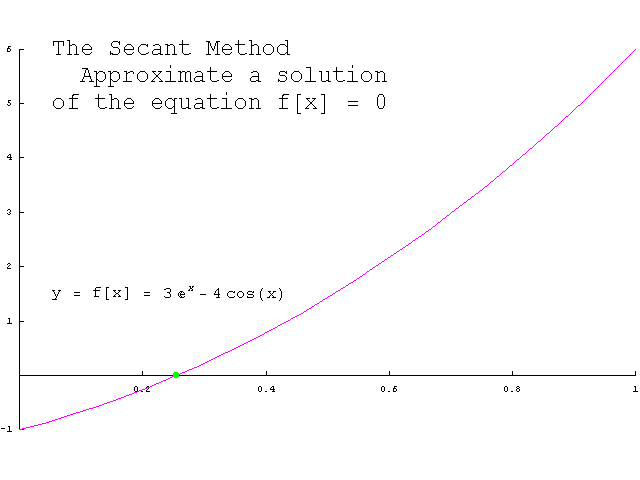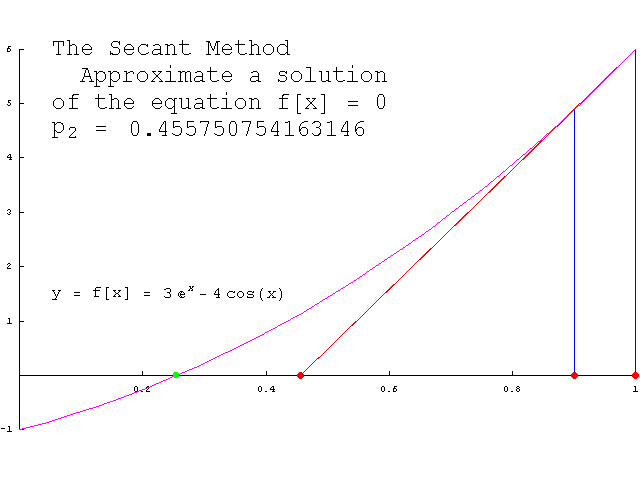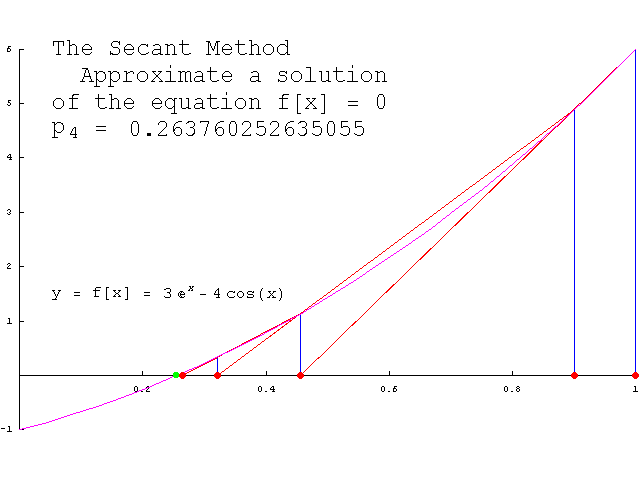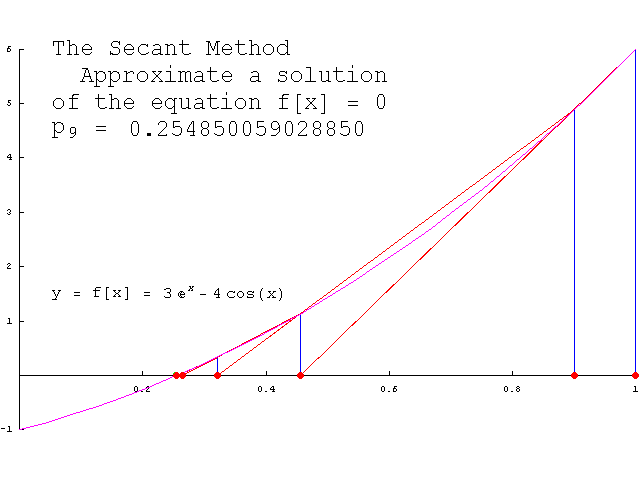
Theory
As stated above, in Secant method root of f(x) is approximated by a secant line through two points on the graph of f(x), rather than a tangent line through one point on the graph.
Since a secant line is defined using two points on the graph of f(x), as opposed to a tangent line that requires information at only one point on the graph, it is necessary to choose two initial iterates x0 and x1. Then, as in Newton’s method, the next iterate x2 is then obtained by computing the x-value at which the secant line passing through the points (x0, f(x0)) and (x1, f(x1)) has a y-coordinate of zero. This yields the equation
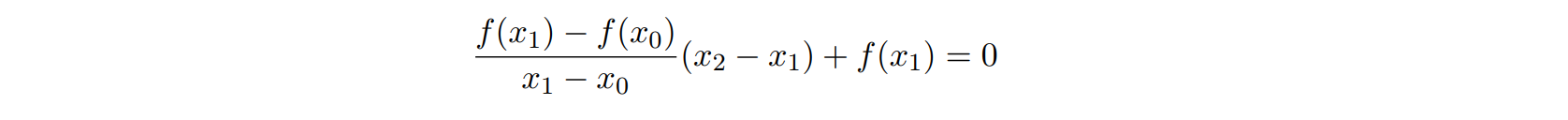
which gives x2 as :
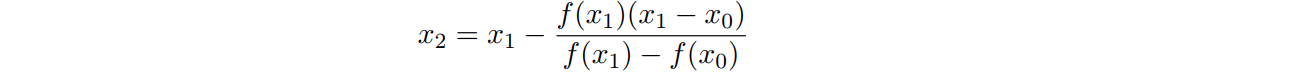
As you can see above that the equation for new estimate is same as in Regula falsi Mehtod but unlike in regula falsi method we don't check if the inital two estimates statisfy the condition that function sign at both points should be opposite.
Algorithm
For a given function f(x),the Secant Method algorithm works as follows:
1. Start
2. Define function f(x)
3. Input
a. initial guesses x0 and x1
b. tolerable error e
5. Do
x_new = x1 -(f(x1)*(x1-x0))/(f(x1)-f(x0))
x0 = x1
x1 = x_new
while (fabs(f(x_new)) > e) // fabs -> returns absolute value
6. Print root as x_new
7. Stop
Sample Problem
Now let's work with an example:
Find the root of f(x) = x3 + 3x - 5 using the Secant Method with initial guesses as x0 = 1 and x1 =2 which is accurate to at least within 10-6.
Now, the information required to perform the Secant Method is as follow:
- f(x) = x3 + 3x - 5,
- Initial Guess x0 = 1,
- Initial Guess x1 = 2,
- And tolerance e = 10-6
Below we show the iterative process described in the algortihm above and show the values in each iteration:
Inputs
f(x) = x3 + 3x - 5,
Initial Guess x0 = 1,
Initial Guess x1 = 2,
And tolerance e = 10-6
Iteration 1
x0 = 1, x1 = 2
-
We proceed to calculate x_new :
x_new = x1 -(f(x1) * (x1-x0))/(f(x1)-f(x0)) = 2 -(9 * (2-1))/(9-(-1))
x_new = 1.1 -
Now we update the x0 and x1
x0 = 2
x1 = 1.1 -
Check the loop condition i.e. fabs(f(x_new)) > e
f(x_new) = f(1.1) = -0.369
fabs(f(x_new)) = 0.369 > e = 10-6 ✅
The loop condition is true so we will perform the next iteration.
Iteration 2
x0 = 2, x1 = 1.1
-
We proceed to calculate x_new :
x_new = x1 -(f(x1) * (x1-x0))/(f(x1)-f(x0)) = 1.135446686
x_new = 1.135446686 -
Now we update the x0 and x1
x0 = 1.1
x1 = 1.135446686
Now we check the loop condition i.e. fabs(f(x_new)) > e
f(x_new) = -0.1297975921
fabs(f(_new)) = 0.1297975921 > e = 10-6 ✅
The loop condition is true so we will perform the next iteration.
As you can see, it converges to a solution which depends on the tolerance and number of iteration the algorithm performs.

C++ Implementation
#include <iostream>
#include <math.h>
#include<iomanip>
#include<chrono>
using namespace std::chrono;
using namespace std;
static double function(double x);
int main()
{
double x0;
double x1;
double x_new;
double precision;
cout << "function(x) = x^3 + 3x -5 "<<endl;
cout << "Enter initial guess x0: ";
cin >> x0;
cout << "\nEnter initial guess x1: ";
cin >> x1;
cout << "\nEnter precision of method: ";
cin >> precision;
int iter=0;
cout<<setw(3)<<"\niterations"<<setw(8)<<"x0"<<setw(16)<<"x1"<<setw(25)<<"function(x_new)"<<endl;
auto start = high_resolution_clock::now();
do{
x_new=x1-(function(x1)*(x1-x0))/(function(x1)-function(x0));
iter++;
cout<<setprecision(10)<<setw(3)<<iter<<setw(15)<<x0<<setw(15)<<x1<<setw(20)<<function(x_new)<<endl;
x0=x1;
x1=x_new;
}while(fabs(function(x_new))>=precision);//Terminating case
auto stop = high_resolution_clock::now();
auto duration = duration_cast<microseconds>(stop - start);
cout<<"\nRoot = "<<x_new;
cout<<"\nf(x)="<<function(x_new)<<endl;
cout << duration.count()<<" microseconds"<< endl;
return 0;
}
static double function(double x)
{
return pow(x,3) +3*x - 5 ;
}
More Examples

If you notice the examples used in this post are same as the examples in Regula Falsi Method but if you were to check number of iterations required you will notice Secant method being much faster than Regula falsi.
Limitations
Secant Method is faster when compared to Bisection and Regula Falsi methods as the order of convergence is higher in Secant Method. But there are some drawbacks too as follow:
- It may not converge.
- It is likely to have difficulty if f´(a) = 0. This means the x-axis is tangent to the graph of y = f(x) at x = a.
- Newton’s method generalizes more easily to new methods for solving simultaneous systems of nonlinear equations.
Question
If you look at the equation for new estimate in Regula Falsi Method and Secant method as follow :