
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 35 minutes | Coding time: 10 minutes
Newton's Method, also known as Newton-Raphson method, named after Isaac Newton and Joseph Raphson, is a popular iterative method to find a good approximation for the root of a real-valued function f(x) = 0. It uses the idea that a continuous and differentiable function can be approximated by a straight line tangent to it.
Theory
For a continous and differentiable function f(x), let x0 be a good approximation for root r and let r = x0 + h. The number h measures how far is x0 is from true root.
Since h = r - x0 is small we can use tangent line approximation as follow:
0 = f(r) = f(x0 + h) ≈ f(x0) + hf´(x0)
And unless hf´(x0) is close to zero we have,
h ≈ - f(x0) / f´(x0)
So this gives us the root r as,
r = x0 + h ≈ x0 - f(x0) / f´(x0)
Now we put x1 = x0 + h, where x1 is our new improved estimate, and we get the following equation
x1 = x0 - f(x0) / f´(x0)
The next estimate x2 is obtained from x1 in exactly the same way as x1 was obtained from x0:
x2 = x1 - f(x1) / f´(x1)
So we continue in this way, If xn is the current estimate, then the next estimate xn+1 is given by :
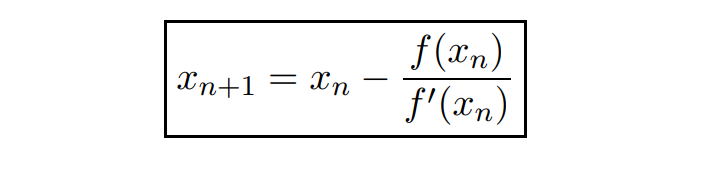
We can see graphically how Newton's Method works as follow:

Source: Openstax
We draw a tangent line to the graph of function f(x) at point x = x0. This tangent will have the equation as y= f´(x0)(x - x0) + f(x0). Now, we find the x intercept of this tangent by putting y = 0. The new x that we find is the new estimate. This continues till we reach the root of the function.
Algorithm
For a given function f(x),the Newton Raphson Method algorithm works as follows:
1. Start
2. Define function as f(x)
3. Define derivative of function as g(x)
4. Input:
a. Initial guess x0
b. Tolerable Error e
c. Maximum Iteration N
5. Do
If g(x0) = 0
Print "Mathematical Error"
Stop
End If
x(i+1) = x(i) - f(x) / g(x)
step = step + 1
If step > N
Print "Not Convergent"
Stop
End If
While abs f(x1) > e
7. Print root as x(i+1)
8. Stop
Sample Problem
Now let's work with an example:
Find the root of function f(x) = x2 - 4x - 7 taking initial guess as x = 5 using the Newton's Method to determine an approximation to the root that is accurate to at least within 10-9.
Now, the information required to perform the Newton Raphson Method is as follow:
- f(x) = x2 - 4x - 7,
- Initial Guess x0 = 5,
- f´(x) = g(x) = 2x - 4,
- And tolerance e = 10-9
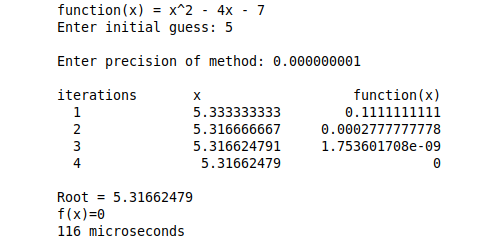
Below we show the iterative process described in the algortihm above and show the values in each iteration:
Inputs
- f(x) = x2 - 4x - 7,
- Initial Guess x0 = 5,
- And tolerance e = 10-9
We will calculate the f´(x) :
f´(x) = g(x) = 2x - 4,
Iteration 1
x0 = 5
f(x0) = f(5) = -2
- Check if g(x0) is not 0
g(x0) = g(5) = 2(5) - 4 = 6 which is not 0 ✅ - We then proceed to calculate x1 :
x1 = x0 - f(x0)/g(x0)
x1 = 5 - (-2/6) = 5.333333333
Now we check the loop condition i.e. fabs(f(x1)) > e
f(x1) = f(5.333333333) = 0.1111111111
fabs(f(c)) = 0.1111111111 > e = 10-9 ✅
The loop condition is true so we will perform the next iteration.
Iteration 2
x1 = 5.333333333
f(x1) = f(5.333333333) = 0.1111111111
- Check if g(x1) is not 0
g(x1) = g(5.333333333) = 2(5.333333333) - 4 = 6.666666666 which is not 0 ✅ - We then proceed to calculate x2 :
x2 = x1 - f(x1)/g(x1)
x1 = 5.333333333 - (0.1111111111/6) = 5.316666667
Now we check the loop condition i.e. fabs(f(x1)) > e
f(x2) = f(5.316666667) = 0.0002777777778
fabs(f(x2)) = 0.0002777777778 > e = 10-9 ✅
The loop condition is true so we will perform the next iteration.
As you can see, it converges to a solution which depends on the tolerance and number of iteration the algorithm performs.
C++ Implementation
#include <iostream>
#include <math.h>
#include<iomanip>
#include<chrono>
using namespace std::chrono;
using namespace std;
int N= 1000; // max iterations
static double function(double x);
double derivFunc(double x);
void newtonRaphson( double x, double precision);
int main() {
double x0;
double c;
double precision;
cout << "function(x) = x^2 - 4x - 7 "<<endl;
cout << "Enter initial guess: ";
cin >> x0;
cout << "\nEnter precision of method: ";
cin >> precision;
newtonRaphson(x0,precision);
return 0;
}
static double function(double x) // f(x)
{
return pow(x,2) - 4*x -7;
}
double derivFunc(double x) // f'(x) = g(x)
{
return 2*x - 4 ;
}
void newtonRaphson(double x, double precision)
{
int iter=0;
cout<<setw(3)<<"\niterations"<<setw(8)<<"x"<<setw(30)<<"function(x)"<<endl;
auto start = high_resolution_clock::now();
if(derivFunc(x)== 0 )
{
cout<<"Error";
return;
}
double h = function(x) / derivFunc(x);
do
{
h = function(x)/derivFunc(x);
// x(i+1) = x(i) - f(x) / f'(x)
x = x - h;
iter++;
cout<<setprecision(10)<<setw(3)<<iter<<setw(25)<<x<<setw(20)<<function(x)<<endl;
if (iter > N)
{
cout<<" Not Convergent";
break;
}
}while (fabs(function(x))>=precision);
auto stop = high_resolution_clock::now();
auto duration = duration_cast<microseconds>(stop - start);
cout<<"\nRoot = "<<x<<endl;
cout<<"f(x)="<<function(x)<<endl;
cout << duration.count()<<" microseconds"<< endl;
}
Limitations
Newton Raphson Method is one of the fastest method which converges to root quickly ( as it has quadratic convergence)
but there are also some drawbacks when this algorithm is used.
-
We need to calculate the derivative for the function we are performing the iterations for which adds in more computation than simple methods like Bisection or Regula Falsi method.
-
Since it is dependent on initial guess it may encounter a point where derivative may become zero and then not continue.
-
Newton's method may not work if there are points of inflection, local maxima or minima around initial guess or the root.
Let us see an examples below demonstrating the limitation
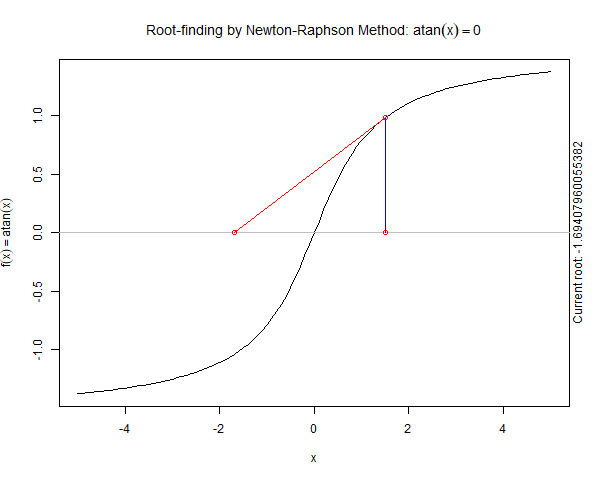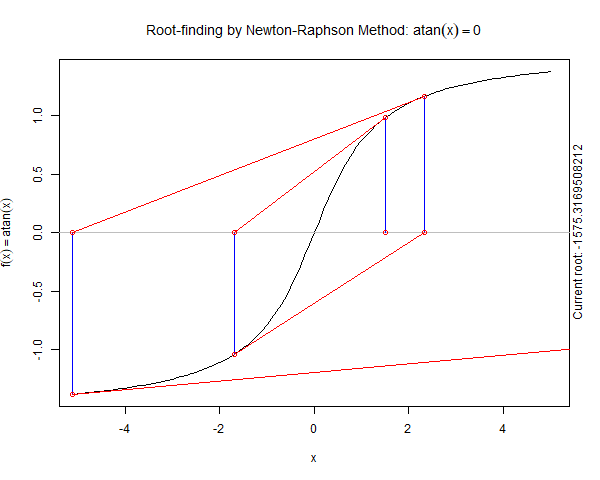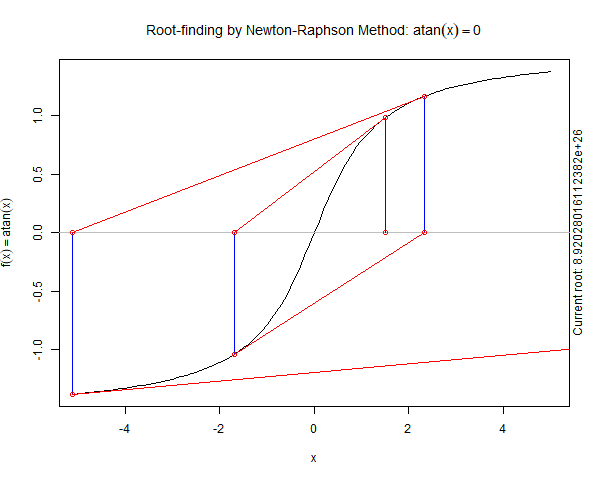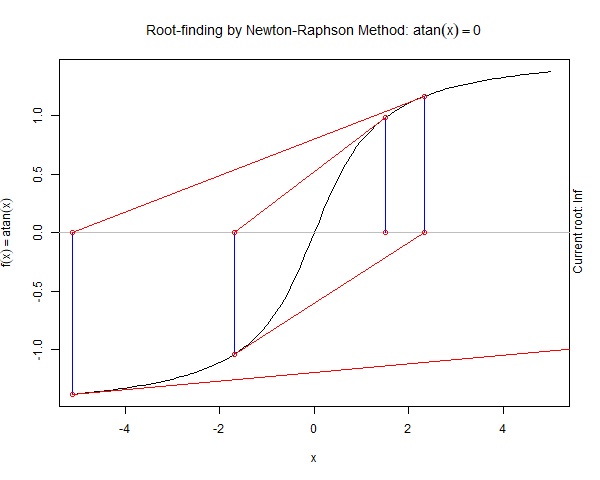
As we can see in the above graph the sequence of root estimates produces by Newton Raphson Method do not converge to the true root but rather osillate.
