
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 35 minutes | Coding time: 10 minutes
Regula Falsi method or the method of false position is a numerical method for solving an equation in one unknown. It is quite similar to bisection method algorithm and is one of the oldest approaches. It was developed because the bisection method converges at a fairly slow speed. In simple terms, the method is the trial and error technique of using test ("false") values for the variable and then adjusting the test value according to the outcome.
Theory
As before (in bisection method), for a given continuous function f(x) we assume that f (a) and f (b) have opposite signs ( a = lower guess, b = upper guess). This condition satisfies the Balzano's Theorem for continuous function.
Theorem (Bolzano) : If the function f(x) is continuous in [a, b] and f(a)f(b) < 0 (i.e. f(x) has opposite signs signs at a and b) then a value c ∈ (a, b) exists such that f(c) = 0.
Now after this bisection method used the midpoint of the interval [a, b] as the next iterate to converge towards the root of f(x).
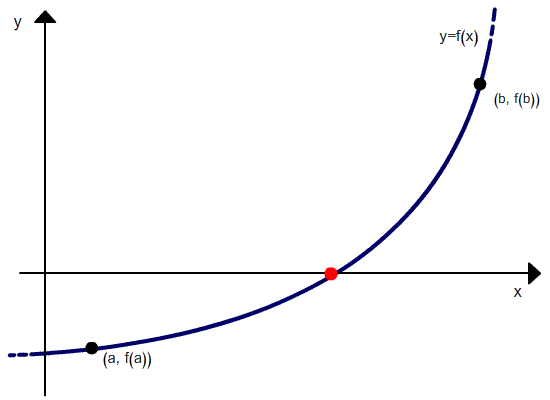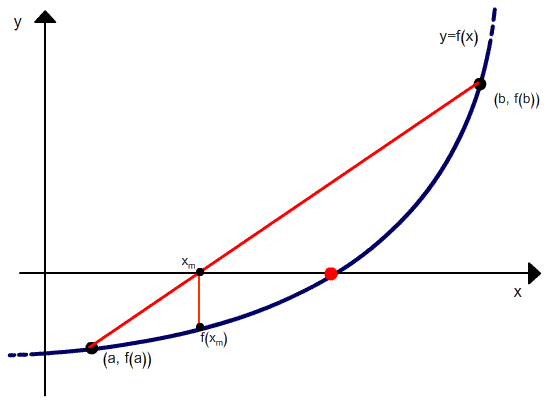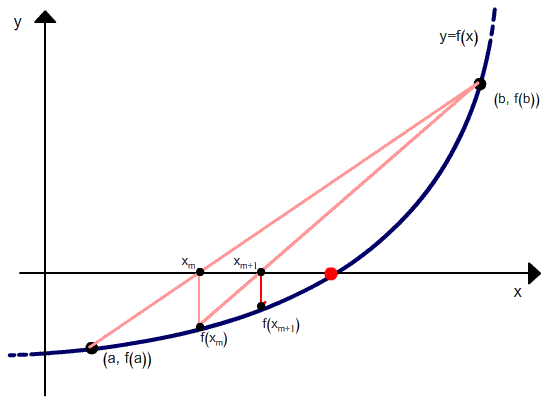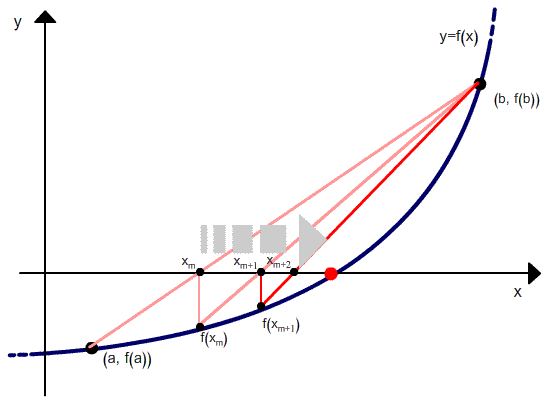
A better approximation is obtained if we find the point (c, 0) where the secant line L joining the points (a, f (a)) and (b, f (b)) crosses the x-axis (see the image below). To find the value c, we write down two versions of the slope m of the line L:
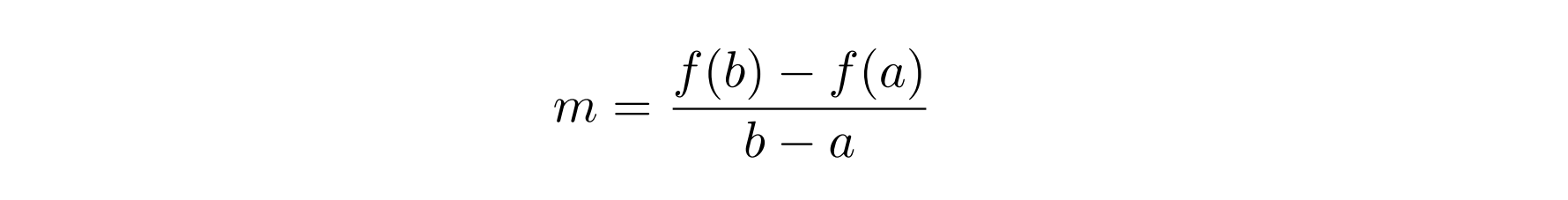
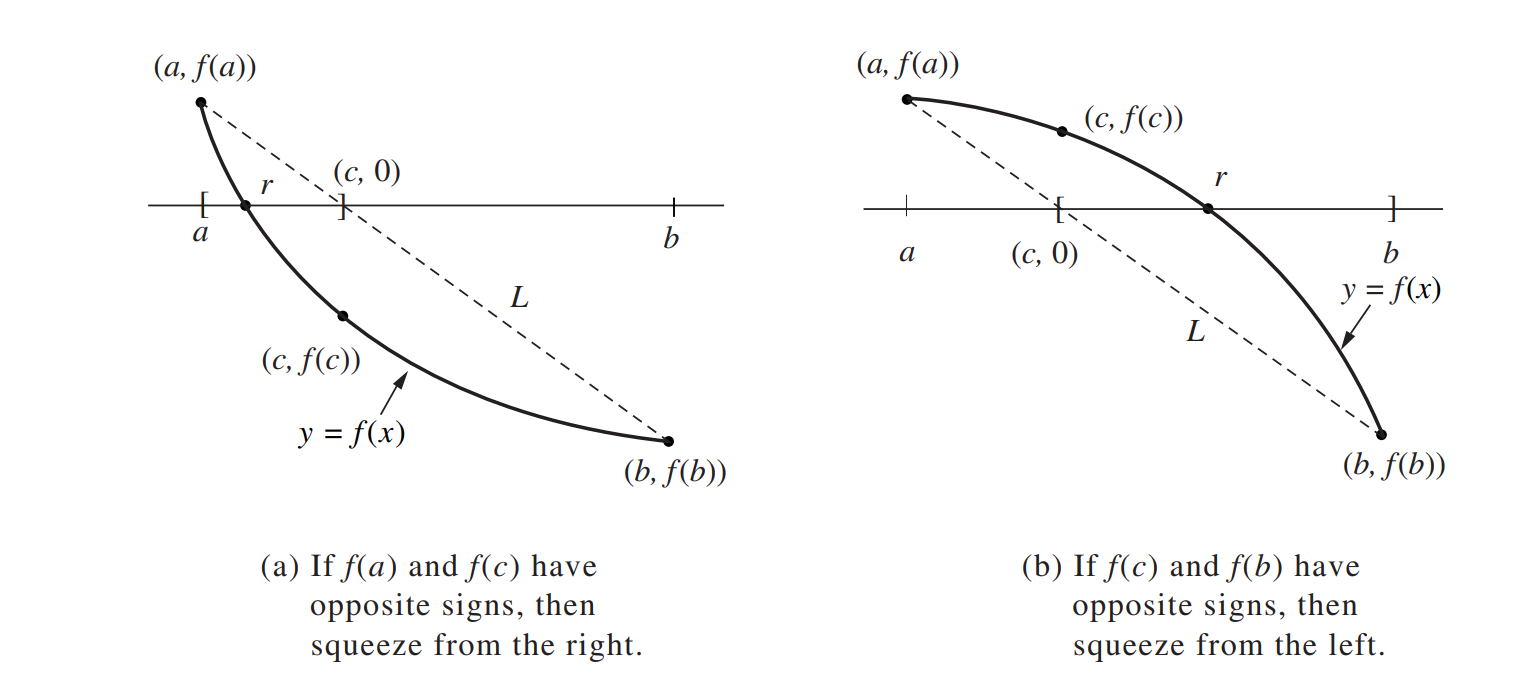
We first use points (a, f (a)) and (b, f (b)) to get equation 1 (below), and then use the points (c, 0) and (b, f (b)) to get equation 2 (below). Equating these two equation we get equation 3 (below) which is easily solved for c to get equation 4 (below):

The three possibilities are the same as before in the bisection method:
- If f (a) and f (c) have opposite signs, a zero lies in [a, c].
- If f (c) and f (b) have opposite signs, a zero lies in [c, b].
- If f (c) = 0, then the zero is c.
Algorithm
For a given function f(x),the Regula Falsi Method algorithm works as follows:
1. Start
2. Define function f(x)
3. Input
a. Lower and Upper guesses a and b
b. tolerable error e
4. If f(a)*f(b) > 0
print "Incorrect initial guesses"
goto 3
End If
5. Do
c = b -(f(b)*(b-a))/(f(b)-f(a))
If f(a)*f(c) < 0
b = c
Else
a = c
End If
while (fabs(f(c)) > e) // fabs -> returns absolute value
6. Print root as c
7. Stop
Sample Problem
Now let's work with an example:
Show that f(x) = x3 + 3x - 5 has a root in [1,2], and use the Regula Falsi Method to determine an approximation to the root that is accurate to at least within 10-6.
Now, the information required to perform the Regula Falsi Method is as follow:
- f(x) = x3 + 3x - 5,
- Lower Guess a = 1,
- Upper Guess b = 2,
- And tolerance e = 10-6
We know that f(a) = f(1) = -1 (negative) and f(b) = f(2) = 9 (positive) so the Intermediate Value Theorem ensures that the root of the function f(x) lies in the interval [1,2]
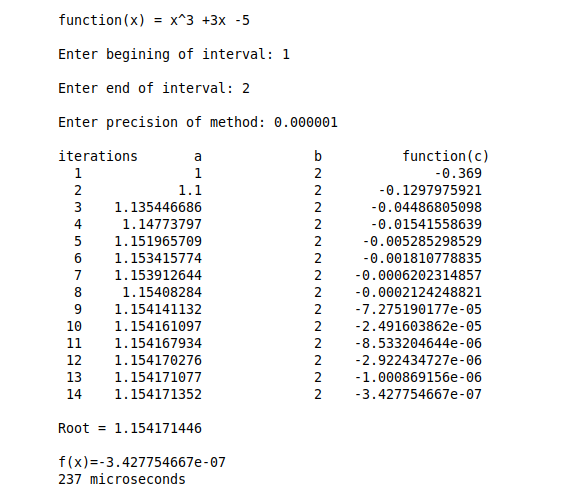
Below we show the iterative process described in the algortihm above and show the values in each iteration:
Inputs
f(x) = x3 + 3x - 5,
Lower Guess a = 1,
Upper Guess b = 2,
And tolerance e = 10-6
Iteration 1
a = 1, b = 2
-
Check if f(a) and f(b) have opposite signs
f(a) = f(1) = -1 ; f(b) = f(2) = 9
So, f(a) * f(b) = f(1) * f(2) = -9 < 0 ✅ -
We then proceed to calculate c :
c = b -(f(b) * (b-a))/(f(b) - f(a)) = 2 -(9 * (2-1))/(9-(-1))
c = 1.1 -
Check if f(a) and f(c) have opposite signs
f(a) = f(1) = -1 ; f(c) = f(1.1) = -0.369
f(a) * f(c) = f(1) * f(1.1) = 0.369 < 0 ❌
Since the above condition is not satisfied, we make c as our new lower guess i.e. a
a = c
a = 1.1
So, we have reduced the interval to :
[1,2] -> [1.1,2]
Now we check the loop condition i.e. fabs(f(c)) > e
f(c) = f(1.1) = -0.369
fabs(f(c)) = 0.369 > e = 10-6 ✅
The loop condition is true so we will perform the next iteration.
Iteration 2
a = 1.1, b = 2
- Check if f(a) and f(b) have opposite signs
f(a) = f(1) = -5 ; f(b) = f(1.5) = 2.375
So, f(a) * f(b) = f(1) * f(1.5) = -11.875 < 0 ✅
We then proceed to calculate c :
c = b -(f(b) * (b-a))/(f(b)-f(a)) = 1.135446686
c = 1.135446686
Check if f(a) and f(c) have opposite signs
f(a) = f(1) = -1 ; f(c) = f(1.135446686) = -0.1297975921
f(a) * f(c) = -0.1297975921 < 0 ❌
Since the above condition is not satisfied, we make c as our new lower guess i.e. a
a = c
a = 1.135446686
Again we have reduced the interval to :
[1,2] -> [1.135446686,2]
Now we check the loop condition i.e. fabs(f(c)) > e
f(c) = -0.1297975921
fabs(f(c)) = 0.1297975921 > e = 10-6 ✅
The loop condition is true so we will perform the next iteration.
As you can see, it converges to a solution which depends on the tolerance and number of iteration the algorithm performs.
C++ Implementation
#include <iostream>
#include <math.h>
#include<iomanip>
#include<chrono>
using namespace std::chrono;
using namespace std;
static double function(double x);
int main()
{
double a; // Lower Guess or beginning of interval
double b; // Upper Guess or end of interval
double c; // variable for midpoint
double precision;
cout << "function(x) = x^3 +3x -5 "<<endl;
cout << "Enter begining of interval: ";
cin >> a;
cout << "\nEnter end of interval: ";
cin >> b;
cout << "\nEnter precision of method: ";
cin >> precision;
// Check for opposite sign (Intermediate Value Theorem)
if (function(a) * function(b) > 0.0f)
{
cout<< "\nFunction has same signs at ends of interval";
return -1;
}
int iter=0;
cout<<setw(3)<<"\niterations"<<setw(8)<<"a"<<setw(16)<<"b"<<setw(25)<<"function(c)"<<endl;
auto start = high_resolution_clock::now();
// starting the iterative process
do{
c=a-(function(a)*(b-a))/(function(b)-function(a));
iter++;
cout<<setprecision(10)<<setw(3)<<iter<<setw(15)<<a<<setw(15)<<b<<setw(20)<<function(c)<<endl;
if((function(a)*function(c))<0)
b=c;
else
a=c;
}while(fabs(function(c))>=precision);//Terminating case
auto stop = high_resolution_clock::now();
auto duration = duration_cast<microseconds>(stop - start);
cout<<"\nRoot = "<<c;
cout<<"\n\nf(x)="<<function(c)<<endl;
cout << duration.count()<<" microseconds"<< endl;
return 0;
}
static double function(double x)
{
return pow(x,3) + 3*x -5 ;
}
More Examples

If you have seen the post on Bisection Method you would find this example used in the sample problem part. There the bisection method algorithm required 23 iterations to reach the terminating condition. Here we see that in only 12 iterations we reach the terminating condition and get the root approximation. So in this situation Regula Falsi method conveges faster than Bisection method.
But we cannot say that Regula Falsi Method is faster than Bisection Method since there are cases where Bisetion Method converges faster than Regula Falsi method as you can see below:


Limitations
While Regula Falsi Method like Bisection Method is always convergent, meaning that it is always leading towards a definite limit and relatively simple to understand but there are also some drawbacks when this algorithm is used. As both regula falsi and bisection method are similar there are some common limitaions both the algorithms have.
-
Rate of convergence
The convergence of the regula falsi method can be very slow in some cases(May converge slowly for functions with big curvatures) as explained above. -
Relies on sign changes
If a function f (x) is such that it just touches the x -axis for example say f(x) = x2 then it will not be able to find lower guess (a) such that f(a)*f(b) < 0 -
Cannot detect Multiple Roots
Like Bisection method, Regula Falsi Method fails to identify multiple different roots, which makes it less desirable to use compared to other methods that can identify multiple roots.
