Separate chaining collision resolution technique

In this article, we are going to see how we can actually resolve the collisions which happen during hash mapping using Separate chaining collision resolution technique.

Table of contents:

1. Introduction of Hash Table and Collisions
2. Separate chaining collision resolution technique
3. Example of Separate chaining collision resolution technique
4. Time and Space Complexity
5. Implementation of Separating Chaining resolution
6. Applications

Introduction of Hash Table and Collisions

As the name suggests, hash tables or hash maps use a mapping mechanism in which we map number or objects to be stored with slots in which they are going to be placed by using hash keys which can be derived using a carefully designed hashing function.

Searching for an element in a hash table can take as long as searching for an element in a linked-list time in the worst case in practice, however under reasonable assumptions hashing functions perform extremely well, as the average time to search for an element in a hash table is O(1), if hash keys don't collide(can also be called as direct address table).

Direct Address Table in the above diagram

In principle, to have O(1) search time complexity or O(1) insert time complexity or O(1) delete time complexity, we can have an array with size equal to the maximum element, where those elements will be stored at their respective keys(indices equal to that number)(also known as direct address table), but it may be possible we only have few numbers to store of which some are huge, which will lead to a lot of spaces to be unattended, which will make our program inefficient, and thus, we use a technique of mapping the number with a key called hash key, which corresponds to a slot in our hash table. To find the hash key of a number we use a carefully picked up hash function h(k), to compute the key which in turn will be used to store that number into its corresponding slot.

A basic problem arises while using hashing is , what if, two things or numbers to be stored have the same key, how can they be stored in the same slot, while maintaining the average efficiency which a direct address table provides?

Separate chaining collision resolution technique

The basic idea of Separate chaining collision resolution technique is:

• Each entry in a hash map is a Linked List
• If a collision happens, the element is added at the end of the Linked List of the respective hash.

On first sight, this might seem to give poor performance but on average, it works optimally and is used widely in practice. This is demonstrated in the Time and Space Complexity section of this article.

To solve this we use an array of pointers to keep track of the slots available for the storage(according to our choosen hash function) and those pointers are then made to point to the head of the linked list containing all those numbers or objects having the same key ,corresponding to that slot.

If two or more than two numbers point to the same slot or in other words have the same hash key as derived from the hashing function, then a linked list is formed with correspondingly indexed pointer pointing to the head of the linked list in which numbers will be stored forming a linked list.

And if, we again found a number which has hashing key equal to the slot which is not NULL or already has numbers present, then that number is simply inserted in the front forming a linked list, and repeating this process we can resolve the chaining issues in our hash table.

Example of Separate chaining collision resolution technique

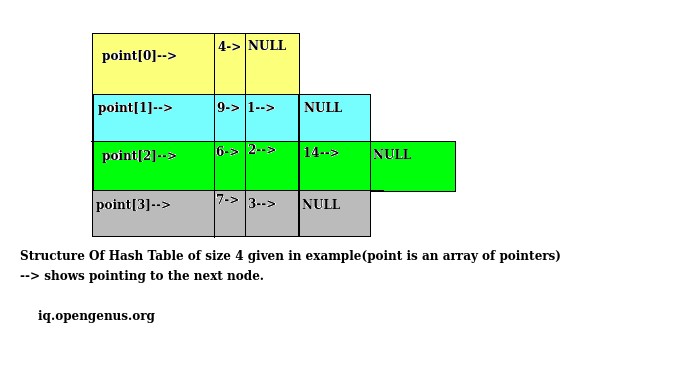
Suppose our hashing function h(k)= (Number mod 4).
And numbers to be stored are 14, 4, 3,2,1, 9,7, 6.

Calculated hash keys for various numbers:-
h(14)=2.
h(4) =0.
h(3) =3.
h(2) =2.
h(1) =1.
h(9) =1.
h(7) =3.
h(6) =2.

First while inserting 14, we got 2 as its key and hence, pointer indexed 2, will point to the structure having 14 as its data value.

After that similarly we can insert 4 and 3 at their corresponding slot.
When the time comes for the insertion of 2, since the slot is already filled, we make the pointer at index 2 to point to the structure having data value 2 and then, that structure's points to the structure having data value as 14, which, then points to NULL, as there is more node thereafter. Thus, creating a linked list with 2 nodes.

Continuing, we can simply insert 1 as its slot is empty which can be checked by checking the value of pointer indexed 1 which is NULL.
While inserting 9 whose key is 1 we again follow the chaining resolution technique by inserting 9 at the front of 1 thus, forming a linked list.

Similarly, we can do the insertion of 7 and 6.

Time and Space Complexity

Following is the Time and Space Complexity for

Complexity for insertion:-

Complexity for insertion is O(1), as it is same as inserting in the front of the linked list.

Complexity for searching:-

Worst case complexity for searching would be Θ(n), which will occur when all of the elements have same key, and thus, will then be similar to that of a linked list having n elements.

Best case time complexity for searching would be Θ(1), when each slot has only one element and thus, it will be similar to direct address table.

Average case time complexity:

Suppose, if there are n numbers to be stored with m slots available. Then, we define a load factor α for the hash table such that α=n/m, which can be less than, greater than or equal to 1 . Suppose the complexity of calculating key is constant.

Thus,
as n and m become proportional n/m approaches 1, and hence, average time complexity will be Θ(1), else it will be Θ(1+α), as every slot would have on an average n/m nodes which, would require us to search n/m elements and thus, the corresponding time complexity as mentioned before.

Complexity for deletion:-

Same as searching as for deletion to happen firstly searching is required, and since, once the node found, the time complexity for deleting that node will be Θ(1), thus, time will be consumed during the searching only durig the searching making its time complexity same as that of searching.

Implementation of Separating Chaining resolution

Code in C language showing separating chaining resolution is as follows:

#include<stdio.h>
#include<stdlib.h>

#define size 5

struct node
{
int data;
struct node *next;
};

struct node *point[size];

void make_pointers_NULL()
{
    int i;
    for(i = 0; i < size; i++)
        point[i] = NULL;
}
void insertion(int value)
{
    //Allocating memory for node.
    struct node *newNode = (struct node*)malloc(sizeof(struct node));
    newNode->data = value;
    newNode->next = NULL;



    //Calculating hash key using hash function.
    int key;
    key = value % size;

    //checking if point[key] is not pointing anywhere.
    if(point[key] == NULL)
    {    
        point[key] = newNode;
    }

    //Separate Collision resolution implementation.
    else
    {
        //Adding node at the front.
        struct node *temp = point[key];
        point[key]=newNode;

        newNode->next = temp;
    }
}

void print()
{
    int i;

    for(i = 0; i < size; i++)
    {
        struct node *temp = point[i];
        printf("point[%d]-->",i);
        while(temp)
        {
            printf("%d -->",temp->data);
            temp = temp->next;
        }
        printf("NULL\n");
    }
}

int main()
{
    //assigning every element of array of pointers to NULL.
    make_pointers_NULL();
    int i=0;
    while(i==0)
    {
        int value;
        scanf("%d",&value);
        insertion(value);
        printf("If you want to enter another value then enter 0 else
        enter 1");
        scanf("%d",&i);
    }

    print();

    return 0;
}

Applications

Hash tables are great for implementing dictionaries.They are used in compilers for keeping a track of all the identifiers declared by the user in the programming language. It can also be used in all those places where we need quick searching of some object, just by giving some information, like in database management system ,hash tables are used to keep track of huge chunk of data and to quickly serve the purpose of fequent searching, insertion or deletion at a rapid pace.