
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 12 minutes | Coding time: 9 minutes
The Shortest Path Faster Algorithm (SPFA) is an improvement of the Bellman–Ford algorithm which computes single-source shortest paths in a weighted directed graph. The algorithm is believed to work well on random sparse graphs and is particularly suitable for graphs that contain negative-weight edges.
The credit for SPFA algorithm goes to Fanding Duan.
The basic idea of SPFA is the same as Bellman–Ford algorithm in that each vertex is used as a candidate to relax its adjacent vertices. The improvement over the latter is that instead of trying all vertices blindly, SPFA maintains a queue of candidate vertices and adds a vertex to the queue only if that vertex is relaxed. This process repeats until no more vertex can be relaxed.
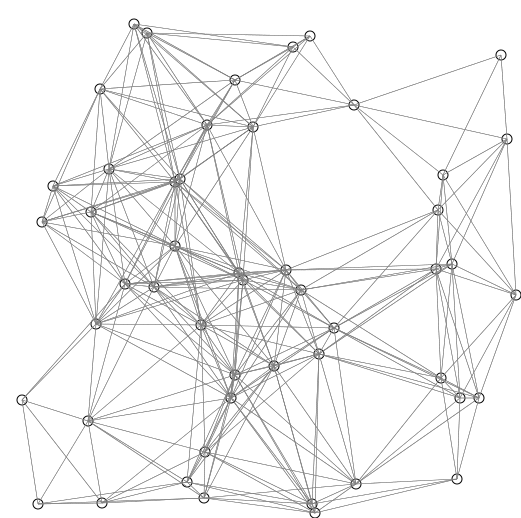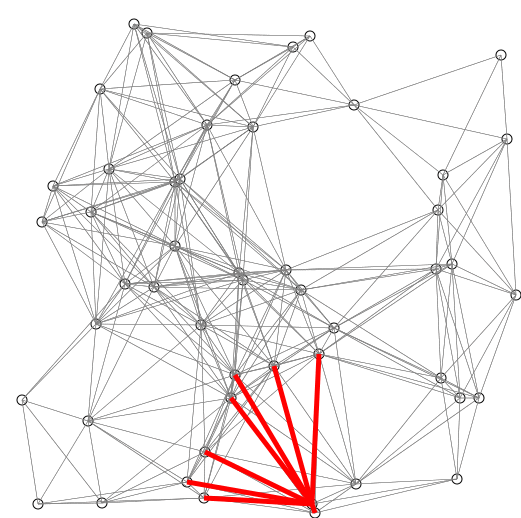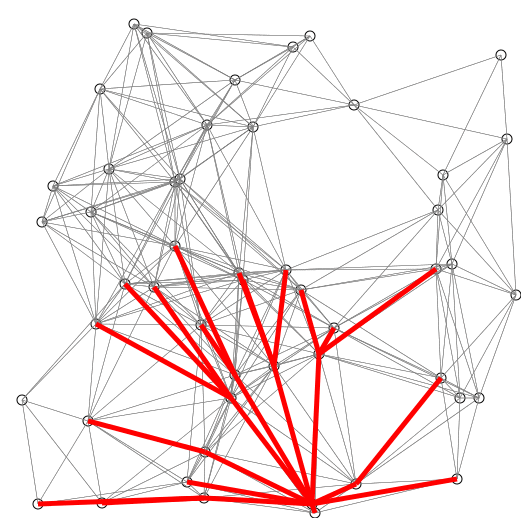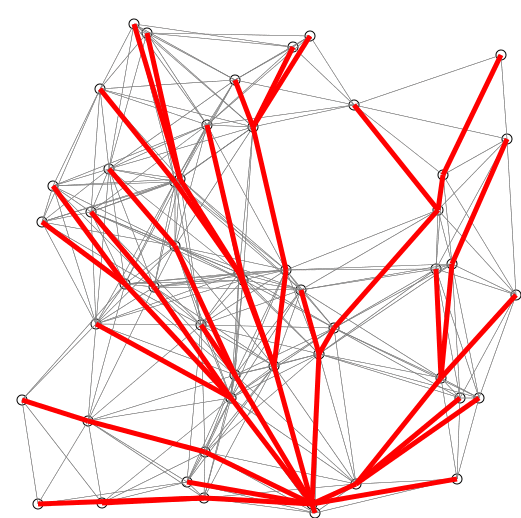
Visual: Red lines are the shortest path covering (so far observed). Blue lines indicate where relaxing happens, that is connecting v with a node u in Q, which gives a shorter path from the source to v.
The worst-case complexity of SPFA is the same as that of Bellman–Ford, so for graphs with nonnegative edge weights Dijkstra's algorithm is preferred.
The SPFA algorithm can be slow for certain data.
Suppose you want the shortest path from vertex 1 to vertex n, then we can add edge (i, i + 1) with a small random weight for 1 <= i < n (thus the shortest path should be 1-2-...-n) and randomly add 4n other heavy edges. For this case, the SPFA algorithm will be very slow compared to other shortest path algorithms.
Complexity
- Worst case time complexity:
Θ(VE) - Average case time complexity:
Unknown - Best case time complexity:
Unknown - Space complexity:
Θ(V)
Pseudocode
SPFA(v):
d[i] = inf for each vertex i
d[v] = 0
queue q
q.push(v)
while q is not empty
u = q.front()
q.pop()
for each i in adj[u]
if d[i] > d[u] + w(u,i)
then d[i] = d[u] + w(u,i)
if i is not in q
then q.push(i)
Applications
-
This algorithm is much faster than Bellman Ford algorithm for random sparse graphs.
-
It is much faster than the original Bellman-Ford, so it will be very helpful if we want to find the shortest path in graphs containing negative weight edges such as min cost flow problem.
