Sobel Filter/ Operator is a filter used in Convolution that is used to detect edges in an image. This is one of the fundamental approaches in Image Processing/ Machine Learning to detect edges.

Problem: You want to detect the edges in a large number of images with a program.

Background

How does a computer perform edge detection?

Edge detection is performed by looking for regions where there is a sharp change in colour or intensity.

An image can be transformed into a grid with numbers which indicate the colour of each pixel. These numbers range from 0 to 255 and usually a layer can be divided into Red, Green and Blue layers.

Edge detection is often employed in convolutional neural networks, more about which you can find here in an article Understanding Convolutional Networks through Image Classification.

Example - vertical line

This is an image with white on one side and black on the other - there is a vertical edge running down the middle of the square.

This can also be approximated as this grid, if we define white as "1" and black as "2":

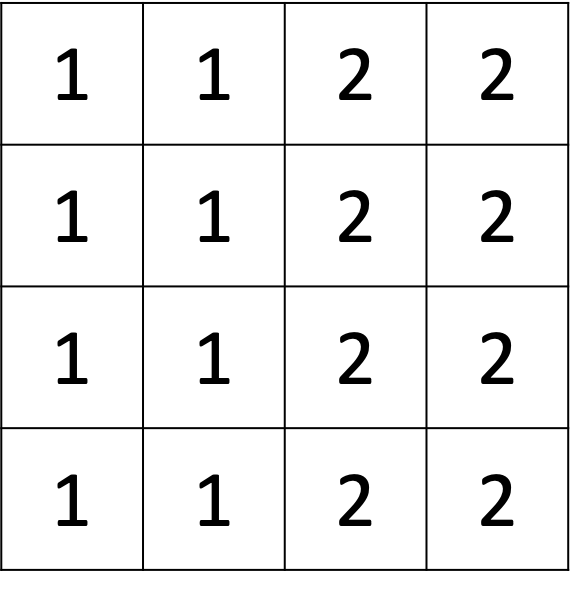
The vertical Sobel filter is

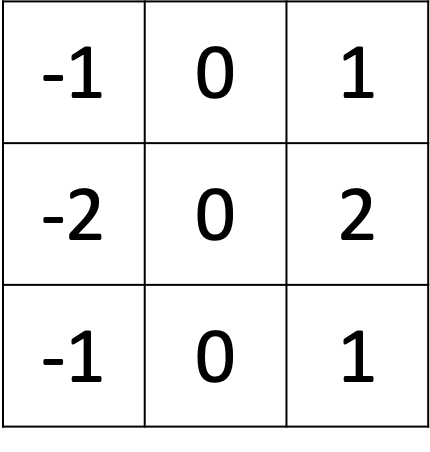
At the point (2,2), counting from the top left upper corner of the graph,

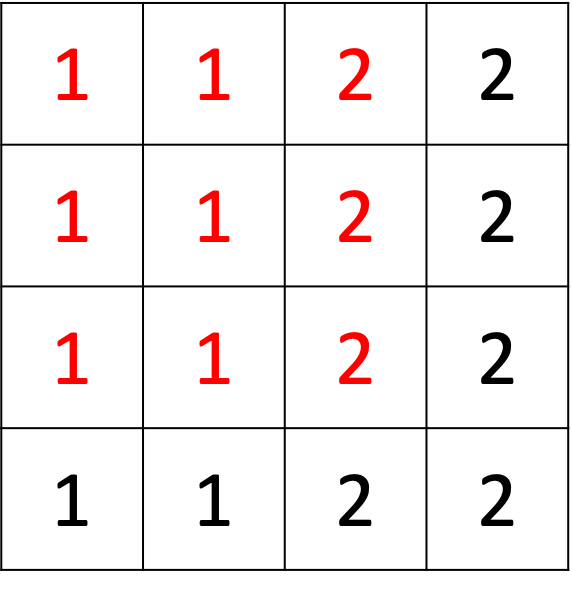
the value of the filter is (1+2+1) = 4, so that implies there is an edge.

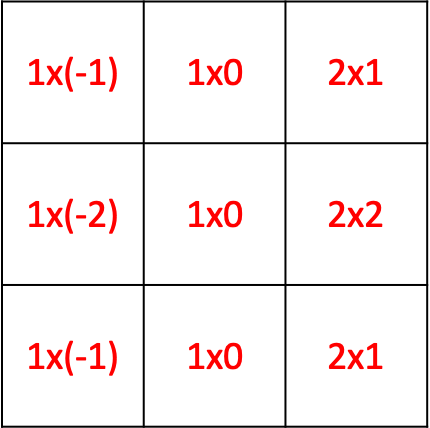
The horizontal filter is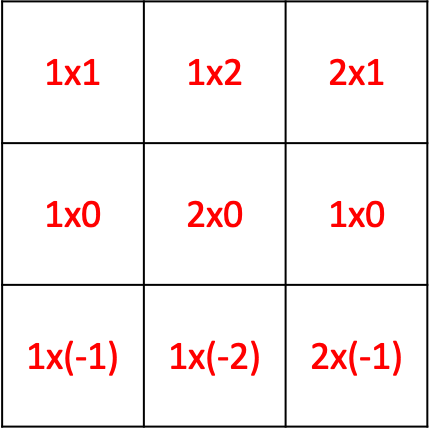
and calculated at the same point (2,2), the value of the filter is 0, so that implies there is no horizontal edge - which is true since there is only a vertical edge in this case.

What can the value signify?

The magnitude of the change
As a thought exercise, consider an image where the pixels on the image are defined as 100 and 200 instead of 10 and 20. What would the value be when we apply the vertical filter?

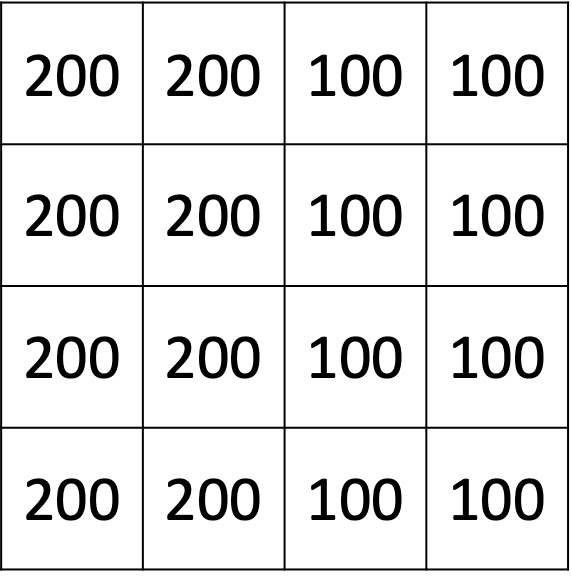
Following the above example, as the image defined with 1s and 2s yield 4, the image with 100 and 200s will return 400. This implies a more significant contrast between colours.

Whether the image goes from dark to light or the reverse
As another thought exercise, let us consider the image flipped horizontally, that is with black on the left side and white on the right. What would the value be when we apply the vertical filter?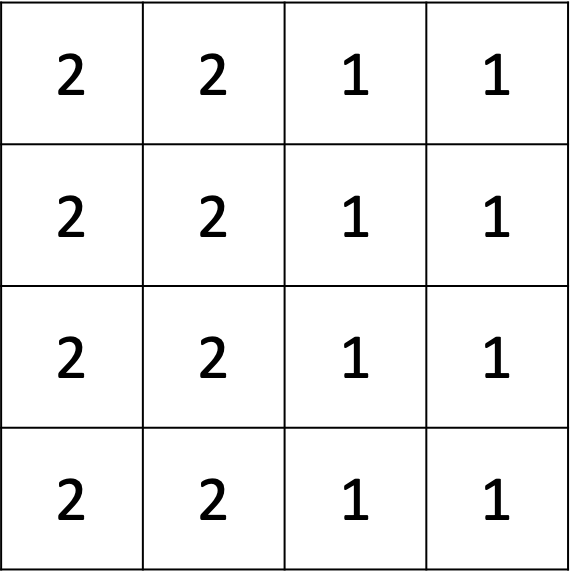
With the same logic, the point (2,2) should yield -4.

More about the vertical filter
A positive value means that the left side is lighter than the right side when using this filter. Of course by flipping the vertical filter horizontally, this changes the definition and so a positive value implies that the left side is darker than the right side when the filter is flipped. However the classic filter is given as such.

Modifying the filter
The filter can be further modified by changing the values from "2" to "20" for example - then the changes in values will also be more signficant.

Mini-Conclusion
A value, positive or negative, indicates that there is an edge. 0 means there is no edge (or in other words, that there is no change in the value of the pixel).

Application

This filter in fact allows us to approximate an image by defining its lines. In a Machine Learning Network to identify images, for instance questions like "is there a person in this figure", the network usually has several layers. In the earlier layers, lines and colours might be identified and only in the later layers when the computer has "learned" where the edges are will it start detecting entire objects. Hence edge detection is a crucial component in image detection using convolution networks.

Code

What does a single step of this convolution layer look like? Here this is demonstrated with Python tensorflow.

First the necessary libraries are imported as follows:

import numpy as np
import h5py
import matplotlib.pyplot as plt

Let's define a function, convolution, as a function that applies a filter, defined by the parameters W, on a single slice (slice) of the output activation of the previous layer.

Typically when implementing image detection, there are multiple channels (representing the number of filters) and these channels can be thought of as the "depth" of the layer. Hence each layer of the network usually has 3 components - the height, width and number of channels "depth".

Let C_prev be the number of channels in the previous layer and f be the size of the filter. In the previous case, we would have the number of channels = 1 and the filter be 3 x 3.

W are the weight parameters contained in a window which is a matrix of shape (f, f, n_C_prev) and a_slice_prev is a slice of input data with the shape (f, f, n_C_prev). b are the bias parameters in a window-matrix of shape (1, 1, 1). This should return Z, a scalar value, which is the result of convolving the sliding window (W, b) on a slice x of the input data.

There are three steps involved in the convolution, represented in a formula as (Z = Wa + b). First, perform an element-wise product using np.multiply between a_slice_prev and W. Then, sum over all the entries of this product. Finally, add the bias b to Z, with b being a float.

def convolution(slice, W, b):
    s = np.multiply(slice, W)
    Z = np.sum(s)
    Z = Z + float(b)
    return Z

This runs a single iteration of the convolution - to perform multiple iterations, loop over the number of images in the dataset, then the height, width and number of channels with a nested if loop.

For instance, with m training examples and height, width and number of channels as (H, W, C) respectively. Let the stride be the number of units from one filter to another (the default would be 1, e.g. moving from (2, 2, 1) to (3, 2, 1)) - the code would be as follows:

for i in range(len(m)):
     slice = Slice[i,...]
     for h in range(H):
         vert_start = h * stride
         vert_end = h * stride + f
            
            for w in range(len(W))):
                horiz_start = w * stride
                horiz_end = w * stride + f
                
                for c in range(len(C)):
                    current_slice = slice[vert_start:vert_end, horiz_start:horiz_end,:]
                    Z[i, h, w, c] = convolution(current_slice, W[:, :, :, c], b[:,:,:,c])

"Slice" is a large database with all the different training examples, the first for-loop selects the ith training example. The next two for-loops determine the height and width of the start and end points of the input figure to get "slice".

Then current_slice is determined from the ith slice with the height and width and finally, it is fed into the convolution function.

Conclusion

The Sobel filter is a type of filter to determine the edges in an image. It is typically implemented in a Convolutional Network as an activation layer and is a precursor for image identification.

With this article at OpenGenus, you must have the complete idea of using Sobel filter used for edge detection. Enjoy.