In this article, we have explored how to solve string matching problem (find all occurences of string S1 in another string S2) using Bitset. It is a modification of the naive approach which takes O(L x P x logL) time complexity and assumes all positions to be potential matches and eliminates them based on previous comparisons. The modification with bitset improves the time complexity to O(L x P / K) where L is length of string S2, P is length of string S1 and K is register size.

Bitset

Bitset is a fixed sized bit array in which every element is a single bit in the memory. Bitset supports all the bitwise operations that are applicable on primitive data types. The operations on bitset are optimally implemented in the libraries.

The operations on bitset has a complexity of O(N / K), where N is the length of the bitset and K is the register size of the system (generally 32 or 64).

Bitset also has other operations - set and reset, the former set's a bit to 1 and the latter set's a bit to 0. These operations take O(1) or constant time.

String matching

String-matching or string-searching is a process used to find the positions (or number of occurrences) in a text where a desired pattern occurs. This can be performed using various data-structures and algorithms. Examples: The prefix array (Knuth-Morris-Pratt algorithm), the trie based finite deterministic automaton (Aho-Corasick algorithm), Suffix automaton and Suffix Tree (Ukkonen's algorithm).

Naive string-matching

Consider the code for finding all occurrences of pattern in text.

int naiveStringMatching(string text, string pattern) {
  set<int> startPositions;
  for(int i = 0; i < text.size(); ++i) {
    startPositions.insert(i);
  }
  for(int j = 0; j < pattern.size(); ++j) {
    for(auto it = startPositions.begin(); it != positions.end(); ) {
      int pos = (*it);
      if((pos + j >= text.size()) || text[pos + j] != pattern[j]) {
        it = startPositions.erase(it);
      } else {
        ++it;
      }
    }
  }
  return startPositions.size();
}

The above algorithm is one of the naive algorithm's for finding all the occurrences of pattern in text.

This algorithm initally assumes that every position in the text is a potential starting position of a substring which is same as pattern . Iterating through the pattern at each iteration j, the algorithm removes a starting position pos if the character j steps away from it (text[pos + j]) is not the same as the character pattern[j]. Because the substring starting at pos cannot be the same as the pattern.

This algorithm has a worst case time complexity of O(|T| * |P| * log|T|) (|T| is the text length and |P| is the pattern length). Bitset can be used to remove the inner loop and make the algorithm much faster.

Optimized algorithm

String-matching using bitset is similar to the above naive approach with some pre-processing on text.

    const int N = MAX_LEN + 1;
    bitset<N> mask[26];
    void computeMask(string text) {
      text = "#" + text; // to make text it 1-indexed.
      for(int i = 1; i < text.size(); ++i) {
        int c = text[i] - 'a'; 
        mask[c].set(i); 
      }
    }

NOTE: Without loss of generality, it is assumed that the application consists of only lower case English letters.

The computeMask method performs the pre-processing on text. This method essentially creates 26 bitset's (each of length N - maximum length of text + 1), one for each letter in the alphabet. The i th bit in mask[c] is set to 1 only if text[i] is the cth character in the alphabet, otherwise it is 0. Therefore, mask[c] represents all the locations in text which has the character c.

The naive algorithm is optimized using mask.

int optimizedStringMatching(string pattern) {
  if(pattern.size() > text.size()) { return 0; } 
  pattern = "#" + pattern;
  bitset<N> startMask; 
  startMask.set(); // all bits are set to one
  for(int i = 1; i < pattern.size(); ++i) {
    int c = pattern[i] - 'a';
    startMask &= (mask[c] >> i);
  }
  return startMask.count(); // count() returns number of 1 bits
}

The startPositions in the naive approach is replaced with startMask, which consists of N bits - one for each position in text. Like in the naive algorithm, initially all the positions are considered to be potential starting positions and the inner loop (of the naive algorithm) is mimicked using 2 lines of code.

mask[c] >> i is the cth mask left-shifted i times, also c is the ith character in pattern. The left shift is performed to offset the character and overlap with the starting positions of the substring which could be same as pattern. In each iteration i bitwise and is performed between the left-shifted mask and startMask, this unsets all those positions if the character i characters away is not the same as pattern[i]. The unsetting part it done in one shot unlike the naive algorithm, making it much faster.

Complexity

The above algorithm has a complexity of O(|P| * (|T| / K)), where |P| is the length of the pattern string, and |T| is the length of the text string and K is the register size. This is because, for each character in |P| bitset (length is |T|) shifting and and is performed, whose cost is |T| / K.
The pre-processing time is O(|T|), as mask has to be set for each character in the text string.
Memory usage is O(A * |T|) bits, where A is the number of letters in the alphabet.

Other features of the algorithm

• Number (or positions) of occurences in a range of text can also be found as follows:

    string text;
    bitset<N> mask[26];
    bitset<N> startMask; 
    
    int rangePatternMatchCount(string pattern, int l, int r) {
      if(r - l + 1 < pattern.size()) { return 0; }
      pattern = "#" + pattern;
      startMask.set();
      for(int i = 1; i < pattern.size(); ++i) {
        startMask &= (mask[pattern[i] - 'a'] >> i);
      }
      return (startMask >> (l - 1)).count() - (startMask >> (r - pattern.size() + 2)).count(); // number of set bits from l to r (similar to computing prefix sums)
    }
    
    vector<int> rangePatternPositions(string pattern, int l, int r) {
      vector<int> positions(rangePatternMatchCount(pattern, l, r));
      for(int i = l - 1, idx = 0; i < r - pattern.size() + 2 && idx < positions.size(); ++i) {
        if(startMask[i]) {
          positions[idx] = i + 1;
          ++idx;
        }
      }
      return positions;
    }

• An update in the text string can be reflected in the mask in constant time.

    void setBitForChar(int bit, char c) { mask[c - 'a'][bit] = 1; }
    void unsetBitForChar(int bit, char c) { mask[c - 'a'][bit] = 0; }
    
    void update(int idx, char ch) {
      unsetBitForChar(idx, text[idx]); // reseting previous character
      text[idx] = ch;
      setBitForChar(idx, text[idx]); // setting new character
    }

• Easy to implement and therefore, can be a replacement for many other string structures which are generally hard to implement. Example: Multi-pattern matching like Aho-Corasick can be performed using this algorithm by just iterating through all the patterns and calling optimizedStringMatching (computeMask should be called once before processing any pattern), if the sum of length of all strings is atmost |P|, then the complexity will be O(|T| + |P| * (|T| / K)).

Example

Note: bitset is visualised in reverse order of array for better understanding of bitwise operations

The string as an array and the mask values for character 'a' and 'b' (other characters are ignored because the entire text is made of only a's and b's):

mask[0] has 1's in the positions in which the text has 'a' and similarly mask[1] has 1's in the positions where the text has 'b'. Initially, all the positions in the startMask are set to 1 (assuming every position is a potential starting position for the pattern).

Iterating through the pattern from position 1, the first character in pattern is 'a', whose corresponding position in the mask array is 0. So, mask[0] is shifted left once ('a' should be the first character in the substring) and bitwise and (&) is performed with the startMask. This eliminates positions 1, 3, 5, 7 and 9 because the substrings (of length 1) formed from those starting positions are not 'a' in the original text (without the '#'):

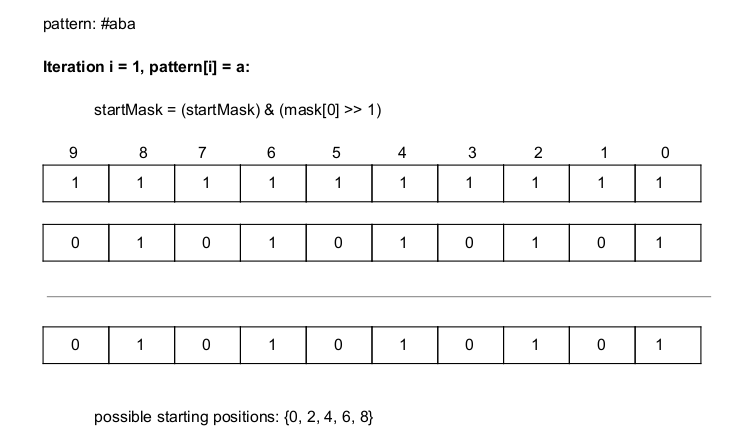
The second character in pattern is 'b', whose corresponding position in the mask array is 1. So, mask[1] is shifted left twice ('b' should be the second character in the substring) and bitwise and (&) is performed with the startMask. This eliminates position 8 because the substring (of length 2) formed from 8 is not 'ab' in the original text (without the '#'):

The final character in pattern is 'a' again, so mask[0] is shifted left thrice ('a' should be the third character in the substring) this time and bitwise and (&) is performed with the startMask. This does not eliminate any existing starting position in startMask (positions 0, 2, 4, 6) because the substrings of length 3 formed in the original text at these positions is 'aba'.

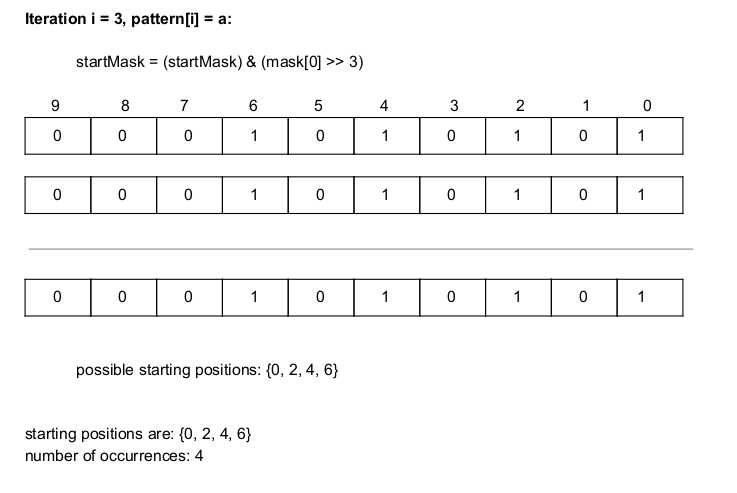
Therefore, the starting positions of aba in ababababa are 0, 2, 4 and 6.
The above example clarifies how the algorithm inductively finds the starting positions of a pattern by elimination.

Applications

Like any other string matching algorithm, this also has a wide range of applications:

Text find and replace

This algorithm is well suited for finding and replacing patterns, as updating a character can be done in constant time.

Finding all strings from a given dictionary in a text

Multi-pattern matching can be performed to find all the strings present in a dictionary, provided the sum of lengths of all the strings in the dictionary is not too large.

With this article at OpenGenus, you must have the complete idea of solving the string matching problem using bitset. Enjoy.