In this article, we have presented the Substitution method for finding the Time complexity of an algorithm in detail.

Table of Contents:

1. Introduction to Recurrence relations
2. Substitution Method
3. MCQs on Recurrence relations

Introduction to Recurrence relations

Recurrence relation is way of determining the running time of a recursive algorithm or program. It's a equation or a inequality that describes a functions in terms of its values and smaller inputs. Now before jumping on to various methods of solving recurrence relation, let's first take a look at the example of recurrence relation.
Let us consider T(n) to be the running time of a given problems on size n, the problem in our case will be finding the nth fibonacci number. Let F(n) denote the nth fibonacci number, therefore F(n) = F(n-1) + F(n-2) and T(0) = a , a is a constant.

The recurrence relation will be :
T(n) = c + T(n-1), where c is a constant

There are mainly four methods of solving recurrence relation:

1. Substitution method
2. Iteration method
3. Master method
4. Recursion tree method

Substitution method

In this article at OpenGenus, our primary focus is Solving recurrence relation via Substitution method, hence we will deep dive into the process through examples and explanations.

The whole working of the substitution method can be divided into two processes :

1. Take a guess at the solution
2. Find boundary conditions using the principles of mathematical induction and prove that the guess is correct

Note: Mathematical induction is a proof technique that is vastly used to prove formulas.

Now let us take an example:

Recurrence relation: T(1) = 1 and T(n) = 2T(n/2) + n for n > 1

Step 1: We guess that the solution is T(n) = O(n logn)

Step 2: Let's say c is a constant hence we need to prove that :
T(n) ≤ cn logn for all n ≥ 1

Step 3: Using the above statement we can assume that :
T(n) ≤ cn log(n/2) + n
T(n) = cn log(n) - cn log(2) + n
T(n) = cn log(n) - cn + n
T(n) = cn log(n) + n(1 - c)
hence T(n) ≤ cn log(n) for all c ≥ 1

Step 4: Now we need to put the values into the recurrence formula, T(2) = 2T(1) + 2 = 4 and T(3) = 2T(1) + 3 = 5, now our task to choose a c that perfectly fits our inequality obtained above in step 3, let say c = 2 :
4 ≤ 4log(2) and 5 ≤ 6log(3) perfectly satisfy the condition, hence we can conclude that T(n) ≤ 2n log n for all n ≥ 2, therefore T(n) = O(n log n)

MCQs on Recurrence relations

(i) Find the solution of given recurrence relation F(n) = 20F(n-1) - 25F(n-2), where F(0) = 4 and F(1) = 14

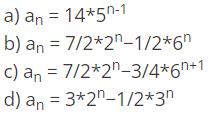
Ans : b

Explanation : First find the characteristic polynomial i.e. x^2-20x+36=0 in this case, having found the roots find the form of recurrence equation i.e. an=a(2^n)+b(18^n), find the value of a and b using equations F(0) = 4 and F(1) = 14 i.e. a=7/2 and b=-1/2, hence the answer is option b.

(ii) Determine the recurrence relation for the following series 1,7,31,127,499

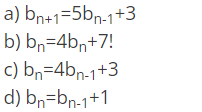
Ans : c

Explanation : On observing carefully, we see that the difference between the consecutive terms is a factor of 4, therefore 1.4=4,7.4=28,31.4=124 so on, ending term is 3 less than the next term therefore the answer will be option c.

(iii) Find the solution of given recurrence relation F(n) = 6T(n-1) - 8T(n-2), given that T(0) = 3 and T(1) = 5

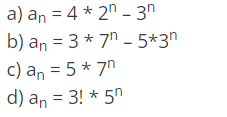
Ans : b

Explanation : Follow similar steps as mentioned in the first problem.

(iv) Find the solution of the recurrence relation T(n) = 5T(n-1) + 6T(n-2)

Ans : b

Explanation : Just check on the left side of the given equation for all the options individually, we find that 6n satisfies the equation hence answer is option b.

(v) Find the value of T(2) for the recurrence relation T(n) = 17T(n-1) + 30n, given that T(0) = 3

Ans : d

Explanation : First calculate the value for T(1) i.e. T(1) = 17T(0) + 30 = 81, now calculate value of T(2) by putting the value of T(1) in it i.e. T(2) = 17T(1) + 60 = 1437, that is our required answer.

Thank You!