Super Pow Problem [LeetCode: 372]

Problem Statement:

Your task is to calculate a^b mod 1337 where a is a positive integer and b is an extremely large positive integer given in the form of an array.

Example:

a = 9 & b = [6,7,3,4]
9^6734 -> The result will be too large.
we are asked to give the result as (9^6734)%1337 which is equal to 1075.

Table of Contents

• Problem Explanation
• Modulo Operator
• BruteForce Approach / Code / Time & Space Complexity
• Optimise Approach / Code / Time & Space Complexity

Problem Explanation:

In this problem we are required to find the value of a raise to power b where a is the base and b is its power. b is given in vector i.e all its digit is stored in vector.
Since the value will be to large so we are asked to give the result by doing the result modulo by 1337.

Modulo Operation in Multiplication:

(a*b) % mod = (a % mod * b % mod) % mod

This result is true. And we are gonna use this while solving the problem.
E.g :

    (10*6)%7 == 4
         or
     ((10%7) * (6%7))%7 = (3 * 6)%7 = 18%7 = 4

Bruteforce Approach:

Let us understand the approach with an example.
Let a = 9 & b = [9,5,3,4]
In this approach we will calculate the power of a raise to power b[i] and save it to b[i]. After that we calculate b[i] raise to power 10, (length of b - 1 - i) times. You can understand that from the picture guiven below :

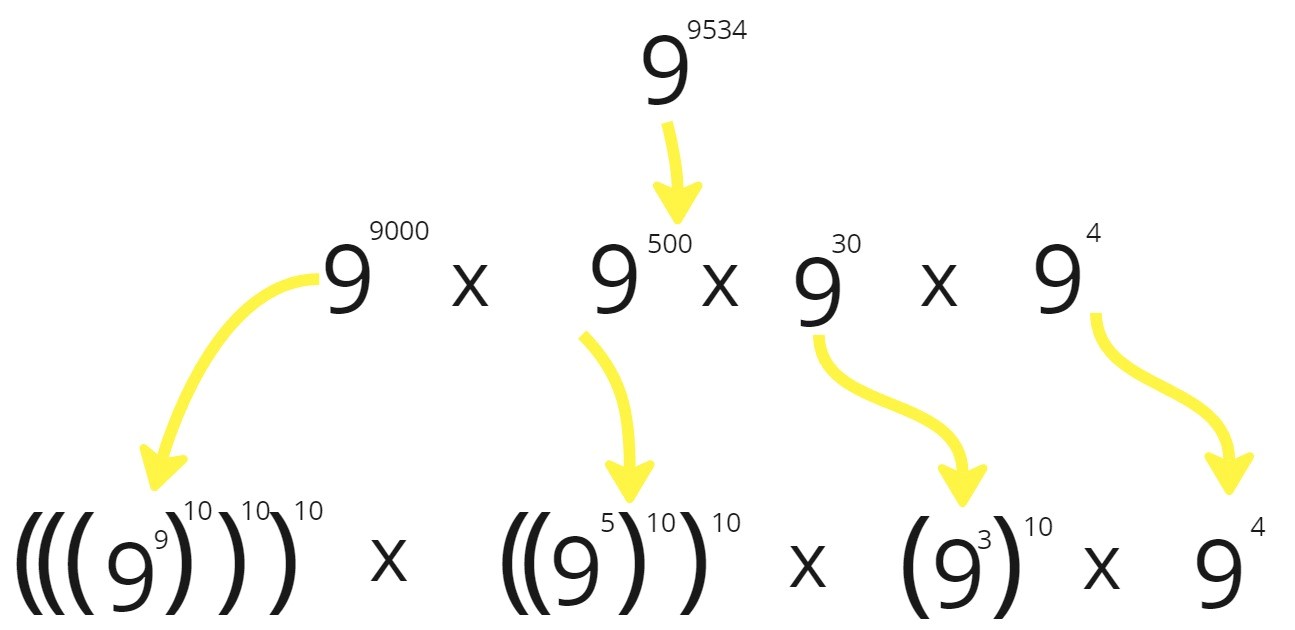
Points:

• Calculate a raise to power b[i] and save it to b[i].
• Calculate b[i] raise to power 10, j times where j is digit place of b[i].
• After all, Multiply all the elements of b[i].

Code:

class Solution {
public:
    int superPow(int a, vector<int>& b) {
       
        a = a%1337;

        for(int i=0;i<b.size();i++) {
            b[i] = calculate(a, b[i]);
        }

        for(int i=0;i<b.size();i++) {
            for(int j=b.size()-1-i;j>0;j--) {
                b[i] = calculate(b[i],10);
            }
        }

        int ans = 1;
        for(int i=0;i<b.size();i++) {
            ans = ans * b[i];
            ans = ans % 1337;
        }

        return ans;

    }

    int calculate(int base, int power) {
        int ans = 1;
        for(int i=0;i<power;i++) {
            ans = (ans * base)%1337;
        }
        return ans;
    }
};

Time & Space Complexity:

Time Complexity : O(n^2) where n is the length of vector b.
Space Complexity : O(1)

Optimise Approach:

Let us understand the approach with an example.
Let a = 9 & b = [9,5,3,4]
We can break the number in following manner.

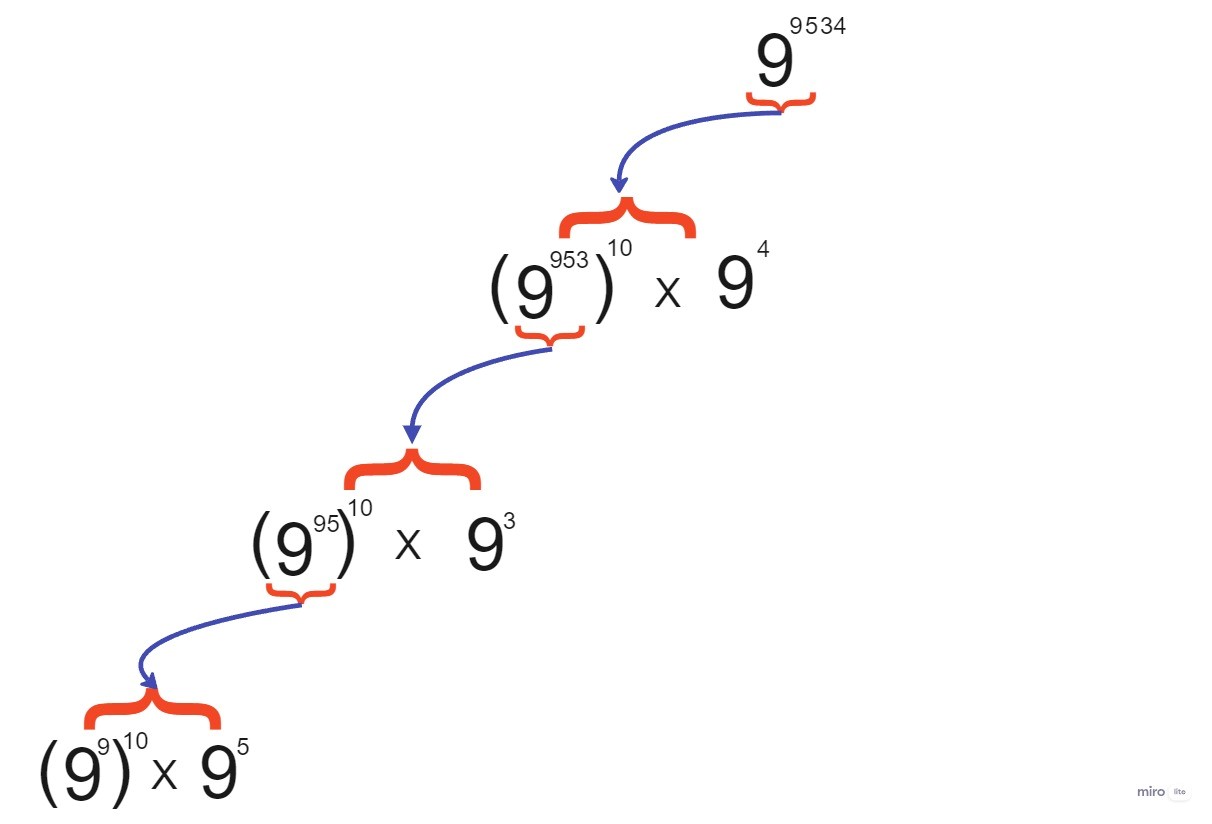
which can be written as :

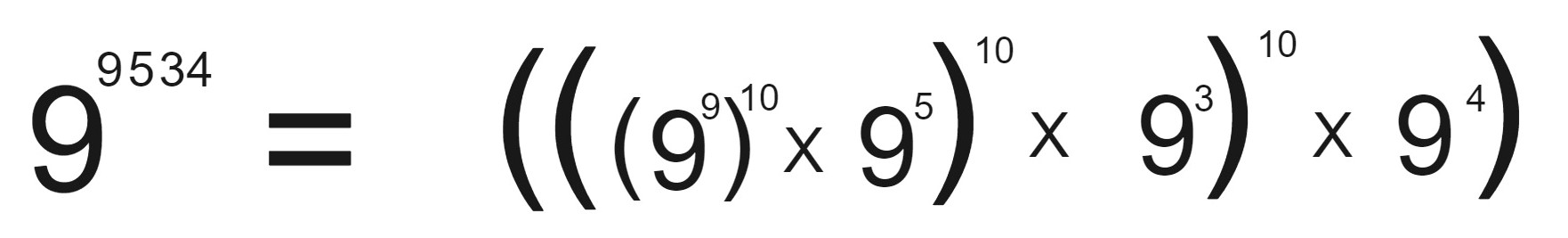
We can write the number in multiplication form so that we can apply the Modulo Operation in each multiplication so that the number doesn't go out of range.

Points:

• Calculate a raise to power b[i].
• Calculate the above value by raising it to power 10.
• Repeat the above to steps, till i is less than length of b.

Code:

class Solution {
public:
    int superPow(int a, vector<int>& b) {
        
        int temp = 1, ans;
        a = a%1337;
        for(int i=0;i<b.size();i++) {
            temp = (temp*calculate(a,b[i]))%1337;
            ans = temp;
            temp = calculate(temp,10);
        }
        return ans;
    }
    
    //Calculate the power
    
    /*Here we will calculate the result "base" raised to power "power" by multiplying base
    power times using a for loop and also taking modulo on every multiplication so that 
    the result doesn't go out of range. */
    
    int calculate(int base, int power) {
        int ans = 1;
        for(int i=0;i<power;i++) {
            ans = (ans * base)%1337;
        }
        return ans;
    }
};

Time & Space Complexity:

Time Complexity : O(n) where n is the length of vector b.
Space Complexity : O(1)