Terms used in Neural Networks

The common terms used in Neural Networks are:

• Convolution
• Max Pooling
• Fully Connected Layer
• Softmax Activation Function
• Rectified Linear Units

Convolution

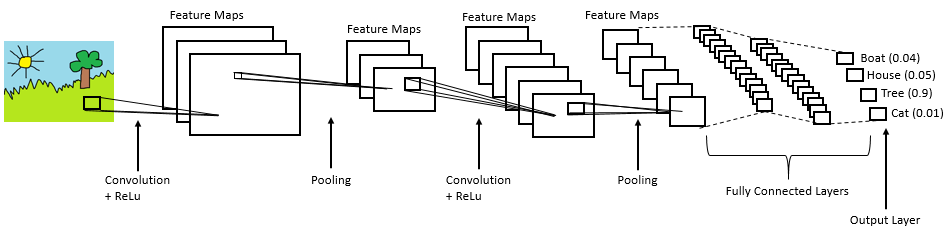
Convolution is one of the main building blocks of a CNN. The term convolution refers to the mathematical combination of two functions to produce a third function.the convolution is applied on the input data using a convolution filter to produce a feature map.It merges two sets of information.In the case of a CNN, the convolution is performed on the input data with the use of a filter or kernel (these terms are used interchangeably) to then produce a feature map.We execute a convolution by sliding the filter over the input. At every location, a matrix multiplication is performed and sums the result onto the feature map.We execute a convolution by sliding the filter over the input. At every location, a matrix multiplication is performed and sums the result onto the feature map.

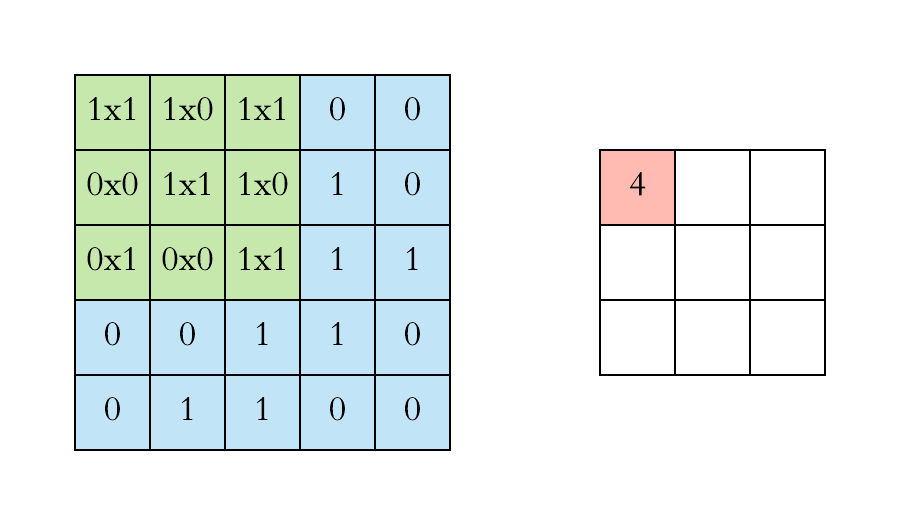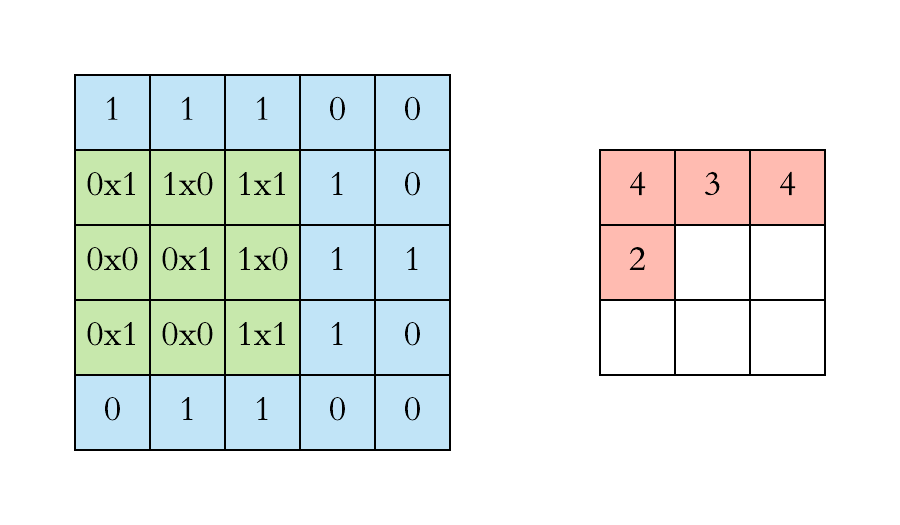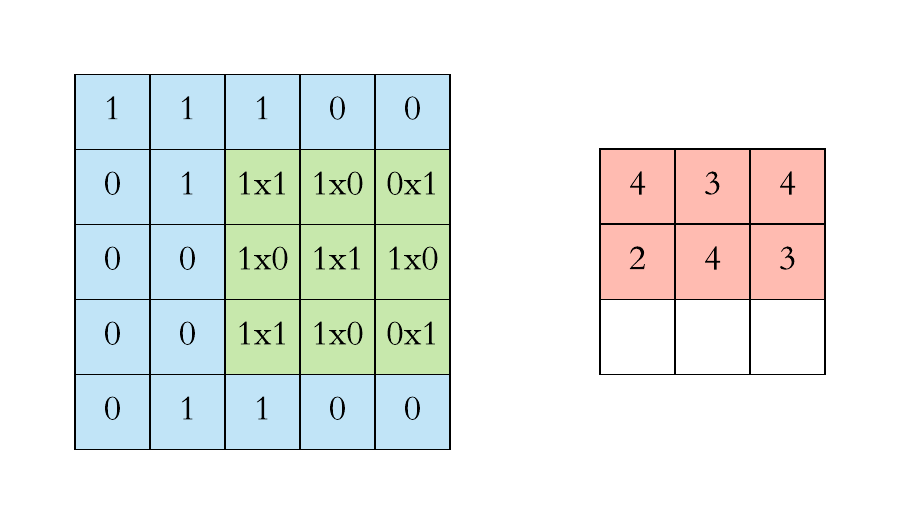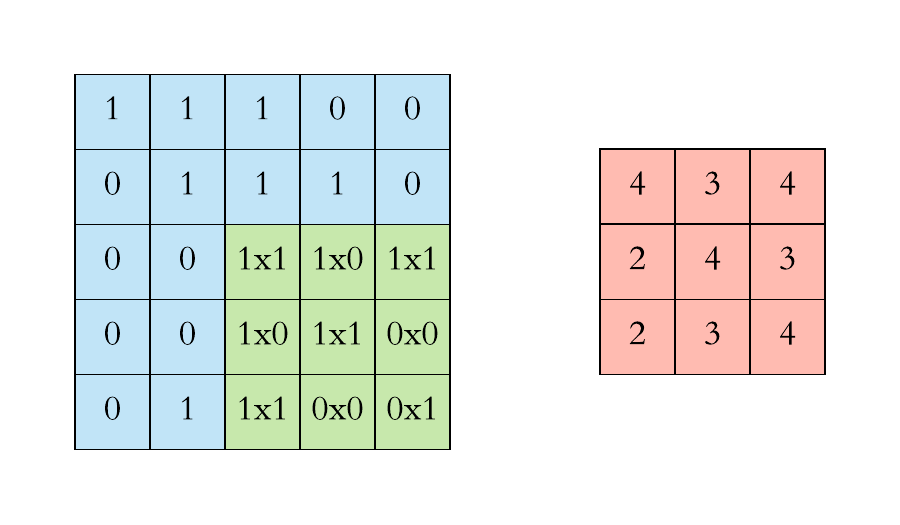
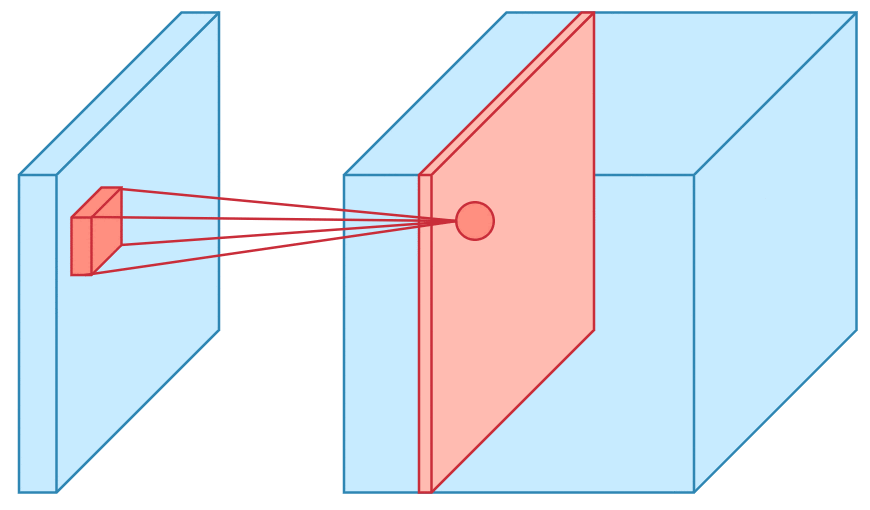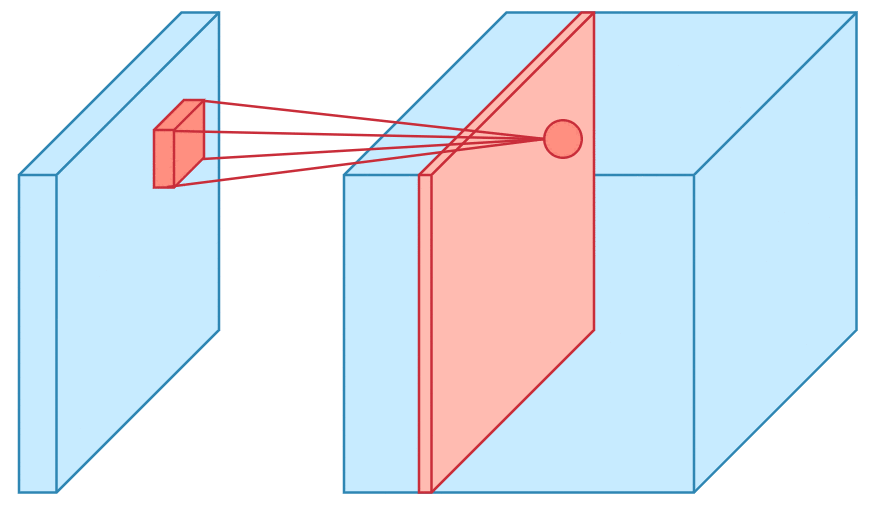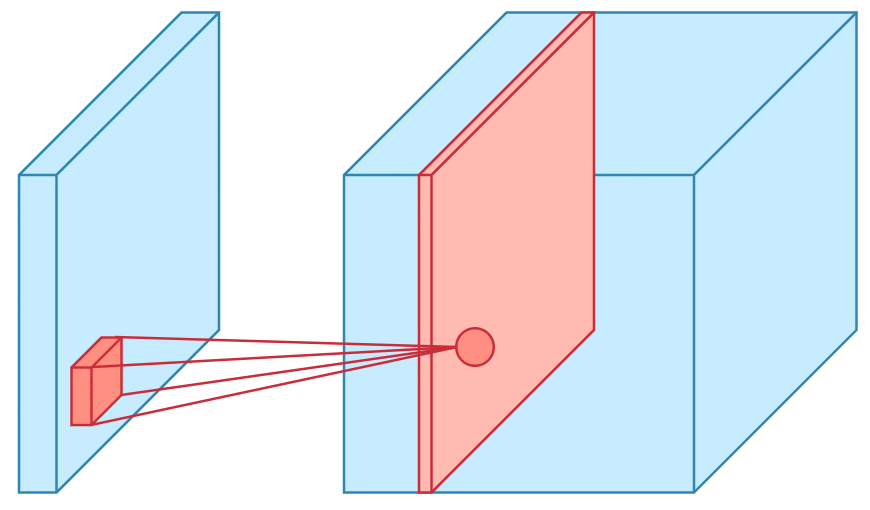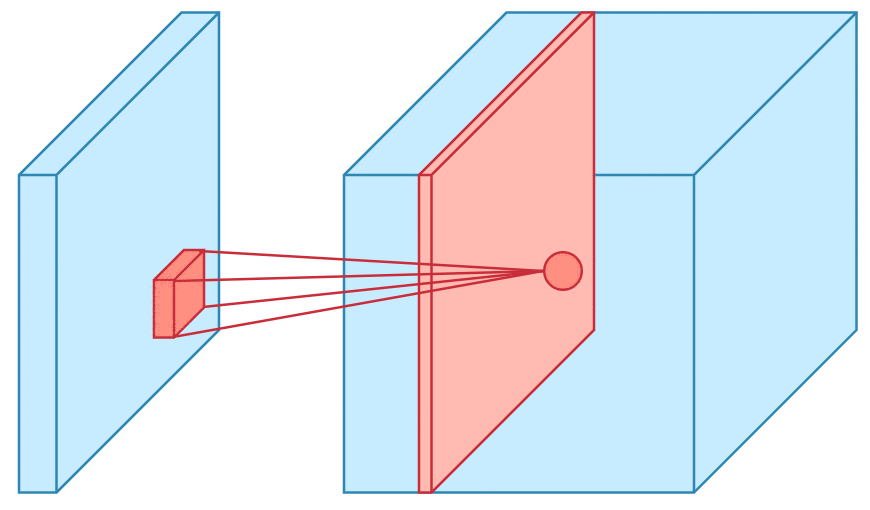
Max Pooling

Pooling layers section would reduce the number of parameters when the images are too large. Spatial pooling also called subsampling or downsampling which reduces the dimensionality of each map but retains the important information.This shortens the training time and controls overfitting.One Term used in Max Pooling is Stride.Stride is the number of pixels shifts over the input matrix. When the stride is 1 then we move the filters to 1 pixel at a time. When the stride is 2 then we move the filters to 2 pixels at a time and so on. The below figure shows convolution would work with a stride of 2. Spatial pooling can be of different types:

1.Max Pooling
2.Average Pooling
3.Sum Pooling
Max pooling take the largest element from the rectified feature map. Taking the largest element could also take the average pooling.Sum of all elements in the feature map call as sum pooling.

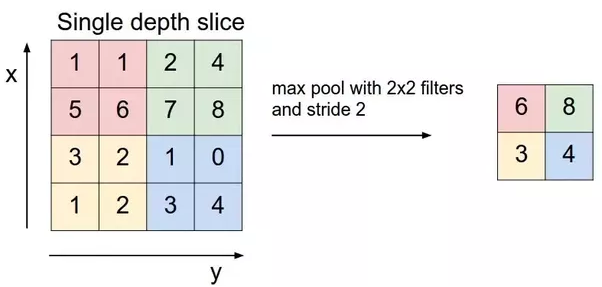
Fully Connected Layer

The layer we call as FC layer, we flattened our matrix into vector and feed it into a fully connected layer like neural network.feature map matrix will be converted as vector (x1, x2, x3, …). With the fully connected layers, we combined these features together to create a model. Finally, we have an activation function such as softmax or sigmoid to classify the outputs as cat, dog, car, truck etc.

Softmax Activation Function

The sigmoid function can be applied easily, the ReLUs will not vanish the effect during your training process. However, when you want to deal with classification problems, they cannot help much. Simply speaking, the sigmoid function can only handle two classes, which is not what we expect.

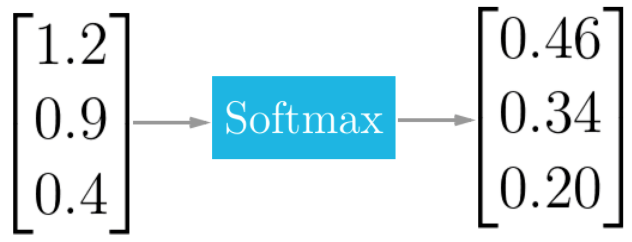
The softmax function squashes the outputs of each unit to be between 0 and 1, just like a sigmoid function. But it also divides each output such that the total sum of the outputs is equal to 1 (check it on the figure above).

The output of the softmax function is equivalent to a categorical probability distribution, it tells you the probability that any of the classes are true.

Mathematically the softmax function is shown below, where z is a vector of the inputs to the output layer (if you have 10 output units, then there are 10 elements in z). And again, j indexes the output units, so j = 1, 2, ..., K.

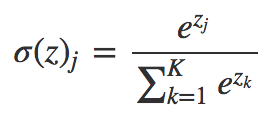
Rectified Linear Units

Deep learning networks use rectified linear units (ReLUs) for the hidden layers. A rectified linear unit has output 0 if the input is less than 0, and raw output otherwise. That is, if the input is greater than 0, the output is equal to the input. ReLUs' machinery is more like a real neuron in your body.

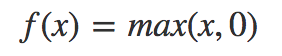
ReLU activations are the simplest non-linear activation function you can use, obviously. When you get the input is positive, the derivative is just 1, so there isn't the squeezing effect you meet on backpropagated errors from the sigmoid function. Research has shown that ReLUs result in much faster training for large networks. Most frameworks like TensorFlow and TFLearn make it simple to use ReLUs on the the hidden layers, so you won't need to implement them yourself.