Internet provides access to plethora of information today. Whatever we need is just a Google (search) away. However, when we have so much of information, the challenge is to segregate between relevant and irrelevant information.
When our brain is fed with a lot of information simultaneously, it tries hard to understand and classify the information between useful and not-so-useful information. We need a similar mechanism to classify incoming information as useful or less-useful in case of Neural Networks.
Well, activation functions help the network to find the difference between these two cases. They help the network use the useful information and suppress the irrelevant data points.

what is activation function:

Activation functions are an extremely important feature of the artificial neural networks. They basically decide whether a neuron should be activated or not. Whether the information that the neuron is receiving is relevant for the given information or should it be ignored.
The activation function is the non linear transformation that we do over the input signal. This transformed output is then sen to the next layer of neurons as input.

Types of activation function:

1. Identity
2. Binary Step
3. Sigmoid
4. Tanh
5. ReLU
6. Leaky ReLU
7. Softmax

Linear function:

If we don't apply a activation function then the output signal would be simple linear function.
A linear function is easy to solve but they are limited in their complexity and have less power t learn complex functional mappings from data.
Also without activation function our neural networks would not be able to learn and other kinds of data such as images, videos, audio, speech etc.

Identity function

An identity function, also called an identity relation or identity map or identity transformation, is a function that always returns the same value that was used as its argument.
Itis defined as -
f(x) = x

As it always returns same value, so it gives same output always. It is not used.

Binary Step Function

The first thing that comes to our mind when we have an activation function would be a threshold based classifier i.e. whether or not the neuron should be activated. If the value Y is above a given threshold value then activate the neuron else leave it deactivated.
It is defined as –
f(x) = 1, x>=0
f(x) = 0, x<0

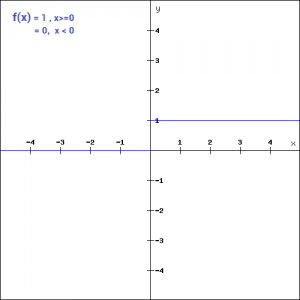
The binary function is extremely simple. It can be used while creating a binary classifier. When we simply need to say yes or no for a single class, step function would be the best choice, as it would either activate the neuron or leave it to zero.

Sigmoid function

Sigmoid is a widely used activation function. It is of the form-

f(x)=1/(1+e^-x)
Let’s plot this function and take a look of it.

This is a smooth function and is continuously differentiable. The biggest advantage that it has over step and linear function is that it is non-linear. This is an incredibly cool feature of the sigmoid function. This essentially means that when I have multiple neurons having sigmoid function as their activation function – the output is non linear as well. The function ranges from 0-1 having an S shape.

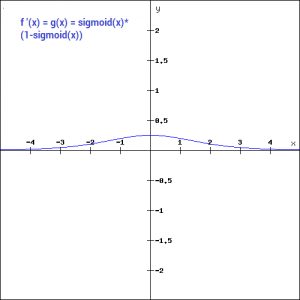
Let’s take a look at the gradient of the sigmoid function as well.

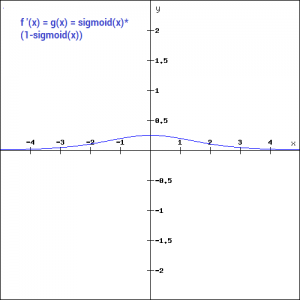
The gradient is very high between the values of -3 and 3 but gets much flatter in other regions. How is this of any use?
This means that in this range small changes in x would also bring about large changes in the value of Y. So the function essentially tries to push the Y values towards the extremes. This is a very desirable quality when we’re trying to classify the values to a particular class.

Sigmoids are widely used even today but we still have a problems that we need to address. As we saw previously – the function is pretty flat beyond the +3 and -3 region. This means that once the function falls in that region the gradients become very small. This means that the gradient is approaching to zero and the network is not really learning.
Another problem that the sigmoid function suffers is that the values only range from 0 to 1. This meas that the sigmoid function is not symmetric around the origin and the values received are all positive. So not all times would we desire the values going to the next neuron to be all of the same sign. This can be addressed by scaling the sigmoid function. That’s exactly what happens in the tanh function. let’s read on.

Tanh function

The tanh function is very similar to the sigmoid function. It is actually just a scaled version of the sigmoid function.
tanh(x)=2sigmoid(2x)-1

It can be directly written as –
tanh(x)=2/(1+e^(-2x)) -1

Tanh works similar to the sigmoid function but is symmetric over the origin. it ranges from -1 to 1.

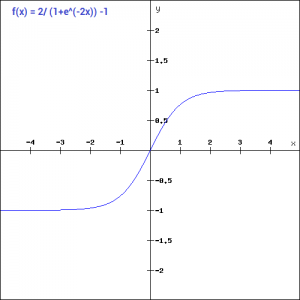
It basically solves our problem of the values all being of the same sign. All other properties are the same as that of the sigmoid function. It is continuous and differentiable at all points. The function as you can see is non linear so we can easily backpropagate the errors.

Let’s have a look at the gradient of the tan h function.

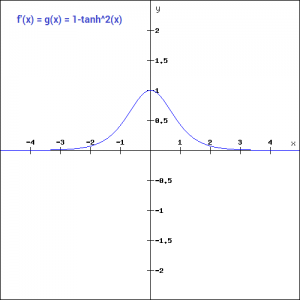
The gradient of the tanh function is steeper as compared to the sigmoid function. Our choice of using sigmoid or tanh would basically depend on the requirement of gradient in the problem statement. But similar to the sigmoid function we still have the vanishing gradient problem. The graph of the tanh function is flat and the gradients are very low.

ReLU function

The ReLU function is the Rectified linear unit. It is the most widely used activation function. It is defined as-
f(x)=max(0,x)

It can be graphically represented as-

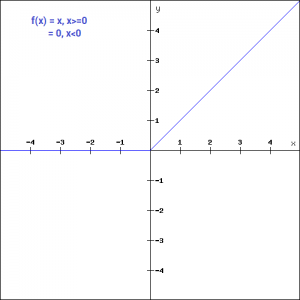
ReLU is the most widely used activation function while designing networks today. First things first, the ReLU function is non linear, which means we can easily backpropagate the errors and have multiple layers of neurons being activated by the ReLU function.

**The main advantage of using the ReLU function over other activation functions is that it does not activate all the neurons at the same time.

What does this mean ? If you look at the ReLU function if the input is negative it will convert it to zero and the neuron does not get activated. This means that at a time only a few neurons are activated making the network sparse making it efficient and easy for computation.

Let’s look at the gradient of the ReLU function.

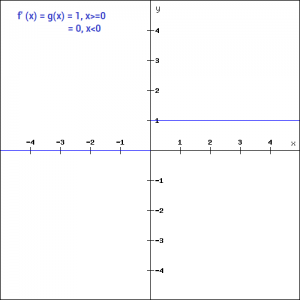
But ReLU also falls a prey to the gradients moving towards zero. If you look at the negative side of the graph, the gradient is zero, which means for activations in that region, the gradient is zero and the weights are not updated during back propagation. This can create dead neurons which never get activated. When we have a problem, we can always engineer a solution.

Leaky ReLU function

Leaky ReLU function is nothing but an improved version of the ReLU function. As we saw that for the ReLU function, the gradient is 0 for x<0, which made the neurons die for activations in that region. Leaky ReLU is defined to address this problem. Instead of defining the Relu function as 0 for x less than 0, we define it as a small linear component of x. It can be defined as-
f(x)= ax, x<0
f(x)= x, x>=0

What we have done here is that we have simply replaced the horizontal line with a non-zero, non-horizontal line. Here a is a small value like 0.01 or so. It can be represented on the graph as-

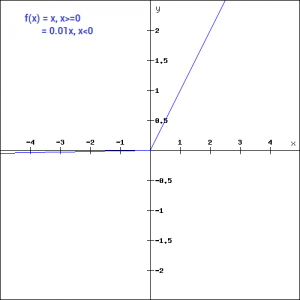
The main advantage of replacing the horizontal line is to remove the zero gradient. So in this case the gradient of the left side of the graph is non zero and so we would no longer encounter dead neurons in that region. The gradient of the graph would look like –

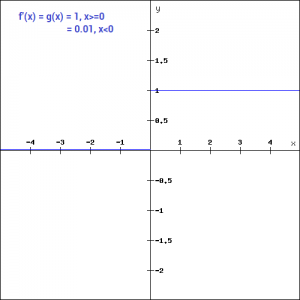
Similar to the Leaky ReLU function, we also have the Parameterised ReLU function. It is defined similar to the Leaky ReLU as –
f(x)= ax, x<0
f(x)= x, x>=0

However, in case of a parameterised ReLU function, ‘a‘ is also a trainable parameter. The network also learns the value of ‘a‘ for faster and more optimum convergence. The parametrised ReLU function is used when the leaky ReLU function still fails to solve the problem of dead neurons and the relevant information is not successfully passed to the next layer.

Softmax function

The softmax function is also a type of sigmoid function but is handy when we are trying to handle classification problems. The sigmoid function as we saw earlier was able to handle just two classes. What shall we do when we are trying to handle multiple classes. Just classifying yes or no for a single class would not help then. The softmax function would squeeze the outputs for each class between 0 and 1 and would also divide by the sum of the outputs. This essentially gives the probability of the input being in a particular class. It can be defined as –

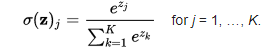
Let’s say for example we have the outputs as-

[1.2 , 0.9 , 0.75], When we apply the softmax function we would get [0.42 , 0.31, 0.27]. So now we can use these as probabilities for the value to be in each class.
The softmax function is ideally used in the output layer of the classifier where we are actually trying to attain the probabilities to define the class of each input.