
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 35 minutes | Coding time: 12 minutes
X-fast trie is a data structure used to store integers from a bounded domain. It is a bitwise trie, i.e. a binary tree where each subtree stores values having binary representations with common prefix. X-fast trie provides access to a sorted tree that treats integers as if they were words of w bits, which allows storing integers as a trie of words. Its advantage is that operations can be performed in constant time depending on the size of the universe, not the number of items in trie.
It is expected to perform five operations:
- find(x): Find x in the given trie.
- predecessor(x): Return the largest element in domain less than or equal to x.
- successor(x): Return the smallest element in domain less greater or equal to x.
- insert(x, v): Insert an element x into trie pointing to value v.
- delete(x): Delete an element x from trie.
X-fast trie is used to perform extremely fast operations in a bounded universe, and is a space efficient alternative to van Emde Boas trees.
Height of the structure is log2U where U is the size of the universe/ dataset.
Hash tables do not perform well for predecessor or successor queries, and so X-fast tries can be used in those cases which gives time complexity of log2U.
The structure of X-fast trie is similar to a binary tree.
Every internal node represents some prefix while leaf nodes represents the values form 0 to U - 1. The root represents an empty prefix.
At any node, moving to left child appends 0 to the prefix and moving to right child appends 1 to the prefix. Thus the left child of 101... will represent 1010.. while right child will represent 1011...
Every level of trie is implemented as a hash table, thus there are log2U hash tables. Internal nodes are stored only if their subtree contains one or more leaves. The leaf nodes stores pointers to their predecessor and successors, thus giving a doubly linked list at the leaves level. All these nodes are stored in the respective hash tables. If an internal node does not have a right child, the right pointer will point to smallest leaf in left subtree. Similarly, if there is no left child, left child pointer will point to largest node in right subtree. These pointers are called descendant pointers.
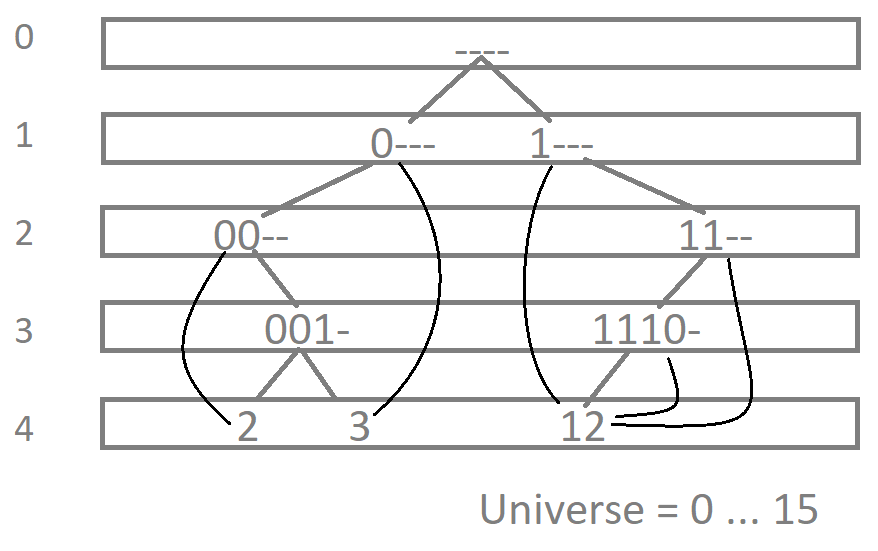
The tree above represents a trie with universe size U = 16. The nodes stored are 2, 3 and 12. Dark lines represent descendant pointers. Only nodes required by leaf nodes are stored in respective hash tables. Root, i.e. only node at level 0 is empty prefix.
Algorithm
X-Fast trie will support the following operations:
- find
- successor and predecessor
- insert
- delete
Find operation
- find(k): Find the element k in trie.
Since the leaf nodes are saved as a hash table, this can be done
directly in O(1) time.successor and predecessor operation
- successor(k) and predecessor(k): Successor is the node with smallest element greater than or equal to k, while predecessor is largest element smaller than or equal to k in trie. This node will have longest common prefix with k.
1. Binary search the levels, each of which is a hash table.
2. Set low = 0 and high = h, where h = height of the tree.
3. Repeatedly set mid = (low + high) / 2, and check if hash table has contains
the prefix of k. If it does, that means target node is between levels mid
and high(inclusive). So set low = mid.
Otherwise, target node is between low and mid, so set high = mid.
4. The node reached will have longest common prefix with k. Since k is not in trie,
either left or right child pointer is empty. So descendant pointer is used to
directly reach the leaf node.
5. After reaching leaf node, double linked list needs to be traversed forward or
backward just once to get wanted node, or to determine that no such element
exists.Insert operation
- insert(k, v): To insert the key value pair (k, v)
1. Find the predecessor and successor of k.
2. Create a new node representing k. Have the node store value v.
3. Add the node between predecessor and successor in doubly linked list.
4. Start and root and traverse down to the leaf while creating missing
internal nodes.Delete operation
- delete(k):
1. Find the leaf node with key k using hash table.
2. Delete the node and connect its successor and predecessor in doubly-linked
lists.
3. Traverse upwards till root and delete all internal nodes that had only k
inside its subtrees. Update descendant pointers to point to either its
successor or predecessor appropriately.Complexity
- Time complexity:
- Find: O(1)
- Successor, Predecessor: O(log2log2U)
- Insert: O(log2U)
- Delete: O(log2U)
- Space complexity: O(N log2U)
Where N is count of values stored and U is universe size.
Implementations
C++ 11
/*
/*
* c++ 11 code to construct an Xfast trie. Complete the destructor
* as an exercise to perform delete on all Node objects
*/
#include <iostream>
#include <unordered_map>
#include <vector>
struct Node{
int level;
int key;
// also used by leaf nodes to simulate linked list
Node *left, *right;
Node(){
level = -1;
left = nullptr;
right = nullptr;
}
};
class XfastTrie{
int w;
std::vector<std::unordered_map> hash_table;
int getDigitCount(int x){
int count = 0;
for(; x > 0; x >>= 1, ++count);
return count;
}
int leftChild(int x){
return (x << 1);
}
int rightChild(int x){
return ((x << 1) | 1);
}
Node *getLeftmostLeaf(Node *parent){
while(parent->level != w){
if(parent->left != nullptr)
parent = parent->left;
else
parent = parent->right;
}
return parent;
}
Node * getRightmostLeaf(Node *parent){
while(parent->level != w){
if(parent->right != nullptr)
parent = parent->right;
else
parent = parent->left;
}
return parent;
}
public:
XfastTrie(int U){
w = getDigitCount(U);
hash_table.assign(w + 1, std::unordered_map<int, Node *>());
Node *root = new Node();
root->level = 0;
hash_table[0][0] = root;
}
Node* find(int k){
if(hash_table[w].find(k) == hash_table[w].end())
return nullptr;
return hash_table[w][k];
}
Node* successor(int k){
int low = 0,
high = w + 1,
mid, prefix;
Node *tmp = nullptr;
while(high - low > 1){
mid = (low + high) >> 1;
prefix = k >> (w - mid);
if(hash_table[mid].find(prefix) == hash_table[mid].end())
high = mid;
else{
low = mid;
tmp = hash_table[mid][prefix];
}
}
if(tmp == nullptr || tmp->level == 0)
// occours on first insertion
return nullptr;
if(tmp->level == w)
return tmp;
// use descendant node
if((k >> (w - tmp->level - 1)) & 1)
tmp = tmp->right;
else
tmp = tmp->left;
if(tmp->key < k){
return tmp->right;
}
return tmp;
}
Node* predecessor(int k){
// completely same as successor except lst section
int low = 0,
high = w + 1,
mid, prefix;
Node *tmp = nullptr;
while(high - low > 1){
mid = (low + high) >> 1;
prefix = k >> (w - mid);
if(hash_table[mid].find(prefix) == hash_table[mid].end())
high = mid;
else{
low = mid;
tmp = hash_table[mid][prefix];
}
}
if(tmp == nullptr || tmp->level == 0)
// occours on first insertion
return nullptr;
if(tmp->level == w)
return tmp;
// use descendant node
if((k >> (w - tmp->level - 1)) & 1)
tmp = tmp->right;
else
tmp = tmp->left;
if(tmp->key > k){
return tmp->left;
}
return tmp;
}
void insert(int k){
Node *node = new Node();
node->key = k;
node->level = w;
// update linked list
Node *pre = predecessor(k);
Node *suc = successor(k);
if(pre != nullptr){
if(pre->level != w){
std::cout << "Wierd level " << pre->level << '\n';
}
node->right = pre->right;
pre->right = node;
node->left = pre;
}
if(suc != nullptr){
if(suc->level != w){
std::cout << "Wierd level " << suc->level << '\n';
}
node->left = suc->left;
suc->left = node;
node->right = suc;
}
int lvl = 1, prefix;
while(lvl != w){
prefix = k >> (w - lvl);
if(hash_table[lvl].find(prefix) == hash_table[lvl].end()){
Node *inter = new Node();
inter->level = lvl;
hash_table[lvl][prefix] = inter;
if(prefix & 1)
hash_table[lvl - 1][prefix >> 1]->right = inter;
else
hash_table[lvl - 1][prefix >> 1]->left = inter;
}
++lvl;
}
hash_table[w][k] = node;
if(k & 1)
hash_table[w - 1][k >> 1]->right = node;
else
hash_table[w - 1][k >> 1]->left = node;
// update descendant pointers
prefix = k;
lvl = w - 1;
while(lvl != 0){
prefix = prefix >> 1;
if(hash_table[lvl][prefix]->left == nullptr)
hash_table[lvl][prefix]->left = getLeftmostLeaf(hash_table[lvl][prefix]->right);
else if(hash_table[lvl][prefix]->right == nullptr)
hash_table[lvl][prefix]->right = getRightmostLeaf(hash_table[lvl][prefix]->left);
--lvl;
}
if(hash_table[0][0]->left == nullptr){
hash_table[0][0]->left = getLeftmostLeaf(hash_table[0][0]->right);
}
if(hash_table[0][0]->right == nullptr){
hash_table[0][0]->right = getRightmostLeaf(hash_table[0][0]->left);
}
}
~XfastTrie(){
//
}
};
int main(){
XfastTrie trie(1 << 5);
std:: cout << "insert 1, 5, 11, 12\n";
trie.insert(5);
trie.insert(11);
trie.insert(12);
trie.insert(1);
std::cout << "Successor of key 2:\n";
Node *tmp = trie.successor(2);
if(tmp != nullptr){
std::cout << tmp->key << '\n';
}
std::cout << "Predecessor of key 13:\n";
tmp = trie.predecessor(13);
if(tmp != nullptr){
std::cout << tmp->key << '\n';
}
}
Applications
- X-fast tries are used in database systems.
- X-fast tries are mostly used when successor/predecessor queries are often done upon the data.
