Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 25 minutes
Logistic Regression is one of the supervised Machine Learning algorithms used for classification i.e. to predict discrete valued outcome. It is a statistical approach that is used to predict the outcome of a dependent variable based on observations given in the training set.
Advantages
-
Logistic Regression is one of the simplest machine learning algorithms and is easy to implement yet provides great training efficiency in some cases. Also due to these reasons, training a model with this algorithm doesn't require high computation power.
-
The predicted parameters (trained weights) give inference about the importance of each feature. The direction of association i.e. positive or negative is also given. So we can use logistic regression to find out the relationship between the features.
-
This algorithm allows models to be updated easily to reflect new data, unlike decision trees or support vector machines. The update can be done using stochastic gradient descent.
-
Logistic Regression outputs well-calibrated probabilities along with classification results. This is an advantage over models that only give the final classification as results. If a training example has a 95% probability for a class, and another has a 55% probability for the same class, we get an inference about which training examples are more accurate for the formulated problem.
-
In a low dimensional dataset having a sufficient number of training examples, logistic regression is less prone to over-fitting.
-
Rather than straight away starting with a complex model, logistic regression is sometimes used as a benchmark model to measure performance, as it is relatively quick and easy to implement.
-
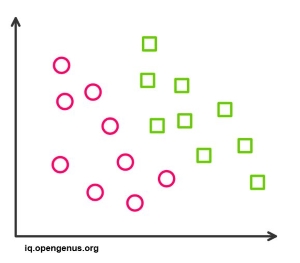
Logistic Regression proves to be very efficient when the dataset has features that are linearly separable.
-
It has a very close relationship with neural networks. A neural network representation can be perceived as stacking together a lot of little logistic regression classifiers.
-
Due to its simple probabilistic interpretation, the training time of logistic regression algorithm comes out to be far less than most complex algorithms, such as an Artificial Neural Network.
-
This algorithm can easily be extended to multi-class classification using a softmax classifier, this is known as Multinomial Logistic Regression.
-
Resultant weights found after training of the logistic regression model, are found to be highly interpretable. The weight w_i can be interpreted as the amount log odds will increase, if x_i increases by 1 and all other x's remain constant. i here refers to any training example from i = 0 to n .
Disadvantages
-
Logistic Regression is a statistical analysis model that attempts to predict precise probabilistic outcomes based on independent features. On high dimensional datasets, this may lead to the model being over-fit on the training set, which means overstating the accuracy of predictions on the training set and thus the model may not be able to predict accurate results on the test set. This usually happens in the case when the model is trained on little training data with lots of features. So on high dimensional datasets, Regularization techniques should be considered to avoid over-fitting (but this makes the model complex). Very high regularization factors may even lead to the model being under-fit on the training data.
-
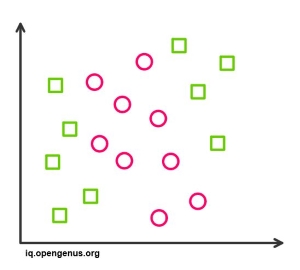
Non linear problems can't be solved with logistic regression since it has a linear decision surface. Linearly separable data is rarely found in real world scenarios. So the transformation of non linear features is required which can be done by increasing the number of features such that the data becomes linearly separable in higher dimensions.
-
It is difficult to capture complex relationships using logistic regression. More powerful and complex algorithms such as Neural Networks can easily outperform this algorithm.
-
The training features are known as independent variables. Logistic Regression requires moderate or no multicollinearity between independent variables. This means if two independent variables have a high correlation, only one of them should be used. Repetition of information could lead to wrong training of parameters (weights) during minimizing the cost function. Multicollinearity can be removed using dimensionality reduction techniques.
-
In Linear Regression independent and dependent variables should be related linearly. But Logistic Regression requires that independent variables are linearly related to the log odds (log(p/(1-p)).
-
Only important and relevant features should be used to build a model otherwise the probabilistic predictions made by the model may be incorrect and the model's predictive value may degrade.
-
The presence of data values that deviate from the expected range in the dataset may lead to incorrect results as this algorithm is sensitive to outliers.
-
Logistic Regression requires a large dataset and also sufficient training examples for all the categories it needs to identify.
-
It is required that each training example be independent of all the other examples in the dataset. If they are related in some way, then the model will try to give more importance to those specific training examples. So, the training data should not come from matched data or repeated measurements. For example, some scientific research techniques rely on multiple observations on the same individuals. This technique can't be used in such cases.
Applications
- Email : Spam / not Spam ?
- Online Credit Card Transactions : Fraudulent (Yes/No)
With this article at OpenGenus, you must have the complete idea of Advantages and Disadvantages of Logistic Regression. Enjoy.