
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Key Takeaways (Amdahl’s law)
- Amdahl's law was presented by a computer scientist named Gene Amdahl.
- It is used to calculate the theoretical speedup the system will gain when we use multiple processors.
- Serial programs are the programs which can't be run in parallel and must be executed sequentially.
- Parallel programs are the programs that can be executed parallely
- Speedup quantifies the performance improvement achieved by parallelizing a program.
- The Amdahl's law gives a formula for calculating `speedup`
Table of Content
- Introduction
1.1. Serial programs
1.2. Parallel programs
1.3. Speedup
1.4. Efficiency
1.5. Workload
1.6. Latency - Definition
- Derivition
- Examples
- Advatages
- Disadvatages
Introduction
Amdahl's law was presented by a computer scientist named Gene Amdahl at the American Federation of Information processing Societies (AFIPS) Spring Joint Computer conference in 1967, From there it got its name.
It is used to calculate the theoretical speedup the system will gain when we use multiple processors. For example if your manager asked you to that company requires to improve existing system then How many processors should be added, given that a program requires t units time for completing in single thread and p units time will always run in single thread. From this problem we can clearly see that no matter how many processors we introduce to the system it will will complete the task in minimum p units.
Serial Programs
Serial programs are the programs which can't be run in parallel and must be executed sequentially meaning one program will execute at a time and next program will execute only when the previous program in executed completely.
In the context of Amdahl's Law, these are the portions of the program that cannot benefit from multiple processors and create a bottleneck to overall performance.
Parallel Programs
Parallel programs are the programs that can be executed parallely meaning multiple programs can be executed at same time on different processors.
In context of Amdahl's law these are the programs that can be parallelized to improve the overall performance of the system.
Speedup
Speedup refers to the ratio of the time taken to execute a program on a single processor to the time taken on multiple processors.
speedup = $\frac{T_{1}}{T_{p}}$
In the context of Amdahl's Law, speedup quantifies the performance improvement achieved by parallelizing a program.
Efficiency
In context Amdahl's law, efficiency can be defined as how effectively multiple processors are utilized. It is calculated as the ratio of the speedup to the number of processors. Higher efficiency indicates better utilization of resources.
efficiency = $\frac{speedup}{n_{processors}}$
Workload
Workload refers to the amount of computational work that needs to be done by a program. In the context of Amdahl's Law, Workload is crucial for determining which parts of the program can be parallelized and which parts are sequential.
Latency
In the context of Amdahl's Law, latency refer to the time it takes to complete a specific task in both serial and parallel scenarios. Reducing latency is one of the goals of parallelization, as parallel processing can help in achieving tasks faster by dividing the workload among multiple processors.
Definition
Amdahl's law is a formula which gives the theoretical speedup in latency of the execution of a task at fixed workload that can be expected of a system whose resources are improved.
In simple words, The Amdahl's law gives a formula for calculating speedup, It tells that what is the maximum speedup a system can gain after adding multiple processors. The limit of speedup depends on the bottleneck caused due to the serial programs. After certain number of processors the system will not gain any speedup, The Amdahl's law is used to tell that limit.
speedup = $\frac{1}{(1 - P) + \frac{P}{N}}$
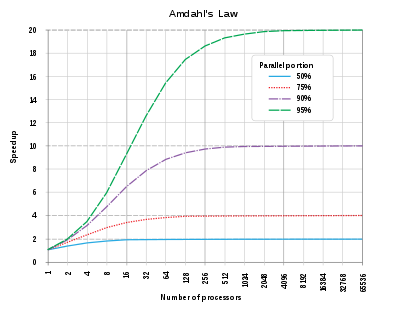
As we can see that in above example that if we increase the total parallel portion of the system the speedup also increases to a certain limit but after that limit the speedup will remain constant, For example for 50% parallel portion the speedup will increase upto 8 processors but after that the speedup will remain constant. In practical a system can't be run parallely 100 perecent because there will always be a task that needs to be executed sequentially.
Derivition
Let us assume for system the p fraction is section initially running in serial but can be executed parallely and reamining section can be only be executed in serial.
so the original execution time will be the sum of time it take to execute the serial and parallel sections.
$T_1$ = (1 - p)T + pT .... (1)
As we know that p fraction can be executed parallely so the time when we run them in n multiple processors be
$T_n$ = $(1 - p)T + \frac{p}{n}T$ .... (2)
and we already know that
speedup = $\frac{T_{1}}{T_{p}}$ .... (3)
putting (1), (2) in (3), we get
speedup = $\frac{(1 - p)T + pT}{(1 - p)T + \frac{p}{n}T}$
solving equation we will get
speedup = $\frac{1}{(1 - p) + \frac{p}{n}}$
Examples
55% of program's execution time occurs inside a loop that can be executed in parallel and rest 45% in serial. What is maximum speedup we should expect from a parallel version of the program executing on 4 CPUs?
Given:
parallel part => p = 0.55
serial part => 1 - p = 0.45
processors => n = 4
speedup = $\frac{1}{0.45 + \frac{0.55}{4}}$
$speedup \approx 1.70$
It means the maximum speedup you should expect from a parallel version of the program executing on 4 CPUs is approximately 1.70 times faster than the serial version.
Advantages
- Helps us understand the limits of parallelization in programs.
- Efficient resource allocation in parallel computing.
- Helps identify bottlenecks.
- Calculates maximum speedup that can be achiveved by parallelizing a program.
- Helps in system design.
Disadvatages
- Assumes fixed problem size and overlooks dynamic workloads
- No Real-world scenarios taken in accunt.
- Efficiency decreases when the number of processors increases.
