Applications of Catalan Numbers

In this article, we have explored different applications of Catalan Numbers such as:

• number of valid parenthesis expressions
• number of rooted binary trees with n internal nodes
• number of ways are there to cut an (n+2)-gon into n triangles
• How many “mountain ranges” can you form with n upstrokes and n downstrokes
• How many paths are there of length 2n that lead from the upper left corner to the lower right corner
• Number of ways to tile a stairstep shape of height n with n rectangles
• number of Binary search trees that can be constructed with n nodes
• Dyck paths

and many more.

Before going into the applications, we have covered the basic details of Catalan numbers followed by 3 algorithmic techniques to calculate it.

What are Catalan Numbers?

The Catalan numbers are a sequence of positive integers that appear in many counting problems in combinatorics. They count certain types of lattice paths, permutations, binary trees, and many other combinatorial objects. They satisfy a fundamental recurrence relation, and have a closed-form formula in terms of binomial coefficients

The first few Catalan numbers for n = 0, 1, 2, 3, … are 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862.

Intuition behind Catalan Numbers

Suppose m = a+b where a=b, votes were cast in an election, with candidate A receiving a votes and candidate B receiving b votes. The ballots are counted individually in some random order, giving rise to a sequence of a As and b Bs.
Assuming all such sequences are equally likely, in how many such sequences can candidate A led throughout the counting of the ballots?

Another way of asking this would be if every vote for A is considered as +1 and every vote for B is a -1, in how many ways can the votes be counted so that the sum while counting is always non negative?

Of course since there are an equal number of +1s and -1s the sum at the end will be 0 but we want the sum during the counting to be non negative.

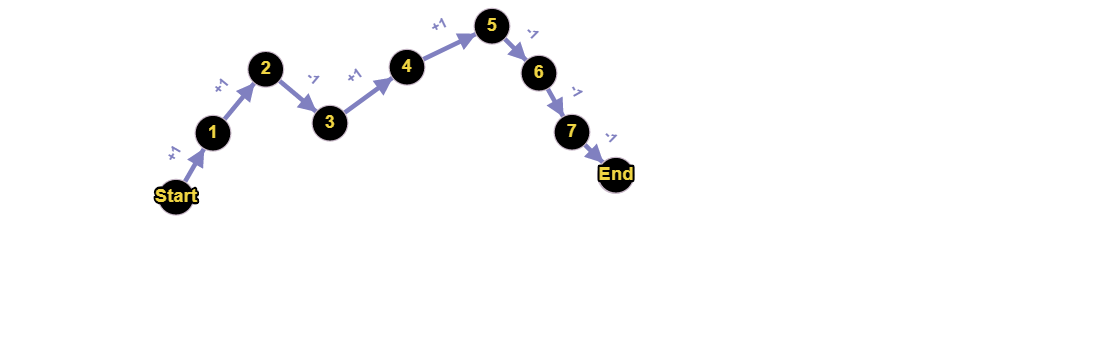
This is therefore equivalent to asking how many such non negative paths exists from the first node to the last node considering a=b. This is where it gets interesting.

If we take a close look at the graph formed we realise that the first number in the sequence should be +1 and the last should be -1 as the total sum is zero and the number of non neagtive paths is equivalent to the number of combinations of nodes excluding first and last node.

Hence the number of non negative paths is in fact the n^th catalan number,where n is number of nodes between the first and last nodes.

Hence from this example we get an idea of how catalan number effectively solves any real life problems.

Calculation of Catalan Numbers:

1. Recursive Approach: Below is the recursive function to find nth catalan number.
   Time Complexity: Time complexity of thsi implementation is equivalent to nth catalan number.Since the n^th catalan number is exponential hence time complexity is also exponential.

long long int catalan(int n) 
{ 
     
    if (n <= 1) return 1; 
  
    
    long long int ans = 0; 
    for (int i=0; i<n; i++) 
        ans += catalan(i)*catalan(n-i-1); 
  
    return ans; 
}

2. Dynamic Programming Solution :It is quite evident that a larger problem can be subdivided into numerous subproblems hence a dp solution also exits for the same.
   Time Complexity of this approach :O(n²)

long long int catalan(int n) 
{ 
     
    if (n <= 1) return 1; 
   long long int dp[n+1];
    dp[0]=dp[1]=1;
    long long int ans = 0; 
    
    for(int i=2;i<=n;i++)
    {
    for(int k=0;k<i;k++)
    {
    dp[i]=dp[j]*dp[i-j-1];
    }
    }
  
    return dp[n]; 
}

3. Using Binomial Coefficient:Catalan numbers can also be represented as Catalan(n)=²ⁿC_n/(n+1).
   This reduces the time complexity to:O(n).

long long int binomialCoeff(int n,int k) 
{ 
    long long int ans = 1; 
 
    for (int i = 0; i < k; ++i) 
    { 
        ans *= (n - i); 
        ans /= (i + 1); 
    } 
   return ans; 
} 
  

long long int catalan(int n) 
{ 
    
    long long int res = binomialCoeff(2*n, n); 
    return c/(n+1); 
} 
  

Some Other Applications of Catalan Numbers:

1. The number of valid parenthesis expressions that consist of n right parentheses and n left parentheses is equal to the n^th Catalan number.
   For example for n=3 we have ()()(), ()(()), (())(), (()()) and ((())).

2. A rooted binary tree is a tree with one root node, where each node has either zero or two branches descending from it. A node is internal if it has two nodes coming from it. The number of rooted binary trees with n internal nodes is in fact the n^th catalan number.
   

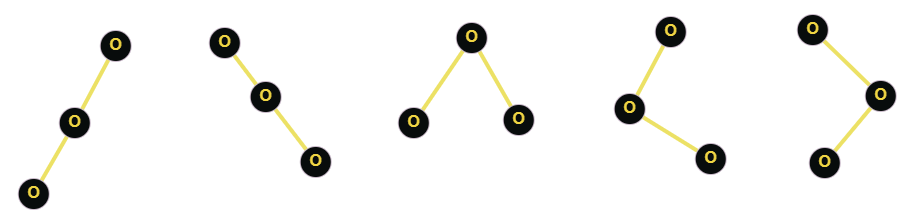
3. The number of ways are there to cut an (n+2)-gon into n triangles, by drawing n-1 non-crossing lines between vertices of the polygon.

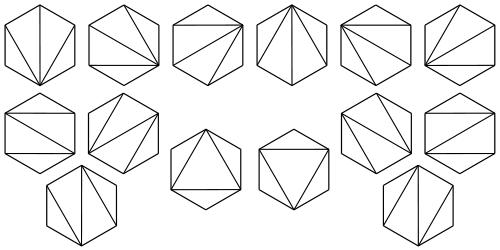
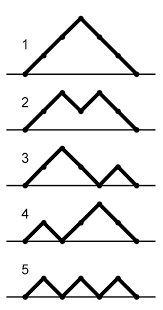
4. How many “mountain ranges” can you form with n upstrokes and n downstrokes that all stay above the original line?
   

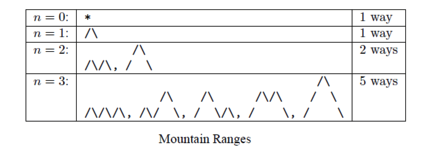
5. In a grid of n×n squares, how many paths are there of length 2n that lead from the upper left corner to the lower right corner that do not touch the diagonal dotted line from upper left to lower right? In other words, how many paths stay on or above the main diagonal?
   Just rotate the previous image and you get this
   

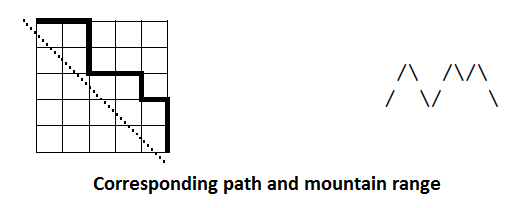
6. Number of ways to tile a stairstep shape of height n with n rectangles. The following figure illustrates the case n = 4:

7. The number of Binary search trees that can be constructed with n nodes is n^th catalan number.
   

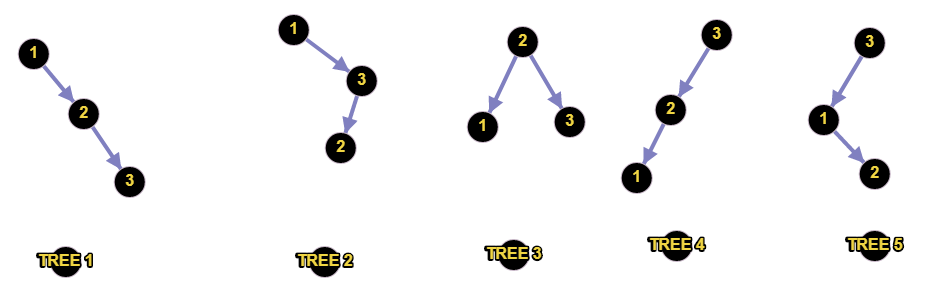
8. Some sequences also describe Dyck paths of length 2n, which are sequences of equally-spaced northeast and southeast walks starting at the origin, ending on the xx-axis, and never going below the x-axis. The bijection between acceptable sequences and Dyck paths assigns a +1 to a northeast walk and a -1 to a southeast walk, and the acceptability condition is equivalent to the path never dropping below the starting and finishing line.
   for n=3 the following 5 paths are possible:
   

Question

An interesting question would be to count how many times you have to go through the inner loop, i.e. count how many times you print "hello world", in:
for i₁= 0 to 1
for i₂= i₁ to 2
for i₃= i₂ to 3
.
.
.
for i_n= i_n-1 to n
print("hello world")

Hint:(Think of catalan numbers!)

With this article at OpenGenus, you must have the complete idea of different applications of Catalan Numbers. Enjoy.