Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 25 minutes | Coding time: 40 minutes
In this article, we have explored how to implement Binary Tree Data Structure in C++ including all different operations like traversing, inserting and deleting. We have used Object Oriented Programming (OOP) concepts.
What is a Binary tree? (general form)
A Binary tree is a heirarchichal data structure in which every node has 2 children, also known as left child and right child, as each node has 2 children hence the name "Binary".
Root node is the topmost node of the tree.
Binary Tree representation:
1. Sequential representation:
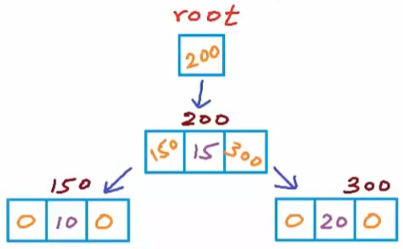
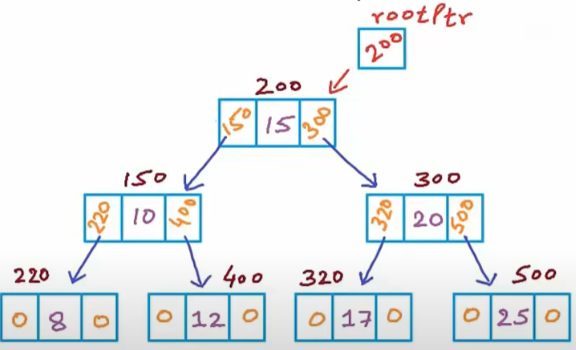
In this representation, array structure is used to implement the tree. Size of array is equal to the total nodes in the tree, index of root node is 0. If a node is at 'i' location then its left child is at '2i' index and right child at '2i + 1' location in the array. Visual Representation:

Linked-list Representation:
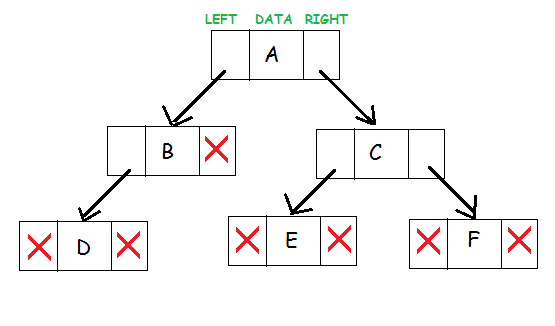
As you can see, the topmost node is the parent node of nodes "B" and "C". Each node contains a pointer to the left subtree and pointer to the right subtree. Node A has a pointer to the left child that is B and a pointer pointing to the right child of A that is B. Middle box represents the data in the node. The nodes which doesn't have a child are called ass leaf nodes. These nodes do not have pointer to their subtrees. Therefore left and right pointers are set to NULL.
To implement binary tree, we will define the conditions for new data to enter into our tree.
Binary Search Tree Properties:
The left sub tree of a node only contain nodes less than the parent node's key.
The right sub tree of a node only contains nodes greter than the parent node's key.
To learn more about Binary Tree, go through these articles:
We will now a implement Binary tree using Linked list representation.
We will use a class to declare a single node and use it to declare linked list of nodes.
#include<iostream>
using namespace std;
class BSTNode
{
public:
int Key;
BSTNode * Left;
BSTNode * Right;
BSTNode * Parent;
};
When we want to declare a group of data whether of similar or different data types. We classes in cpp. Declared using 'class' keyword. Our class is "BSTNode" containing a pointer to left and pointer to right.
BSTNode *left; is pointer to Node. Stores the address of left child. and similarly for right. int data declares data of int type.
Nodes will be created in heap using malloc function in c and new functionin c++ and returns a pointer to the object created in . Its important to understand the concepts of stack and memory, heaps in dynamic allocation.
For linked list we keep the information of address of the head node. We can access al other links using head node using links. In this case we know the address of the root node, which is must, without this we won't be able to access the tree using links. To declare the tree we will first need to create a pointer to Node that will store address of root node by : BSTNode* root. Our tree does not have any data yet, so let us assign our root node as NULL. BSTNode* root = NULL.
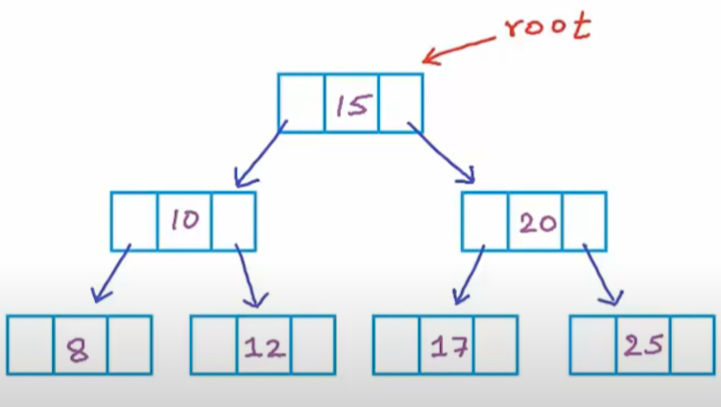
As seen, we are assigning the left and right cells of nodes as addresses to their child and middle cell is for data. Identity of tree is address of the root node, and we have declared a pointer to node in which we are storing address of root node. For empty tree root pointer should be set as NULL. Consider this rootPtr as a different box pointing towards different nodes in our tree, and for pointing to different nodes we have to pass the address of the nodes.
In the beginning it is not pointing towards any node and therfore NULL value. As we progressively add more nodes we'll change the address in this rootptr to point towards specific node in which we have to add the data.
int main() {
BSTNode* root = NULL; // Creating an empty tree
"BSTNode* newNode=new BSTNode();" Returns the address of newly created node which we are collecting in variable newNode of type 'pointer to BSTNode' because we can access heap memory using pointers. This variable now has structure of a doubly linked list in which data is assigned to data variable of 'newNode' and setting left and right child of 'newNode' as NULL then we are returning address of 'newNode' itself.
Well, now our tree is empty, we have no data. Let's insert new data into our tree. For this we will call and define 'Insert' function. Firstly we'd have to call it in our main function as:
int main() {
BSTNode* root = NULL; // Creating an empty tree
root = Insert(root, 15);
root = Insert(root, 10);
root = Insert(root, 20);
Now let us define Insert function which is taking 2 arguments as "root" and new integer data to be inserted in our tree as follows:
BSTNode * BST::Insert(BSTNode * node, int key)
{
// If BST doesn't exist
// create a new node as root
// or it's reached when
// there's no any child node
// so we can insert a new node here
if(node == NULL)
{
node = new BSTNode;
node->Key = key;
node->Left = NULL;
node->Right = NULL;
node->Parent = NULL;
}
// If the given key is greater than
// node's key then go to right subtree
else if(node->key < key){
node->Right = Insert(node->Right, key);
node->Right->Parent = node;
}
// If the given key is smaller than
// node's key then go to left subtree
else
{
node->Left = Insert(node->Left, key);
node->Left->Parent = node;
}
else if condtion is done when root pointer is not NULL.Converting our code into english:
If the new data is less than the data in our root node then insert that data into its left pointer aka left child of node, and assign that node's parent as root node. Similarly if data is greater than data of root node then insert that integer into its right child and assign its parent as root node.
root->left is the pointer to its left node.
Insert function will again call itself, checks if root is empty, and follows the same procedure. This is a recursive loop.
Setp by step analysis:
Firstly our tree is empty, now we are inserting new integer (15), therfore condition of root == NULL is satisfied and it will call GetNewNode and create newNode and returns its address to variable root. We have now updated our root variable, it is no longer empty, it has address of newly created node. Now we are inserting 10 in our tree which is less than current root data, therfore we are inserting it in root->left, calls Insert again recursively, checks if root == NULL, its satisfied, creates another node and 9 is inserted into the left child of our root node.
When we create new node we assign its left and right pointer to NULL as empty.
In this way through recursion it will keep inserting new data into our binary tree. Updated tree is as follows:
Whole code is as-
#include<iostream>
using namespace std;
class BSTNode
{
public:
int Key;
BSTNode * Left;
BSTNode * Right;
BSTNode * Parent;
};
// Function to create a new Node in heap
BSTNode * BST::Insert(BSTNode * node, int key)
{
// If BST doesn't exist
// create a new node as root
// or it's reached when
// there's no any child node
// so we can insert a new node here
if(node == NULL)
{
node = new BSTNode;
node->Key = key;
node->Left = NULL;
node->Right = NULL;
node->Parent = NULL;
}
// If the given key is greater than
// node's key then go to right subtree
else if(node->key < key){
node->Right = Insert(node->Right, key);
node->Right->Parent = node;
}
// If the given key is smaller than
// node's key then go to left subtree
else
{
node->Left = Insert(node->Left, key);
node->Left->Parent = node;
}
int main() {
BSTNode* root = NULL; // Creating an empty tree
/*Code to test the logic*/
void BST::Insert(int key){
root = Insert(root,15);
root = Insert(root,10);
root = Insert(root,20);
root = Insert(root,25);
root = Insert(root,8);
root = Insert(root,12);
}
Operations on Binary tree:
Now, we have succefully reated a new Binary search tree and can insert new keys in it. Now, we want to traverse the tree PREorder. We will implement a function called printInOrder which traverses our tree from its root node, then travserse it left subtree, and then right subtree.
1. Pre order Traversal
For eg-
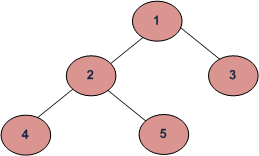
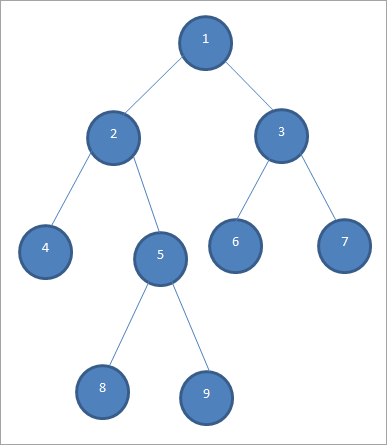
PREorder (Root, Left, Right) : 1 2 4 5 3
Our Alogirthm for traversing PREorder is: we will use recursion.
- Visit root.
- Traverse the left subtree, call printPREorder(left-subtree).
- Traverse the right subtree, call printPREOrder(right-subtree).
For printing visiting root or printing root node first we will make changes in main function to print root node first, then call printPREOrder(root) later.
Defining printPREOrder function as follows:-
void BST::printPREOrder(BSTNode * node){
// Stop printing if no node found
if (node == NULL)
return;
/* first print data of node */
printf("%d ", node->data);
/* then recur on left subtree */
printPreorder(node->left);
/* now recur on right subtree */
printPreorder(node->right);
}
2. Searching a key in the Tree:
Finding out if key exists or not in our tree. We will compare the key with current node, if key is less than current node then search the left subtree otherwise search right subtree. Then again compare the key with current node till found. This is a recursive function.
BSTNode * BST::Search(BSTNode * node, int key)
{
// The given key is
// not found in BST
if (node == NULL)
return NULL;
// The given key is found
else if(node->key == key)
return node;
// The given is greater than
// current node's key
else if(node->key < key){
return Search(node->right, key)
}
// The given is smaller than
// current node's key
else
return Search(node->left, key);
}
3. Finding minimum and maximum values in Binary tree:
It is pretty easy to find max and minimum data in Binary Search Tree. To get minimum value we just have get the leftmost value in our tree and to get maximum value we just have to get the rightmost value in the tree.
int BST::FindMin(BSTNode * node)
{
if(node == NULL)
return -1;
else if(node->Left == NULL)
return node->Key;
else
return FindMin(node->Left);
}
int BST::FindMax(BSTNode * node)
{
if(node == NULL)
return -1;
else if(node->Right == NULL)
return node->Key;
else
return FindMax(node->Right);
}
Return -1 if we dont find maximum or minimum value in our tree.
4. Removing or deleting a node from the tree
There are 3 possible cases for removing the node from the tree which are as follows-
- Removing the leaf node is the easiest case of the three. We just have to remove the node which does not have any child. In our tree, leaf nodes are- 8, 12, 17, 25
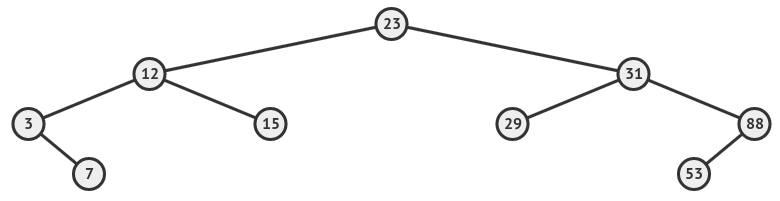
- If the removed node has one child (either left or right). After deleting the node we just have to point the address of parent node to the child node of the deleted one. for eg, in above tree, nodes 88 and 3 have a single node. If we want to remove node 88 then we have to point parent node of 53 to 31 and make right node of 31 as 53.
- Removing the node with 2 children. If our node has 2 children then first find out the successor or predecessor of that node, then replace that node with successor or predecessor node. For eg if want to removes node 12, then first anyone of the successor or predecessor, let us find predecessor to 12, which is 7 then replace 12 with 7. Now, 7 has 15 and 3 as its children. As we can choose anyone of the successor or predecessor we could have 2 binary tree representations after deletion of a node.
For this case we first have to define predecessor and successor of a node.
4.1) Finding the Successor of a key
Successor is the immediate number after a particular key.
If we want to find successor of a particular key, let's say "T", then successor will be minimum key in the right subtree of T. Our minimum function could be useful here. We will find minimum key in the right subtree of T.
int BST::Successor(BSTNode * node)
{
// The successor is the minimum key value
// of right subtree
if (node->Right != NULL)
{
return FindMin(node->Right);
}
}
4.2 Finding predeccessor of T
Predecessor is the key coming just before T. We will use maximum function thhat we have already defined. Find the maximum value in the left subtree of T.
int BST::Predecessor(BSTNode * node)
{
// The predecessor is the maximum key value
// of left subtree
if (node->Left != NULL)
{
return FindMax(node->Left);
}
}
Removing a key from our Tree
There exist 3 cases for removing a node which are-
- Remove a node having no child that is a node with node->left = NULL and node ->right = NULL.
- Remove a node having a single right or a left child.
node->left == NULL && node->right != NULL
node->left != NULL && node->right == NULL
We have to remove the node and connect the child node to the parent node of that deleted node. - Removing a node having 2 children. We could replace the target node to be deleted with its successor or predecessor. for eg, if our target node to be deleted is 12 which has 2 children then we have two options, either replace 12 with its predecessor (7) or replace it with its successor (15). Following is the code taking into consideration above 3 cases.
BSTNode * BST::Remove(BSTNode * node,int key)
{
node = BST::Search(node, int key)
// The given node is
// not found in BST
if (node == NULL)
return NULL;
// Target node is found
if (node->Key == key)
{
// If the node is a leaf node. The node can be safely removed
if (node->Left == NULL && node->Right == NULL)
node = NULL;
// The node have only one child at right
else if (node->Left == NULL && node->Right != NULL)
{
// The only child will be connected to the parent's of node directly
node->Right->Parent = node->Parent;
Copy
// Bypass node
node = node->Right;
}
// The node have only one child at left
else if (node->Left != NULL && node->Right == NULL)
{
// The only child will be connected to
// the parent's of node directly
node->Left->Parent = node->Parent;
Copy
// Bypass node
node = node->Left;
}
// The node have two children (left and right)
else
{
// Find successor or predecessor to avoid quarrel
int successorKey = BST::Successor(key);
// Replace node's key with successor's key
node->Key = successorKey;
Copy
// Delete the old successor's key
node->Right = Remove(node->Right, successorKey);
}
}
// Target node's key is smaller than
// the given key then search to right
else if (node->Key Right = Remove(node->Right, key);
// Target node's key is greater than
// the given key then search to left
else
node->Left = Remove(node->Left, key);
// Return the updated BST
return node;
int main() {
BSTNode* root = NULL; // Creating an empty tree
/*Code to test the logic*/
void BST::Insert(int key){
root = Insert(root,15);
root = Insert(root,10);
root = Insert(root,20);
root = Insert(root,25);
root = Insert(root,8);
root = Insert(root,12);
}
//Print in Preorder
void BST::printPREOrder(){
printPREOrder(root);
}
//For searching a aprticular key in tree
bool BST::Search(int key)
{
// Invoking Search() operation
// and passing root node
BSTNode * result = Search(root, key);
// If key is found, returns TRUE
// otherwise returns FALSE
return result == NULL ?
false :
true;
}
//To find minimum or maximum we xan invoke those functions as:
int BST::FindMin()
{
return FindMin(root);
}
int BST::FindMax()
{
return FindMax(root);
}
//To remove a key we would always start from root key
void BST::Remove(int key)
{
root = Remove(root, key);
}
}
With this article at OpenGenus, you must have the complete idea of implementing Binary Tree in C++. Enjoy.
Learn more: